Повторить основные методы решения квадратных, рациональных и иррациональных уравнений.
Квадратные уравнения. Рациональные уравнения. Иррациональные уравнения
Напомним, что уравнением называется равенство двух выражений с одной или несколькими переменными.
Уравнение с одной переменной имеет вид:
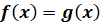 ,
,
где 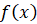 ,
,  – некоторые функции переменной
– некоторые функции переменной  .
.
Корнем (решением) уравнения с одной переменной называется число 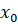 , при подстановке которого вместо
, при подстановке которого вместо  в обе части уравнения получается верное числовое равенство.
в обе части уравнения получается верное числовое равенство.
Решить уравнение – значит найти все его кони или доказать, что корней нет.
Множество значений переменной  , при которых определены функции
, при которых определены функции 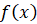 и
и  , называется областью определения уравнения или областью допустимых значений переменной (ОДЗ).
, называется областью определения уравнения или областью допустимых значений переменной (ОДЗ).
Уравнения, имеющие одни и те же корни, называются равносильными. Уравнения, не имеющие корней, также считаются равносильными.
Теоремы о равносильности уравнений:
1.  .
.
2.  для любого числа
для любого числа  .
.
3.  для любого числа
для любого числа 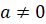 .
.
4.  , если
, если  имеет смысл в области определения уравнения.
имеет смысл в области определения уравнения.
5.  , если
, если  определена
определена
и не обращается в нуль в области определения уравнения.
6.  .
.
7. 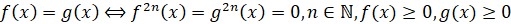 .
.
Напомним, что уравнение вида 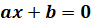 , где
, где  и
и  , называется линейным. Число корней уравнения зависит от значений
, называется линейным. Число корней уравнения зависит от значений  и
и  .
.
Линейное уравнение при  имеет единственное решение
имеет единственное решение  ;
;
при  ,
,  – не имеет решений;
– не имеет решений;
при  ,
, 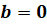 – принимает вид
– принимает вид 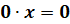 и имеет бесконечное множество решений.
и имеет бесконечное множество решений.
Давайте решим следующее уравнение  .
.
Решение.

А теперь давайте поговорим о квадратных уравнениях. Напомним, что квадратным уравнением называется уравнение вида:
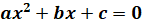 ,
,
где  – переменная,
– переменная,  ,
,  ,
,  , причём
, причём 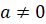 .
.
Число корней квадратного уравнения зависит от значения дискриминанта, который вычисляется по формуле:  .
.
Если 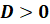 , то уравнение имеет два различных действительных корня:
, то уравнение имеет два различных действительных корня:
 .
.
Если  , то уравнение имеет два равных действительных корня:
, то уравнение имеет два равных действительных корня:
 .
.
Если 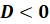 , то уравнение не имеет корней.
, то уравнение не имеет корней.
Уравнение вида  , где
, где 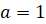 , называется приведённым квадратным уравнением.
, называется приведённым квадратным уравнением.
Уравнения вида 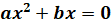 ,
,  ,
,  называются неполными квадратными уравнениями.
называются неполными квадратными уравнениями.
Неполные квадратные уравнения обычно решаются без применения общей формулы.
В уравнении 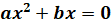 (
(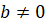 ,
, 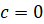 ) левая часть раскладывается на множители:
) левая часть раскладывается на множители:
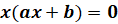 , откуда
, откуда  ,
,  .
.
Уравнение  (
( ) не имеет корней, если знаки
) не имеет корней, если знаки  и
и  совпадают;
совпадают;
имеют два корня: 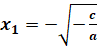 ,
,  , если знаки
, если знаки  и
и  различны.
различны.
Уравнение  имеет два равных корня:
имеет два равных корня:  .
.
Важное значение при решении и исследовании квадратных уравнений имеет теорема Виета. Вспомним её.
Итак, теорема Виета (прямая):
если квадратное уравнение 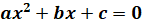 имеет корни,
имеет корни,
то  .
.
Для корней приведённого квадратного уравнения 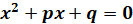 формулы Виета имеют следующий вид:
формулы Виета имеют следующий вид:
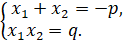
Теорема Виета (обратная):
если сумма каких-нибудь чисел 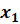 и
и  равна
равна  , а их произведение равно
, а их произведение равно  , то эти числа являются корнями квадратного уравнения
, то эти числа являются корнями квадратного уравнения 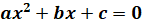 .
.
Если дискриминант квадратного трёхчлена  положителен, то трёхчлен можно представить в виде
положителен, то трёхчлен можно представить в виде 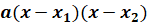 , где
, где 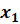 ,
,  – корни уравнения
– корни уравнения 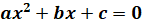 .
.
Если дискриминант квадратного трёхчлена  э равен нулю, то трёхчлен можно представить в виде
э равен нулю, то трёхчлен можно представить в виде 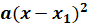 , где
, где 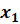 – корень уравнения
– корень уравнения 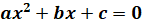 .
.
Решим следующее уравнение 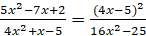 .
.
Решение.


Перейдём к рациональным уравнениям. Напомним, что функция вида
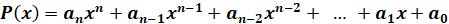 ,
,
где 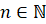 ,
,  ,
, 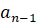 ,
, 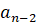 , …,
, …,  ,
,  – некоторые действительные числа, называется целой рациональной функцией.
– некоторые действительные числа, называется целой рациональной функцией.
Целым рациональным уравнением называется уравнение вида 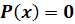 , где
, где  – целая рациональная функция.
– целая рациональная функция.
Дробно-рациональным уравнением называется уравнение вида 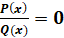 , где
, где  и
и  – многочлены.
– многочлены.
При решении рациональных уравнений используются метод разложения на множители и метод замены.
Решим следующее уравнение 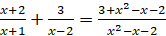 .
.
Решение.
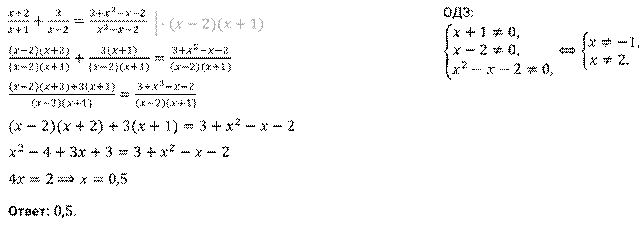
Также напомним, что иррациональным уравнением называется уравнение, в котором переменная содержится под знаком корня или под знаком операции возведения в дробную степень.
Основные методы решения иррациональных уравнений:
1. Возведение обеих частей уравнения в одну и ту же степень.
2. Замена переменной.
3. Умножение обеих частей уравнения на одну и ту же функцию.
4. Применение свойств функций, входящих в уравнение.
Решим следующее уравнение 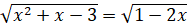 .
.
Решени е.
