Лекция №3.
Тема: Матрицы. Определитель.
Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов:
.
Строки и столбцы нумеруются, начиная слева сверху. Когда говорят: матрица размером m n (или m на n), подразумевают под m количество строк, а под n количество столбцов. Например, матрица на рисунке 1-1 имеет размер "4 на 3", а не "3 на 4".
Если число строк матрицы не равно числу столбов (m≠n), то матрица называется прямоугольной
.
Если число строк равно числу столбцов (m=n), то матрица называется квадратной
.
Число строк или столбцов квадратной матрицы называется ее порядком.
.
Определение.
Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний угол.
Определение.
Побочной диагональю матрицы называется диагональ, проведённая из левого нижнего угла матрицы в правый верхнийугол.
Главная диагональ - на ней номера строк и столбцов одинаковые. Идёт она слева направо сверху вниз.
Определение.
Строка матрицы называется нулевой, если все ее элементы равны нулю.
Определение.
Столбец матрицы называется нулевым, если все его элементы равны нулю
Матрица, все элементы которой равны нулю называется нулевой и обозначается так:
.
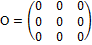Квадратная матрица, в которой отличны от нуля только элементы, находящиеся на главной диагонали, называются диагональными
.
Если в диагональной матрице все числа главной диагонали равны между собой, то матрица называется скалярной. Если в скалярной матрице все числа главной диагонали равны единице, то матрица называется единичной и обозначается буквой Е
|
|
.
В прямоугольной матрице типа m х n возможен случай, когда m=1 или n=1, при этом получается матрица-строка или матрица-столбец, такие матрицы называют векторами ( вектор-столбец, вектор-строка ):
.
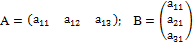Две матрицы называются равными, если они имеют одинаковое число строк m и одинаковое число столбцов n и их соответствующие элементы равны.
Если в матрице типа m х n переставить строки со столбцами, получим матрицу типа n х m, которую будем называть транспонированной матрицей:
.
Свойства транспонированных матриц:
- Если матрица A имеет размер n×m, то транспонированная матрица AT имеет размер m×n;
- (AT)T = A;
- (k · A)T = k · AT;
- (A + B)T = AT + BT;
- (A · B)T = BT · AT.
Суммой матриц А и В условимся называть такую матрицу, элементы которой равны сумме соответствующих элементов матриц А и В. Складывать можно только матрицы, имеющие одинаковое строение.
Свойства сложения:
ü А+В=В+А
ü (А+В)+С=А+(В+С)
Произведением матрицы А на число k называется такая матрица kА, каждый элемент которой равен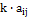 
. Умножение матрицы на число сводиться к умножению на это число всех элементов матрицы.
Для операций над матрицами и числами справедливы свойства: (обозначим числа буквами x и y, а матрицы буквами A и B)
Ø x(yA)=(xy)A
Ø x(A+B)=xA+xB
Ø (x+y)A=xA+yA
Произведением квадратных матриц
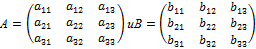
называется матрица
= 
.
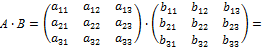
| Первая строка * первый столбец | Первая строка * второй столбец | Первая строка * третий столбец |
| Вторая строка * первый столбец | Вторая строка * второй столбец | Вторая строка * третий столбец |
| Третья строка * первый столбец | Третья строка * второй столбец | Третья строка * третий столбец |
Правила умножения прямоугольных матриц:
|
|
ü умножение матрицы А на матрицу В имеет смысл только в том случае, когда число столбцов матрицы А равно числу строк матрицы В;
ü в результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк в первой матрице, и столько столбцов, сколько столбцов во второй матрице.
Свойства умножения матриц:
А∙В ≠ В∙А
А(ВС)=(АВ)С
(А+В)С=АС+ВС