Достаточное условие монотонности функции даёт теорема 1§3, то есть если функция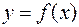 
дифференцируемая, то решая неравенства 
и 
, найдём интервалы монотонности функции. Теорема Ферма даёт необходимое условие экстремума для дифференцируемой функции.
Заметим, что функция, непрерывная в точке 
, но не дифференцируемая в ней, может достигать экстремума. Например, функции 
достигают в точке 
минимума, но не дифференцируемые в этой точке. Даже разрывная в точке функция может достигать в этой точке экстремума. Например, функция
достигает в нуле максимума (см. рис.).
Из теоремы Ферма и приведённых примеров следует, что точки, в которых производная обращается в нуль или не существует (их называют критическими), – это точки возможного экстремума. Чтобы убедиться, достигается ли на самом деле в этих точках экстремум, следует воспользоваться достаточным условием.
Теорема 1 (достаточное условие экстремума для непрерывной функции). Пусть функция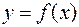 
непрерывна в точке 
, дифференцируема в некоторой окрестности этой точки за исключением, быть может, самой точки . Тогда если при переходе через точку слева направо знак производной 
: а) меняется с + на –, то функция достигает в точке максимума; б) меняется с – на + – минимума; в) не меняется – экстремума нет.
Доказательство. Пусть 
или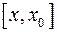 
– произвольный отрезок из окрестности точки . Функция 
удовлетворяет условию теоремы Лагранжа на этих отрезках, то есть
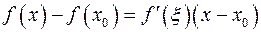, (1)
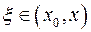или 
.
Рассмотрим случай а). Если 
, то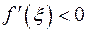 
и правая часть (1) отрицательна, то есть 
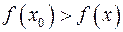. Если 
, то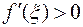 
и снова правая часть (1) отрицательная, то есть 
. Итак, для любого 
из окрестности точки имеем , что означает максимум в точке . Случай а) доказан. Случаи б) и в) доказываются аналогично. Теорема доказана.
Пример 1. Найти интервалы монотонности и экстремум функции 
.
Решение. Функция определена и непрерывна на всей числовой оси. Найдём критические точки
– критические точки. Они разбивают область определения функции на три интервала: 
, (см. рис.).
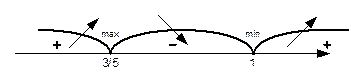
При этом производная положительна на первом и третьем интервале, а отрицательна на втором. Следовательно, функция 
возрастает на интервалах 
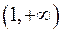и убывает на интервале 
.
Так как в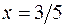 
меняет знак с + на –, то, согласно теореме 1, в этой точке достигает максимума, 
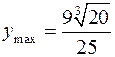. Аналогично в точке 
– минимума, 
.
Если функция 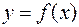дважды дифференцируема в критической точке, то можно дать второй достаточный признак существования экстремума.
Теорема 2. Если функция 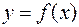имеет в некоторой окрестности точки вторую производную, а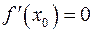 
, то 
достигает в точке максимума, если 
. Достигает минимума, если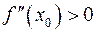 
.
Доказательство. Из существования 
следует непрерывность 
и 
в окрестности точки . Пусть 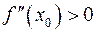, тогда функция возрастает в окрестности точки . Поскольку 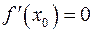, то 
меняет знак с – на +. А это, согласно теореме 1, означает минимум функции в точке . Аналогично доказывается случай, когда . Теорема доказана.
Пример 2. Убедиться, что функция примера 1 достигает в точке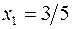 
максимума.
Решение. 
.
Замечание. Если 
, то для выяснения существует ли экстремум можно воспользоваться формулой Тейлора:
.
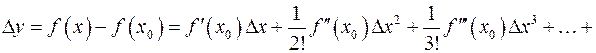
Пример 3. Исследовать на экстремум функцию
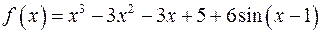
в точке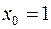 
.
Решение. 
,
,
,
,
.
. (2)
(2) – формула Тейлора.
Если взять достаточно малую окрестность точки 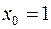, то знак правой части (2) будет определяться только первым слагаемым. Но его знак не сохраняется ни в какой окрестности точки 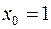. Следовательно, функция не имеет экстремума в точке .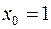