На наклонной плоскости с углом наклона 
к неподвижной стенке прикреплена пружина с грузом 
массой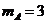 
кг. Коэффициент жесткости пружины 
, длина нерастянутой пружины 
. В начальный момент времени 
груз находится в покое. Затем к грузу прикрепляют груз 
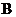массой 
кг. Необходимо найти законы движения грузов:
a)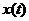 
, взяв за начало отсчёта положение грузов при нерастянутой пружине – точку 
,
б) 
взяв за начало отсчёта положение равновесия скреплённых грузов и 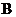, точку 
.
Трением пренебречь. Грузы считать материальными точками.
Рис. 3.1
Решение
Запишем второй закон Ньютона для скреплённых грузов. При этом грузы и 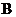будем считать материальной точкой с массой
На грузы действуют сила тяжести 
, сила упругости пружины F и сила нормальной реакции гладкой наклонной плоскости N. Запишем второй закон Ньютона
(3.1)
и спроектируем его на ось Ox с началом отсчёта в положении грузов при нерастянутой пружине
. (3.2)
Сила упругости пропорциональна удлинению пружины, которое в данном случае равно координате x
. (3.3)
Подставляя (3.3) в (3.2), получаем
. (3.4)
Разделим уравнение (3.4) на массу грузов
(3.5)
и введем круговую частоту колебаний
.
После этого уравнение (3.5) можно переписать в виде
. (3.6)
Это линейное неоднородное уравнение. Его общее решение можно искать в виде суммы общего решения однородного
, (3.7)
и частного решения неоднородного уравнений
. (3.8)
Общее решение однородного уравнения (3.7) имеет вид
, (3.9)
частное решение неоднородного уравнения (3.8) при постоянной правой части можно искать в виде константы
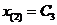. (3.10)
Подставляя (3.10) в (3.8), получим
. (3.11)
Заметим, что частное решение (3.11) соответствует положению равновесия скреплённых грузов A и B. Таким образом, общее решение уравнения (3.6) имеет вид
. (3.12)
Константы C 1, C 2 в уравнении (3.12) зависят от начального положения и скорости грузов.
В свою очередь, начальное положение скреплённых грузов соответствует положению равновесия груза . Запишем уравнение равновесия этого груза с учетом того, что на него действуют силы тяжести 
, упругости пружины F и нормальной реакции N
. (3.13)
Спроектируем уравнение (3.13) на ось Ox
.
Сила упругости пропорциональна удлинению пружины, которое в данном случае равно координате груза в положении равновесия 
. Поэтому последнее уравнение можно переписать в виде
,
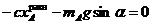и найти
.
Эта координата является начальной координатой скреплённых грузов и 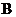при их движении
.
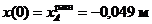Теперь найдём константы C 1, C 2 в уравнении (3.12). Для этого, записав (3.12) и производную от него в начальный момент времени 
, приравняем их к начальной координате и скорости грузов соответственно
,
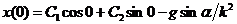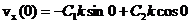(3.14)
Из уравнений (3.14) найдём константы
, 
.
Подставляя найденные константы в уравнение (3.12), окончательно получим
Вычислив численные значения, получаем уравнение движения скреплённых грузов и
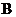
. (3.15)
Закон движения (3.15) грузов записан в системе координат с началом в точке , соответствующей положению грузов, когда пружина не растянута.
Теперь выберем в качестве начала координат точку , соответствующую положению равновесия скреплённых грузов и 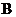. Введём величину λs, соответствующую сжатию пружины в положении статического равновесия (рис. 3.1). Тогда удлинение пружины связано с координатой 
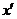следующим образом
,
сила упругости (3.3) имеет вид
,
а проекция второго закона Ньютона на ось –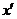
. (3.16)
Если грузы находятся в равновесии, то ускорение и координата 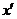равны нулю, отсюда из (3.16) находим
.
Теперь уравнение (3.16) можно переписать в виде
.
Это линейное однородное уравнение имеет известное решение (1.3), константы которого связаны с начальными условиями соотношениями (1.4)
. (3.17)
С учетом того, что начальные координата и скорость равны
, 
,
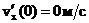получим уравнение движения скреплённых грузов и в системе координат с началом в положении равновесия грузов
.
Заметим в заключении, что этот закон движения отличается от уравнения (3.15) лишь константой, равной статическому удлинению 
, что вполне естественно, поскольку именно это расстояние разделяет начала координат систем отсчета 
и 
.
Список литературы
1. Бутенин Н. В. Курс теоретической механики: учебник для втузов: в 2 т.. Т. 1: Статика и кинематика. Т. 2: Динамика / Бутенин Н. В., Лунц Я. Л., Меркин Д. Р.. - 10-е изд., стер.. - СПб.; М.; Краснодар: Лань, 2008. - 730 с.: ил. ISBN 978-5-8114-0052
2. Тарг С.М. Краткий курс теоретической механики: учебник для втузов / Тарг С. М.. - 20-е изд., стер.. - М.: Высш. шк., 2010. - 416 с.: ил. ISBN 978-5-06-006193-2
3. Яблонский, А. А. Курс теоретической механики: статика, кинематика, динамика: учебник для вузов по техн. спец. / А. А. Яблонский, В. М. Никифорова. - 15-е изд., стер. - М.: КНОРУС, 2010. - 603 с.: ил. ISBN 978-5-390-00352-7: 357.00.
4. Юдин В.А. Лекции по динамике точки /
Юдин В.А. Электронный ресурс. - Новосибирск, 2014.
Составители
Валерий Яковлевич Рудяк
Александр Анатольевич Белкин
Сергей Леонидович Краснолуцкий