Квадратная стальная пластина нагружена равномерно распределенной нагрузкой по всей площади. Границы пластины шарнирно оперты на основание — пластина свободно лежит, опираясь контуром.
Необходимо рассчитать прогибы в разных точках пластины.
Исходные данные:
Наносим на чертеж пластины сетку с шагом a/4. В точках пересечения линий сетки находятся узлы, в которых и будем определять величину прогибов wi (i — номер узла).

Присваиваем номера узлам, начиная с «0».
Номер «0» назначаем всем узлам, расположенным на контуре. Эти узлы по условиям задачи лежат на опорной поверхности и после приложения нагрузки остаются на прежнем месте – прогиб этих узлов равен нулю w0=0.
Из условий приложения и характера нагрузки, а также квадратной формы пластины (условия центральной симметрии) очевидно, что прогиб будет одинаковым во всех узлах «1». Поэтому этим узлам и присвоен одинаковый номер.
Руководствуясь теми же признаками симметрии, назначаем характерным внутренним узлам номер «2».
Понятно, что наибольший прогиб будет в центре пластины, назначаем этому узлу номер «3». Он один, других узлов на пластине, имеющих такой же прогиб нет.
На рисунке вы видите законтурные (зеркальные или мнимые) узлы. Они участвуют в расчете, поэтому нам нужны. Номера им присвоим исходя из простых правил:
1. Если линия контура опирается в этом месте шарнирно, то законтурному (зеркальному) узлу присваивается номер «-N» Где «N» - номер симметричного относительно линии контура внутреннего узла (w—N=-wN).
2. Если контур жестко закреплен (жесткое защемление), то соответствующему зеркальному узлу присваивается номер «N» — такой же, как и симметричному внутреннему узлу (wN=+wN).
Числовые исходные данные о материале и размере пластины, а также о нагрузке записываем в таблицу MS Excel в ячейки D3…D7.

Расчет:
1. В рассматриваемом варианте расчета пластина делится сеткой на 4 квадрата по горизонтали и вертикали. Определяем шаг сетки в мм
в ячейке D9: δ=a/4
2. Цилиндрическую жесткость пластины в Н*мм вычисляем по общеизвестной формуле
в D10: D=(E*h3)/(12*(1- μ2)
3. Для каждого узла, в котором мы хотим найти прогиб, составляем уравнение, применив метод конечных разностей.
Для составления уравнений используем оператор формулы, изображенный выше на схеме пластины.
Мысленно накладываем оператор центральной клеткой сначала на узел «1» и каждой периферийной клеточкой на соответствующие соседние узлы. Пишем уравнение:
20*w1-8*(w0+w2+w3+w2)+2*(w0+w0+w1+w1)+1*(w-1+w0+
w1+w0)=k*q*δ4/D
Думаю, понятно, как оно получилось? Уясните этот шаг, он ключевой при составлении уравнений!
После преобразований получим:
24*w1-16*w2-8*w3=k*q*δ4/D
Выражение в правой части уравнения справедливо для распределенной нагрузки q.
Для сосредоточенной силы F выражение имеет вид: F*δ2/D
Если в точке действуют несколько различных нагрузок, то выражения их характеризующие суммируются в правой части уравнения.
Что такое коэффициент веса k? Если бы распределенная нагрузка была приложена только к центральной части пластины, ограниченной квадратом с узлами «2» по углам, то:
для узлов «2»: k=0,25
для узлов «1»: k=0,5
для узла «3»: k=1
Так как в нашем примере распределенная нагрузка приложена ко всей поверхности пластины, то для всех внутренних узлов k=1.
Накладывая оператор формулы метода конечных разностей последовательно на все уникальные внутренние узлы, нужно составить все уравнения. Из-за равномерности сплошной нагрузки и симметрии формы в нашем примере таких узлов 3, а, следовательно, и уравнений будет тоже 3.
Запишем эти уравнения в таблицу Excel в виде матрицы, заполнив область ячеек O5…Q7.
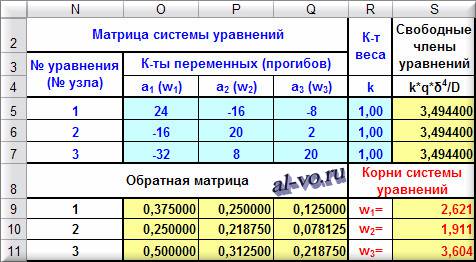
4. Заполним область R5…R7 значениями коэффициентов k.
5. Вычислим свободные члены уравнений в мм
в ячейках S5…S7: k*q*δ4/D
6. Определим коэффициенты обратной матрицы. Для этого впишем формулу массива
в область O9…Q11: {=МОБР(O5:Q7)}
Чтобы правильно ввести формулу массива напишем
в O9: =МОБР(O5:Q7)
Выделим область для обратной матрицы равную по размеру исходной матрице – O9…Q11, нажмем на клавиатуре клавишу F2, затем – Ctrl+Shift+Enter. Excel мгновенно рассчитал коэффициенты обратной матрицы.
7. Для вычисления корней уравнений системы (читай: искомых прогибов) нужно перемножить обратную матрицу с матрицей свободных членов уравнений. Для этого запишем формулу массива
в область ячеек S9…S11: {=МУМНОЖ(O9:Q11;S5:S7)}
Всё, задача решена. Используя метод конечных разностей, мы определили прогибы в узлах «1», «2» и «3». Наибольший прогиб ожидаемо оказался в центре пластины в узле «3».
Ниже приведены скриншоты решения этой же задачи при уменьшенном в 2,5 раза шаге сетки δ. Excel легко решает в этом случае систему из 15-и уравнений!



Что в итоге?
Расчет прогиба в центре пластины из рассмотренного примера по «точным» аналитическим формулам дает следующие результаты при μ=0,3:
wц=0,00406*q*a4/D=3,632 мм (Тимошенко С.П.)
wц=0,0443*q*a4/(E*h3)=3,629 мм (Вайнберг Д.В.)
Прогибы, определенные методом конечных разностей:
При шаге сетки δ=a/4:
wц=w3=3,604 мм (относительная погрешность -0,8%)
При шаге сетки δ=a/10:
wц=w15=3,630 мм (относительная погрешность 0,0%)
Как видим, метод конечных разностей даже при большом шаге сетки дает незначительную погрешность результатов!
Используя рассмотренную методику, можно выполнять расчеты прямоугольных пластин с разными способами закрепления контуров и произвольным расположением распределенных и концентрированных нагрузок. Составление уравнений даже без навыка использования оператора формулы не займет, поверьте, у вас много времени. На вариант с 15-ю узлами было затрачено не более получаса.