Показательные неравенства.
Показательными называются неравенства, содержащие переменную в показателе степени.
Методы решения показательных неравенств такие же, как и при решении показательных уравнений. Однако, нужно помнить, что прежде, чем сравнивать показатели степеней, сначала необходимо сравнить с единицей основание степени.
Решение показательных неравенств основывается на утверждении:
Если  , то неравенство
, то неравенство  равносильно неравенству
равносильно неравенству  Если
Если 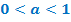 , то показательное неравенство
, то показательное неравенство  равносильно неравенству
равносильно неравенству 
Все показательные неравенства любого уровня сложности, в конечном итоге, сводятся к решению простейших показательных неравенств.
Методы решения показательных неравенств.
1) метод сравнения показателей;
2) метод введения новой переменной;
3) метод разложения на множители;
4) функционально-графический метод;
5) метод почленного деления;
6) метод группировки.
1) Метод сравнения показателей основывается на утверждении, приведённом выше.
Например, 
Т.к. 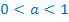 , то функция
, то функция 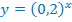 убывающая, значит,
убывающая, значит,


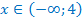
Ответ: 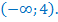
2) Метод введения новой переменной используется для упрощения решения неравенств в тех случаях, когда после всевозможных преобразований получили неравенство, в котором появилась возможность обозначить какую-то степень другой переменной и, при этом, все остальные степени также будут выражаться через введённую переменную.
Обрати внимание! Если в решении неравенства относительно введённой переменной получили двойное неравенство, то, прежде чем переходить к исходной переменной, необходимо записать это двойное неравенство в виде системы двух неравенств, а затем переходить к исходной переменной.
Например, 
Преобразуем неравенство, используя свойства степеней.
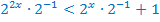
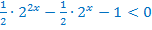
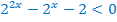
Введём новую переменную: 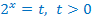 . Тогда неравенство принимает вид:
. Тогда неравенство принимает вид:
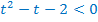
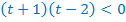
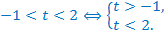
Вернёмся к исходной переменной. Т.к., в силу области значений показательной функции,  при любом значении
при любом значении 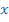 , то осталось решить второе неравенство системы.
, то осталось решить второе неравенство системы.

Основание степени 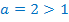 , значит, функция возрастающая, поэтому переходя к сравнению показателей, знак неравенства не меняется.
, значит, функция возрастающая, поэтому переходя к сравнению показателей, знак неравенства не меняется.

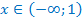
Ответ: 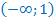
3) Метод разложения на множители используется в тех случаях, когда, после произведённых преобразований, получились степени с одинаковыми основаниями и одинаковыми коэффициентами перед переменной в показателе степени.
Например, 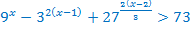
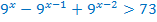
Вынесем за скобки одинаковый множитель, т.е. степень с наименьшим показателем.
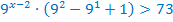

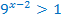

Т.к. 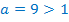 , то показательная функция возрастающая, значит, переходя к сравнению показателей, знак неравенства не меняется.
, то показательная функция возрастающая, значит, переходя к сравнению показателей, знак неравенства не меняется.
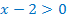

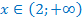
Ответ: 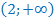
4) Функционально-графический метод обычно используется при решении неравенств смешанного типа, т.е. когда в записи неравенства присутствуют разные функции. При решении таких неравенств следует рассмотреть две функции, построить их графики в одной системе координат, и выяснить, при каких значениях переменной значения одной функции больше (меньше) значений другой функции. Найденные значения аргумента и есть решение неравенства.
Например, 1). Графический метод: 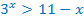
Рассмотрим функции 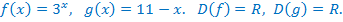
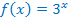 – показательная функция, график её проходит через точку
– показательная функция, график её проходит через точку 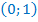 , возрастает, т.к.
, возрастает, т.к. 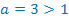 , дополнительные точки
, дополнительные точки 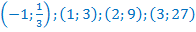 .
.
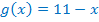 – линейная функция, графиком её является прямая, проходящая через точки
– линейная функция, графиком её является прямая, проходящая через точки 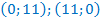 .
.
Построим в одной системе координат графики этих функций. Они пересекаются в точке с абсциссой 2. По графику определяем, что при 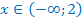 значения линейной функции превышают значения показательной функции (при одних и тех же значениях аргумента) т.е.
значения линейной функции превышают значения показательной функции (при одних и тех же значениях аргумента) т.е.  , а при
, а при 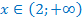 - наоборот, значения показательной функции превышают значения линейной функции, т.е.
- наоборот, значения показательной функции превышают значения линейной функции, т.е.  .
.
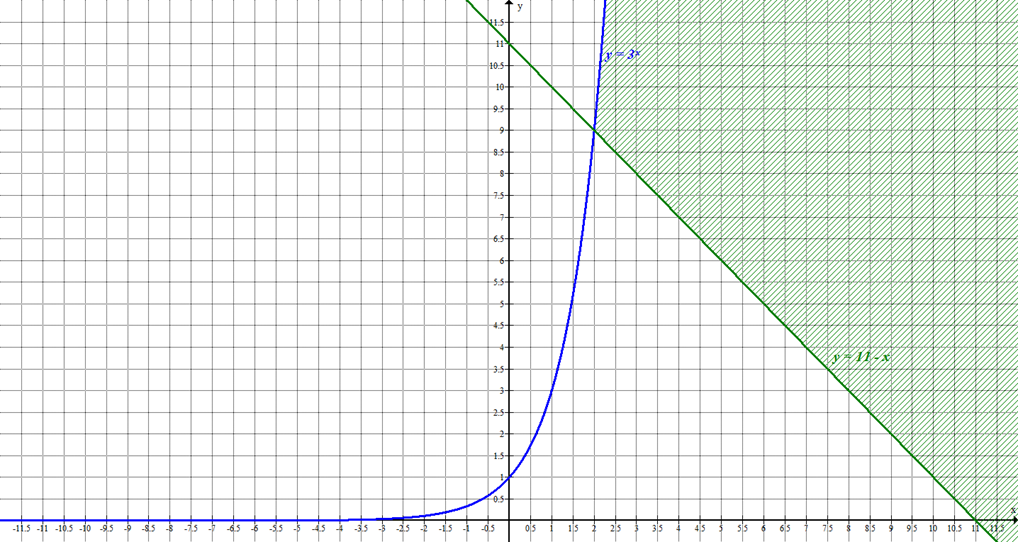
Согласно исходному неравенству, значения показательной функции должны быть больше значений линейной, поэтому, решением неравенства является 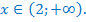
Ответ: 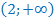 .
.
2). Функциональный метод (с помощью свойств функций)
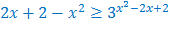
Ветви параболы 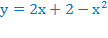 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине:
направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине:
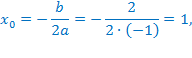
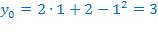
Другими словами, 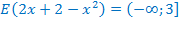
Ветви параболы 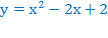 , стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине:
, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине:
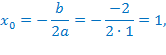
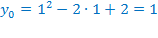
Вместе с этим, ограниченной снизу оказывается и функция 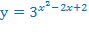 , стоящая в правой части неравенства. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно
, стоящая в правой части неравенства. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 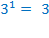 . Значит,
. Значит, 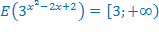 .
.
Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке 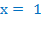 .
.
Ответ: 
5) Метод почленного деления заключается в том, чтобы разделить каждый член неравенства, содержащий степени с одинаковыми показателями, но разными основаниями, на одну из степеней. Это без страха можно сделать, поскольку значение показательной функции строго положительно. Этот метод применяется для решения однородных показательных неравенств.
Например, 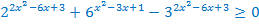
Произведём преобразования, используя свойства степеней.
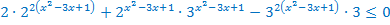
Разделим обе части неравенства на 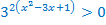 .
.
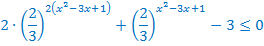
Выполним замену переменной: 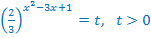
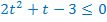
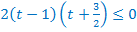
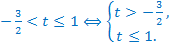
Возвращаемся к исходной переменной:

Первое неравенство системы верно при любых значениях х, значит, осталось решить второе неравенство.
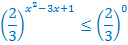
Т.к. 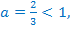 то функция убывающая, поэтому, сравнивая показатели степеней, знак неравенства меняем на противоположный.
то функция убывающая, поэтому, сравнивая показатели степеней, знак неравенства меняем на противоположный.
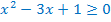
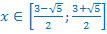 .
.
Ответ: 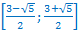 .
.
1) Метод группировки заключается в том, чтобы собрать степени с одинаковыми основаниями в одной части неравенства, а затем разделить обе части уравнения на одну из степеней (всё ещё помним, что делить на степень имеем полное право, поскольку значение показательной функции положительно).
Например, 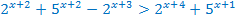
Соберём в левой части степени с основанием 2, а в правой части степени с основанием 5.
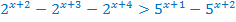
Преобразуем выражение, используя свойства степеней.
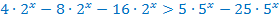
Вынесем за скобки общий множитель в правой и в левой части.
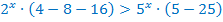

Разделим обе части на 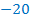 , не забыв, при этом, поменять знак неравенства.
, не забыв, при этом, поменять знак неравенства.

Разделим обе части неравенства на  .
.
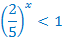
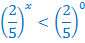
Основание степени меньше единицы, поэтому, сравнивая показатели степеней, меняем знак неравенства на противоположный.

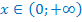
Ответ: 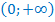
1. Решить неравенства:
1) 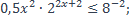
| 2) 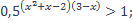
| 3) 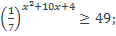
|
4) 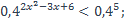
| 5) 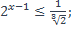
| 6) 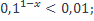
|
7) 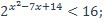
| 8) 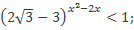
| 9) 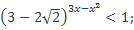
|
10) 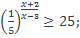
| 11) 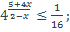
| 12) 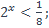
|
13) 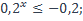
| 14) 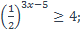
| 15) 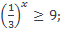
|
16) 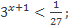
| 17) 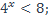
| 18) 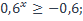
|
19) 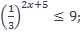
| 20) 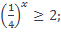
| 21) 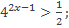
|
22) 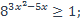
| 23) 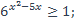
| 24) 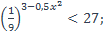
|
25) 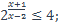
| 26) 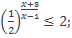
| 27) 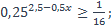
|
28) 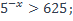
| 29) 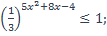
| 30) 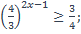
|
31) 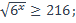
| 32) 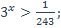
| 33) 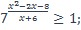
|
34) 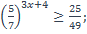
| 35) 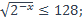
| 36) 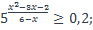
|
37) 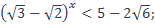
| 38) 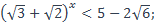
| 39) 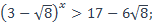
|
40) 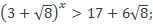
| 41) 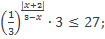
| 42) 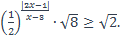
|
2. Найти решения неравенств:
1) 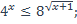
| 2) 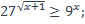
| 3) 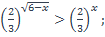
|
4) 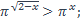
| 5) 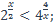
| 6) 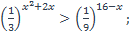
|
7) 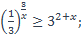
| 8) 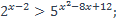
| 9) 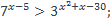
|
10) 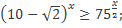
| 11) 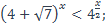
| 12) 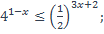
|
13) 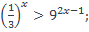
| 14) 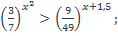
| 15) 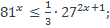
|
16) 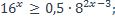
| 17) 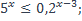
| 18) 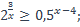
|
19) 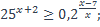
| 20) 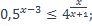
| 21) 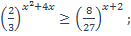
|
22) 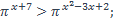
| 23) 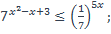
| 24) 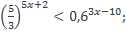
|
25) 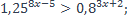
| 26) 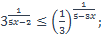
| 27) 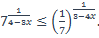
|
3. Решить неравенства:
1) 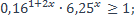
| 2) 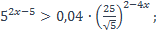
| 3) 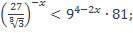
| |
4) 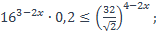
| 5) 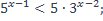
| 6) 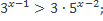
| |
7) 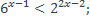
| 8) 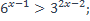
| 9) 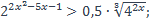
| |
10) 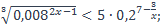
| 11) 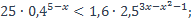
| ||
12) 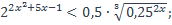
| 13) 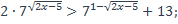
| ||
14) 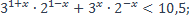
| 15) 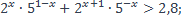
| ||
16) 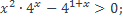
| 17) 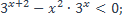
| ||
18) 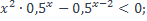
| 19) 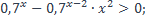
| ||
20) 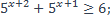
| 21) 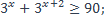
| ||
22) 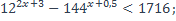
| 23) 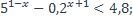
| ||
24) 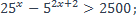
| 25) 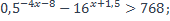
| ||
26) 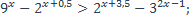
| 27) 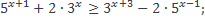
| ||
28) 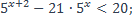
| 29) 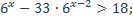
| ||
30) 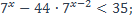
| 31) 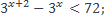
| ||
32) 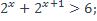
| 33) 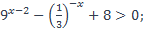
| ||
34) 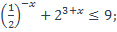
| 35) 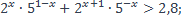
| ||
36) 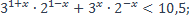
| 37) 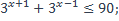
| ||
38) 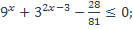
| 39) 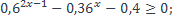
| ||
40) 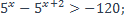
| 41) 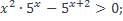
| ||
42) 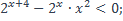
| 43) 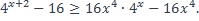
| ||
4. Решить неравенства:
1) 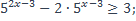
| 2) 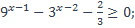
|
3) 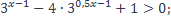
| 4) 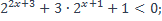
|
5) 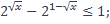
| 6) 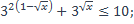
|
7) 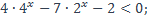
| 8) 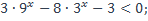
|
9) 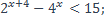
| 10) 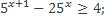
|
11) 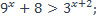
| 12) 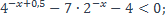
|
13) 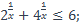
| 14) 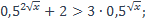
|
15) 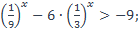
| 16) 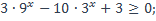
|
17) 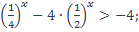
| 18) 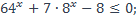
|
19) 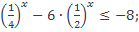
| 20) 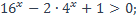
|
21) 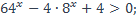
| 22) 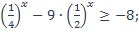
|
23) 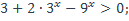
| 24) 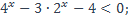
|
25) 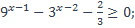
| 26) 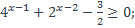
|
27) 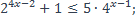
| 28) 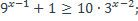
|
29) 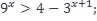
| 30) 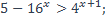
|
31) 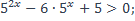
| 32) 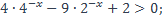
|
33) 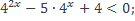
| 34) 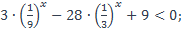
|
5. Найти решения неравенства:
1) 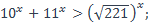
| 2) 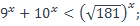
|
3) 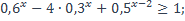
| 4) 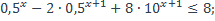
|
5) 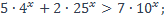
| 6) 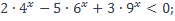
|
7) 
| 8) 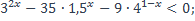
|
9) 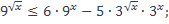
| 10) 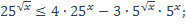
|
11) 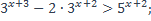
| 12) 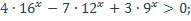
|
13) 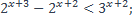
| 14) 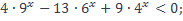
|
15) 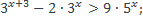
| 16) 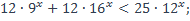
|
17) 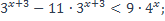
| 18) 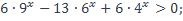
|
19) 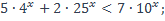
| 20) 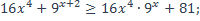
|
21) 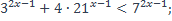
| 22) 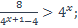
|
23) 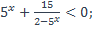
| 24) 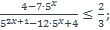
|
25) 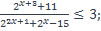
| 26) 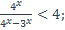
|
27) 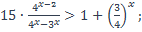
| 28) 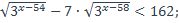
|
29) 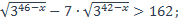
| 30) 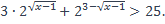
|
6. Решить неравенства:
1) 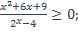
| 2) 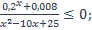
| 3) 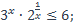
| |
4) 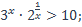
| 5) 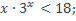
| 6) 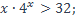
| |
7) 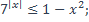
| 8) 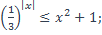
| 9) 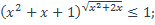
| |
10) 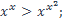
| 11) 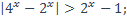
| 12) 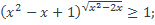
| |
13) 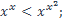
| 14) 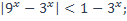
| 15) 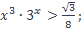
| |
16) 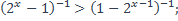
| 17) 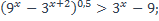
| ||
18) 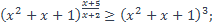
| 19) 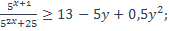
| ||
20) 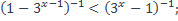
| 21) 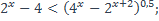
| ||
22) 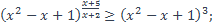
| 23) 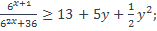
| ||
24) 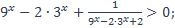
| 25) 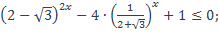
| ||
26) 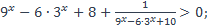
| 27) 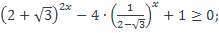
| ||
28) 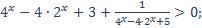
| 29) 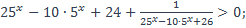
| ||
30) 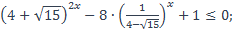
| 31) 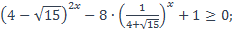
| ||
32) 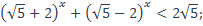
| 33) 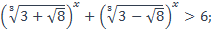
| ||
34) 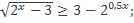
| 35) 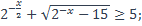
| ||
36) 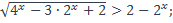
| 37) 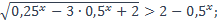
| ||
38) 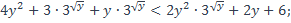
| |||
39) 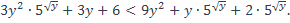
| |||
7. При каких значениях параметра a неравенство выполняется при всех возможных значениях х:
1) 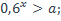
| 2) 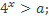
| 3) 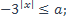
| 4) 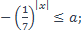
| ||
5) 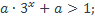
| 6) 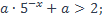
| 7) 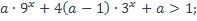
| |||
8) 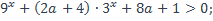
| 9) 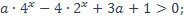
| ||||
8. При каких значениях параметра а неравенство имеет хотя бы одно решение:
1) 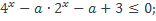
| 2) 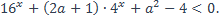
|
9. При каждом значении а решить неравенство:
1) 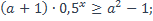
| 2) 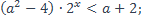
|
3) 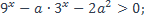
| 4) 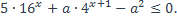
|
10. Решить неравенства. Указать какое-либо отрицательное число, которое является решением неравенства:
1) 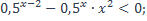
| 2) 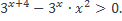
|
11. Найти наименьшее целое число, которое является решением неравенства:
1) 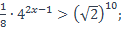
| 2) 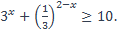
|
12. Найти наибольшее целое число, которое является решением неравенства:
1) 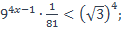
| 2) 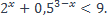
|
13. Решить неравенство 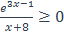 и указать какое-либо целое значение х, не удовлетворяющее данному неравенству.
и указать какое-либо целое значение х, не удовлетворяющее данному неравенству.
14. Найти область определения функции:
1) 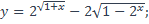
| 2) 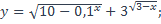
| 3) 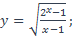
| |
4) 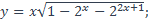
| 5) 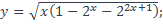
| 6) 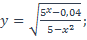
| |
7) 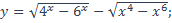
| 8) 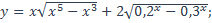
| ||
9) 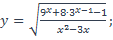
| 10) 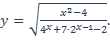
| ||
15. Решить систему:
1) 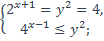
| 2) 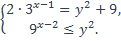
|