Вопросы к экзамену. Экзаменационные билеты

Перечень компетенций с указанием этапов их формирования в процессе освоения образовательной программы

Перечень компетенций с указанием этапов их формирования представлен в п. 3. «Требования к результатам освоения дисциплины» рабочей программы дисциплины.

Описание показателей и критериев оценивания компетенций на различных этапах их формирования, описание шкал оценивания

2.1 Показатели и критерии оценивания компетенций:

ЗУН, составляющие компетенцию	Показатели оценивания	Критерии оценивания	Средства оценивания
Общекультурные компетенции (ОК)
ОК-3: способностью использовать основы экономических знаний в различных сферах деятельности
Знать: методы сбора, анализа и обработки данных, необходимых для решения профессиональных задач; основные законы и методы теории вероятностей и вероятностно-статистического подхода к решению профессиональных задач.	Изучение лекций и учебной литературы; подготовка к практическим занятиям	Полнота и содержательность ответа; умение приводить примеры; умение отстаивать свою позицию; умение пользоваться дополнительной литературой при подготовке к занятиям; соответствие ответов материалам лекции и учебной литературы, сведениям из информационных ресурсов Интернет	О – опрос (О 1-90), С – собеседование (С 1-90), Т – тест (Т 1-40), Р – реферат (Р 1-15)
Уметь: осуществлять выбор, обоснование и применение различных методов теории вероятностей и математической статистики для решения профессиональных задач; использовать методы математической статистики при оценке качества продукции (товаров, работ, услуг) и решении иных профессиональных задач.	Решение разноуровневых задач, в том числе с использованием различных баз данных, современных информационно-коммуникационных технологий и глобальных информационных ресурсов, анализ и интерпретация полученных результатов.	Полнота и содержательность решений; умение отстаивать свою позицию; обоснованность обращения к базам данных; целенаправленность поиска и отбора информации.	Т – тест (Т 1-40), О – опрос (О 1-90), С – собеседование (С 1-90), З – задача (З 1-15)
Владеть: способами и методами решения профессиональных задач с применением системы теоретико-вероятностного и математико-статистического подхода.	Решение разноуровневых задач, в том числе с использованием различных баз данных, современных информационно- коммуникационных технологий и глобальных информационных ресурсов, анализ и интерпретация полученных результатов. Использование ППП для обработки и анализа данных	Полнота и содержательность решений, глубина анализа; умение отстаивать свою позицию; умение пользоваться дополнительной литературой при подготовке к занятиям; соответствие отчета предъявляемым требованиям; степень владения возможностями инструментальных средств.	З – задача (З 1-15)
Профессиональные компетенции (ПК)
ПК-10: владением навыками количественного и качественного анализа информации при принятии управленческих решений, построения экономических, финансовых и организационно-управленческих моделей путем их адаптации к конкретным задачам управления
Знать: основные методы теории вероятностей и математической статистики в их взаимосвязи; основные законы теории вероятностей и вероятностно-статистического подхода к решению профессиональных задач; математико-статистические методы сбора, обработки данных, необходимые для принятия управленческих решений.	Изучение лекций и учебной литературы; подготовка к практическим занятиям	Полнота и содержательность ответа; умение приводить примеры; умение отстаивать свою позицию; умение пользоваться дополнительной литературой при подготовке к занятиям; соответствие ответов материалам лекции и учебной литературы, сведениям из информационных ресурсов Интернет	О – опрос (О 1-90), С – собеседование (С 1-90), Т – тест (Т 1-40), Р – реферат (Р 1-15)
Уметь: применять вероятностно-статистические методы для осуществления количественного анализ информации, строить стандартные вероятностно-статистические модели, анализировать результаты исследования при принятии управленческих решений.	Решение разноуровневых задач, в том числе с использованием различных баз данных, современных информационно-коммуникационных технологий и глобальных информационных ресурсов, анализ и интерпретация полученных результатов.	Полнота и содержательность решений; умение отстаивать свою позицию; обоснованность обращения к базам данных; целенаправленность поиска и отбора информации.	Т – тест (Т 1-40), О – опрос (О 1-90), С – собеседование (С 1-90), З – задача (З 1-15)
Владеть: навыки реализации вероятностно-статистических методов количественного анализа и моделирования при принятии управленческих решений.	Решение разноуровневых задач, в том числе с использованием различных баз данных, современных информационно- коммуникационных технологий и глобальных информационных ресурсов, анализ и интерпретация полученных результатов. Использование ППП для обработки и анализа данных	Полнота и содержательность решений, глубина анализа; умение отстаивать свою позицию; умение пользоваться дополнительной литературой при подготовке к занятиям; соответствие отчета предъявляемым требованиям; степень владения возможностями инструментальных средств.	З – задача (З 1-15)

2.2 Шкалы оценивания:

Текущий контроль успеваемости и промежуточная аттестация осуществляется в рамках накопительной балльно-рейтинговой системы в 100-балльной шкале:

84-100 баллов (оценка «отлично»)

67-83 баллов (оценка «хорошо»)

50-66 баллов (оценка «удовлетворительно»)

0-49 баллов (оценка «неудовлетворительно»)

Типовые контрольные задания или иные материалы, необходимые для оценки знаний, умений, навыков и (или) опыта деятельности, характеризующих этапы формирования компетенций в процессе освоения образовательной программы

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Ростовский государственный экономический университет (РИНХ)»

Кафедра статистики, эконометрики и оценки рисков

Вопросы к экзамену

по дисциплинеТеория вероятностей и математическая статистика

1. Предмет и основные определения теории вероятностей.

2. Классическое определение вероятности. Свойства вероятности, вытекающие из классического определения. Примеры.

3. Статистическое определение вероятности, его особенности и связь с классическим определением.

4. Полная группа несовместных событий, противоположные события, свойства их вероятностей.

5. Зависимые и независимые события. Условные и безусловные вероятности.

6. Теоремы умножения вероятностей.

7. Теоремы сложения вероятностей.

8. Формула полной вероятности. Формулы Байеса.

9. Комбинаторика: размещение, сочетания, перестановки и перестановки с повторениями.

10. Дискретные и непрерывные случайные величины. Закон распределения случайной величины и способы его задания.

11. Формула Бернулли. Биномиальное распределение. Наивероятнейшее число наступления событий.

12. Формула Пуассона. Закон распределения редких событий.

13. Числовые характеристики случайных величин. Начальные и центральные моменты. Асимметрия и эксцесс.

14. Математическое ожидание случайной величины. Его смысл и примеры.

15. Свойства математического ожидания.

16. Дисперсия и среднее квадратическое отклонение случайной величины. Их смысл и примеры вычисления.

17. Свойства дисперсии и среднего квадратического отклонения.

18. Математическое ожидание, дисперсия и среднее квадратическое отклонение частоты и частости.

19. Непрерывные случайные величины. Дифференциальная и интегральная функции их распределения, их смысл и связь между ними.

20. Вероятность попадания случайной величины в заданный интервал. Вероятность того что непрерывная случайная величина примет точное наперед заданное значение.

21. Равномерный закон распределения.

22. Нормальное распределение. Плотность нормального распределения и ее свойства.

23. Нормированное (стандартное) нормальное распределение. Функция Лапласа: график, свойства, таблицы.

24. Функция нормального распределения случайной величины.

25. Вероятность попадания нормально распределенной случайной величины в заданный интервал.

26. Вероятность заданного отклонения нормальной случайной величины от своего математического ожидания. Правило трех сигм.

27. Понятие о центральной предельной теореме Ляпунова.

28. Закон больших чисел. Понятие о теореме Чебышева. Значение теоремы Чебышева.

29. Закон больших чисел. Теорема Бернулли.

30. Вероятность отклонения частости от вероятности, частоты от наивероятнейшего числа.

31. Предмет и основные задачи математической статистики.

32. Генеральная совокупность и выборка. Сущность выборочного метода.

33. Вариационные ряды. Виды вариаций. Величина интервала. Накопленные частоты (частости).

34. Графическое изображение вариационного ряда. Эмпирическая функция распределения.

35. Числовые характеристики вариационного ряда. Средняя арифметическая и ее свойства, мода и медиана. Квантили.

36. Показатели колеблемости: вариационный размах, среднее линейное отклонение, дисперсия, коэффициент вариации. Свойства дисперсии.

37. Моменты (начальные и центральные). Показатели асимметрии и эксцесса.

38. Дисперсия альтернативного признака.

39. Повторная и бесповторная выборка. Ошибки регистрации и репрезентативности, предельная ошибка выборки.

40. Средняя ошибка выборки, для средней и для доли.

41. Необходимая численность выборки.

42. Статистические оценки параметров распределения (сущность теории оценивания): несмещенность, состоятельность, эффективность оценок.

43. Точечная оценка генеральной средней по выборочной средней.

44. Точечная оценка генеральной дисперсии. “Исправленные” выборочная дисперсия и среднее квадратическое отклонение.

45. Интервальные оценки. Точность оценки. Доверительная вероятность.

46. Методы оценивания параметров распределения: метод моментов и метод максимального правдоподобия, свойства полученных этим методом оценок.

47. Доверительные интервалы для оценки математического ожидания нормального распределения при известном среднем квадратическом отклонении.

48. Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном среднем квадратическом отклонении.

49. Оценка вероятности по частости: точечная и интервальная.

50. Законы распределения Стьюдента, Пирсона, Фишера.

51. Статистическая проверка гипотезы. Статистическая гипотеза: нулевая и альтернативная, параметрическая и непараметрическая. Ошибки I и II рода.

52. Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия. Критическая область. Область принятия гипотезы. Критические точки. Отыскание правосторонней, левосторонней, двусторонней критических областей. Понятие мощности критерия.

53. Проверка гипотезы о нормальном распределении. Критерий согласия Пирсона.

54. Проверка гипотезы о числовом значении дисперсии генеральной совокупности. Проверка гипотезы о равенстве двух дисперсий нормально распределенных генеральных совокупностей.

55. Проверка гипотезы о равенстве двух средних нормально распределенных генеральных совокупностей с известными дисперсиями.

56. Проверка гипотезы о числовом значении генеральной средней нормально распределенной генеральной совокупности при известной и неизвестной генеральных дисперсиях.

57. Проверка гипотезы о равенстве двух средних нормально распределенных генеральных совокупностей при неизвестных равных дисперсиях.

58. Проверка гипотезы о числовом значении генеральной доли (о параметре биномиального закона распределения). Проверка гипотезы о равенстве двух долей нормально распределенных генеральных совокупностей.

59. Построение теоретического закона распределения по данному вариационному ряду.

60. Сравнение нескольких средних при помощи однофакторного дисперсионного анализа.

Составитель ________________________ О.А. Кракашова

^{(подпись)}

«____»__________________20 г.

Экзаменационные билеты

по дисциплине Теория вероятностей и математическая статистика

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Ростовский государственный экономический университет (РИНХ)»

Кафедра статистики, эконометрики и оценки рисков

БИЛЕТ № 1

по дисциплинеТеория вероятностей и математическая статистика

1. Размещения - это

А) соединения из n элементов по m в каждом, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которое отличаются друг от друга порядком расположения элементов;

Б) соединения из n элементов по m в каждом, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которое отличаются друг от другу либо самими элементами (хотя бы одним), либо порядком их расположения;

В) соединения из n элементов по m в каждом, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которое отличаются друг от другу по крайне мере одним элементом;

Г) соединения из n элементов, каждое из которых содержит все элементы, и которые отличаются друг от друга лишь порядком расположения элементов.

2. Вероятность извлечения дамы или туза из колоды в 52 карты равна:

А) ;	В) ;
Б) 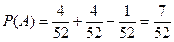;	Г).

3. Статистической вероятностью события А называется:

А) относительная частота (частость) этого события, вычисленная по результатам большого числа испытаний;

Б) частота этого события, вычисленная по результатам испытаний;

В) частота этого события, вычисленная по результатам большого числа испытаний;

Г) относительная частота (частость) этого события, вычисленная по результатам небольшого числа испытаний.

4.Формула полной вероятности может быть записана как:

А)	В)
Б)	Г)

5. Случайные величины бывают

А) дискретными;

Б) непрерывными;

В) условными;

Г) дискретными и непрерывными.

6. Формула Бернулли записывается как:

А)

;

Б)

;

В)

;

Г)

7. Дисперсия СВ, распределенной по гипергеометрическом закону определяется как:

А) ;	В) ;
Б) ;	Г) .

8. Согласно свойствам функции распределения F(x) данная функция:

А) неотрицательная и неубывающая;	В) отрицательная и неубывающая;
Б) положительная и убывающая;	Г) положительная и неубывающая;

9. Интегральная теорема Лапласа записывается как:

А) ;	В) ;
Б) ;	Г) .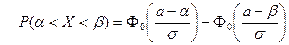

10. Задача: в ходе аудиторской проверки строительной компании аудитор случайным образом отбирает 5 счетов. При условии, что 10% счетов содержат ошибки, Какому закону распределения подчиняется количество счетов с ошибками среди отобранных?

А) биномиальному;	В) равномерному;
Б) гипергеометрическому;	Г) закону распределения Пуассона.

11. Если значение коэффициента асимметрии , то асимметрия:

А) существенная левосторонняя;	В) существенная правосторонняя;
Б) несущественная левосторонняя;	Г) несущественная правосторонняя.

12. Если все варианты ряда уменьшить (увеличить) на постоянную величину k, то дисперсия:

А) не изменится;	В) уменьшится (увеличится) в раз
Б) уменьшится (увеличится) на величину k;	Г) уменьшится (увеличится) в k раз.

13. Коэффициент вариации рассчитывается:

А)

Б)

В)

Г)

14. Доверительный интервал для оценки генеральной средней при собственно-случайной повторной выборке объемом 30 может быть записан как:

А) 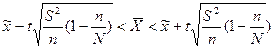;	В) ;
Б) );	Г) ;

15. Теоретической основой выборочного метода является:

А) неравенство Чебышева;	В) лемма Маркова;
Б) теорема Чебышева (частный случай);	Г) теорема Чебышева (общий случай).

16. Сущность выборочного метода состоит в том, что:

А) для изучения вместо всей совокупности элементов берётся лишь некоторая их часть, отобранная по определённым правилам;

Б) для исследования все элементы изучаемой совокупности группируются по определённым правилам;

В) элементы изучаемой совокупности отбираются через определённый интервал;

Г) сначала обследуются все элементы изучаемой совокупности, а затем по определённым правилам отбирается их некоторая часть.

17. Необходимый объем выборки для оценки генеральной средней при собственно- случайном повторном отборе может быть найден как:

А)

;

Б)

;

В)

;

Г)

;

18. При помощи - критерия Пирсона осуществляется проверка гипотезы о

А) числовом значении доли;

Б) равенстве двух генеральных средних с неизвестными дисперсиями;

В) равенстве двух генеральных дисперсий;

Г) нормальном распределении генеральной совокупности.

19. Критические области бывают:

А) только односторонними;	В) только трехсторонними;
Б) только двухсторонними;	Г)одно- или двухсторонними.

20. Задача: в молочном отделе универсама произведено контрольное взвешивание десяти 200-грамовых пачек сливочного масла и установлено, что г. и S=4г. Менеджер отдела выдвигает предположение о недобросовестности поставщика. Прав ли он? Уровень значимости принять равным =0,001. Нулевая и альтернативная гипотезы формулируются как:

А)

;

Б)

;

В)

;

Г)

Задача 1

Монета подбрасывается 5 раз составьте закон распределения вероятностей для числа выпадения герба.

Задача 2

Производитель пальчиковых батареек желает оценить среднюю продолжительность их работы. Случайная выборка 12 батареек показала, что выборочная средняя равна 34,2 часа, а выборочное среднее квадратическое отклонение составило 5,9 часа. Найдите 95%-ный доверительный интервал средней продолжительности работы батареек.

Заведующий кафедрой д.э.н., проф. ________________________ Ниворожкина Л.И.

Экзаменатор к.э.н., доц. _______________________ Кракашова О.А.

«»___________ 201___ г.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Ростовский государственный экономический университет (РИНХ)»

Кафедра статистики, эконометрики и оценки рисков

БИЛЕТ № 2

по дисциплинеТеория вероятностей и математическая статистика

1. Директор компании рассматривает заявления о приеме на работу 5 выпускников университета. В компании имеются три одинаковых вакансии. Сколькими способами директор может заполнить эти вакансии? Для решения задачи нужно использовать:

А) формулу сочетаний;	В) формулу размещений;
Б) формулу перестановок;	Г)формулу перестановок с повторениями.

2. Согласно свойствам вероятности, вытекающим из классического определения, вероятность достоверного события равна:

А) нулю

Б) единице

В) двум

Г) трем

3. Теорема умножения вероятностей двух зависимых событий гласит, что:

А) вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого;

Б) вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на безусловную вероятность другого;

В) вероятность произведения двух зависимых событий А и В равна произведению их вероятностей;

Г) вероятность произведения двух зависимых событий А и В равна частному от деления вероятности одного из них на условную вероятность другого.

4. Формула полной вероятности гласит:

А) если событие А может наступить только вместе с одним из событий Н_1,Н_2,Н_3,….,Н_n, образующих полную группу несовместных событий и называемых гипотезами, то вероятность события А равна сумме произведений вероятностей каждого из событий Н_1,Н_2,Н_3,….,Н_n, на соответствующую условную вероятность события А;

Б) если событие А может наступить только вместе с одним из событий Н_1,Н_2,Н_3,….,Н_n, то вероятность события А равна сумме произведений вероятностей каждого из событий Н_1,Н_2,Н_3,….,Н_n, на соответствующую вероятность события А;

В) если событие А может наступить только вместе с одним из событий Н_1,Н_2,Н_3,….,Н_n, образующих полную группу несовместных событий и называемых гипотезами, то вероятность события А равна сумме вероятностей каждого из событий Н_1,Н_2,Н_3,….,Н_n;

Г) если событие А может наступить только вместе с одним из событий Н_1,Н_2,Н_3,….,Н_n, образующих полную группу несовместных событий и называемых гипотезами, то вероятность события А равна сумме соответствующих условных вероятностей события А.

5. Согласно свойствам математического ожидания дискретной случайной величины, математическое ожидание постоянной величины равно:

А) этой постоянной величине;

Б) нулю;

В)единице;

Г) минус единице.

6. Дисперсия биномиального распределения рассчитывается как:

А)

;

Б)

;

В)

;

Г)

7. Формула распределения вероятностей Пуассона записывается как:

А)

;

Б)

;

В)

;

Г)

8. Математическое ожидание НСВ равно:

А)

;

Б)

;

В)

;

Г)

9. Вероятность заданного отклонения нормально распределенной СВ от ее математического ожидания на величину меньшую Δ равна:

А)	В)
Б)	Г)

10. Задача: для соревнований из группы выбрано 4 девушки и 3 юноши. Требуется составить волейбольную команду из 5 человек.. Какому закону распределения подчиняется количество юношей отобранных в команду?

А) биномиальному;	В) равномерному;
Б) гипергеометрическому;	Г) закону распределения Пуассона.

11. Если значение коэффициента эксцесса , то график ряда распределения:

А)островершинный;	В) скошен вправо;
Б) плосковершинный;	Г) скошен влево.

12. Если все варианты ряда уменьшить в одно и то же число раз k, то дисперсия:

А) не измениться;	В) уменьшиться в раз;
Б)уменьшиться на величину k;	Г) увеличиться в k раз.

13. Формула взвешенной дисперсии записывается как:

А)

Б)

В)

Г)

14. Доверительный интервал для оценки генеральной средней при собственно-случайной повторной выборке объемом n <30 может быть записан как:

А) ;	В) ;
Б) );	Г) ;

15. Собственно - случайная выборка ориентирована на отбор элементов из генеральной совокупности в выборочную посредством:

А) использования таблиц случайных чисел;	В) жребия;
Б) отбора элементов из списков через определенный интервал;	Г) использования таблиц случайных чисел или жребия.

16. Необходимый объем выборки для оценки генеральной средней при собственно- случайном повторном отборе может быть найден как:

А)

;

Б)

;

В)

;

Г)

;

17. Малой считается выборка объем которой составляет:

А) менее 20 единиц;

Б) менее 30 единиц;

В) более 20 единиц;

Г) более 30 единиц;

18. Какая из данных гипотез является непараметрической:

А) гипотеза о числовом значении доли;

Б) гипотеза о равенстве двух генеральных средних;

В) гипотеза о равенстве двух генеральных дисперсий;

Г) гипотеза о нормальном распределении генеральной совокупности.

19.. Если конкурирующая гипотеза имеет вид 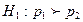, то критическая область:

А) правосторонняя;

Б) левосторонняя;

В) двухсторонняя;

Г) трехсторонняя.

20. Критическая область – это:

А) область допустимых значений критерия;	В) область принятия нулевой гипотезы;
Б) совокупность значений критерия, при которых нулевую гипотезу отвергают;	Г) совокупность значений критерия, при которых нулевую гипотезу нельзя отвергнуть.

Задача 1

На факультете обучается 1000 студентов дневного отделения. По данным прошлых лет известно, что 60 % из них сдает сессии на «хорошо» и «отлично». Какова вероятность того, что 630 студентов сдадут будущую сессию на «хорошо» и «отлично»?

Задача 2

Инженер по контролю качества проверяет среднее время эксплуатации новой модели микроволновой печи. Для проверки случайным образом было отобрано 100 микроволновок, среднее время эксплуатации которых составило 30 месяцев. Среднеквадратическое отклонение для генеральной совокупности известно и равно 20 месяцам. Используя уровень значимости 0,01, проверьте гипотезу о том, что среднее время эксплуатации прибора составит 36 месяцев, которые являются гарантийным сроком работы прибора.

Заведующий кафедрой д.э.н., проф. ________________________ Ниворожкина Л.И.

Экзаменатор к.э.н., доц. _______________________ Кракашова О.А.

«»___________ 201___ г.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Ростовский государственный экономический университет (РИНХ)»

Кафедра статистики, эконометрики и оценки рисков

БИЛЕТ № 3

по дисциплинеТеория вероятностей и математическая статистика

1. Директор компании рассматривает заявления о приеме на работу 5 выпускников университета. В компании имеются три различных вакансии. Сколькими способами директор может заполнить эти вакансии? Для решения задачи нужно использовать:

А) формулу сочетаний;	В) формулу размещений;
Б) формулу перестановок;	Г) формулу перестановок с повторениями.

2. Теорема умножения двух независимых событий гласит, что:

А) вероятность произведения двух независимых событий А и В равна произведению вероятности одного из них на условную вероятность другого;

Б) вероятность произведения двух независимых событий А и В равна произведению вероятности одного из них на безусловную вероятность другого;

В) вероятность произведения двух независимых событий А и В равна произведению их вероятностей;

Г) вероятность произведения двух независимых событий А и В равна частному от деления вероятности одного из них на условную вероятность другого;

3. Совместные события могут быть определены как:

А) несколько событий называются совместными, если в результате опыта наступление одного из них исключает появление других;

Б) несколько событий называются совместными, если в результате опыта наступление одного из них не исключает появление других;

В) несколько событий называются совместными если в результате испытания хотя бы одно из них обязательно произойдет;

Г) несколько событий называются совместными, если в результате испытания.

4. Вероятности гипотез называют:

А) условными;

Б) априорными;

В) апостериорными;

Г)безусловными.

5. Закон распределения дискретно случайной величины может быть задан в виде:

А) только графика распределения;	В) ряда распределения и графика распределения;
Б) только функции распределения;	Г) графика, функции и ряда распределения.

6. Математическое ожидание биномиального распределения рассчитывается как:

А)

;

Б)

;

В)

;

Г)

7. Математическое ожидание СВ, распределенной по гипергеометрическом закону:

А)

;

Б)

;

В)

;

Г)

8. Согласно свойствам функции распределения F(x), вероятность того, что НСВ примет одно определенное значение равна::

А) единице;

Б) нулю;

В) бесконечности;

Г) минус бесконечности.

9. Правило трех сигм формулируется следующим образом:

А) если СВ распределена по нормальному закону, то ее отклонение от математического ожидания не превышает ;

Б) если СВ распределена по нормальному закону, то ее отклонение от математического ожидания не превышает ;

В) если СВ распределена по нормальному закону, то ее отклонение от математического ожидания превышает ;

Г) если СВ распределена по нормальному закону, то ее отклонение от математического ожидания превышает .

10. Задача: для обнаружения некоего минерала было отправлено 6 независимых геологических экспедиций. Вероятность найти требуемый минерал оценивается как 0,05 для каждой экспедиции. Какому закону распределения подчиняется число успешных экспедиций?

А) биномиальному;	В) равномерному;
Б) гипергеометрическому;	Г) закону распределения Пуассона.

11. Если значение коэффициента асимметрии , то асимметрия:

А) существенная левосторонняя;	В) существенная правосторонняя;
Б) несущественная левосторонняя;	Г) несущественная правосторонняя.

12. Медиана интервального вариационного ряда может быть определена по формуле: