Состояния систем, энтропия, расчет энтропии, примеры.

Степень организации элементов в системе связывается с изменением (снижением) энтропии системы по сравнению с суммарной энтропией элементов. Понятие энтропии введено Больцманом для термодинамических систем:

(1.2)

где - вероятность j-го состояния (в теории информации – события); m - возможное число состояний (событий).

Например, два элемента А и В могут каждый принимать два равновероятных состояния: «0»и «1». Вероятность каждого состояния:

Р₁(А) = Р₂(А) = Р₁(В) = Р₂(В) = 0,5.

Для одного элемента энтропия составит

Н(А) = Н(В) = -0,5 log₂0,5 - 0,5log₂0,5 = 1.

Энтропия двух элементов:

Н(А) + Н(В) = 1 + 1 = 2. ¨

Допустим, что система S элементов А и В может принимать три состояния: «-1», «0», «1» с вероятностями Р₁(S) = Р₃(S) = 0,2; Р₂ = 0,6.

Тогда

Н(S) = -2^.0,2^.log₂0,2 - 0,6^.log₂0,6 = -0,4×(-2,32) - 0,6×(-0,737) = 1,37.

Энтропия системы S меньше суммы энтропий элементов А и В на

DН = Н(А) + Н(В) - Н(S) = 2 - 1,37 = 0,63. ¨

Для расчета изменения энтропии системы через вероятности состояний очень часто используется метод Колмогорова.

Допустим, дана структурная схема (граф) состояний подсистемы S (см. рис. 1.2). Исходным состоянием системы с равной степенью вероятности может быть одно из четырех состояний, т.е.

.

Будем считать, что интенсивности переходов l₂₁, l₃₂, l₄₃, l₁₄, l₂₄ заданы. Тогда можно показать, что скорости изменения вероятности нахождения системы в i-м состоянии определяются как , (1.3)

где ; n – число узлов графа (количество состояний);

m_j 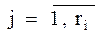- интенсивности переходов по дугам, входящим в i-й узел;

r_i – число дуг, входящих в i-й узел;

l_k 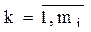- интенсивности переходов по дугам, исходящим из i-го узла;

m_i – число дуг, выходящих из i-го узла;

P_i и P_j – вероятности нахождения системы в i-м и j-м состояниях

соответственно.

Заметим, что

.

Установившееся значение вероятности нахождения системы в i-м состоянии определяется из условия

.

Тогда для системы с n состояниями имеем систему из (n + 1) уравнений с n неизвестными:

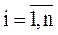; . (1.4)

Одно из уравнений (1.4) можно отбросить, так как оно может быть получено из (n - 1) оставшихся.

Пример. Примем l₂₁ = 0,1, l₃₂ = 0,2, l₄₃ = 0,3, l₁₄ = 0,4, l₂₄ = 0,5. Тогда получаем:

l₁₄^.Р₄ - l₂₁^.Р₁ = 0

l₂₁^.Р₁ + l₂₄^.Р₄ - l₃₂^.Р₂ = 0

l₃₂^.Р₂ - l₄₃^.Р₃ = 0

l₄₃^.Р₃ – (l₁₄ + l₂₄)^.Р₄ = 0

Р₁ + Р₂ + Р₃ + Р₄ = 1.

Из системы отбросим второе уравнение и получим:

- 0,1^.Р₁ + 0^.Р₂ + 0^.Р₃ + 0^.Р₄ = 0

0^.Р₁ + 0,2^.Р₂ – 0,3^.Р₃ + 0^.Р₄ = 0

0^.Р₁ + 0^.Р₂ + 0,3^.Р₃ – 0,9^.Р₄ = 0

1^.Р₁ + 1^.Р₂ + 1^.Р₃ + 1^.Р₄ = 1.

Решение полученной системы: Р₁ = 0,32, Р₂ = 0,36, Р₃ = 0,24, Р₄ = 0,08.

Расчет энтропий ведется по формуле

.

Для исходного состояния

Э₀ = -4 ^. 0,25 ^. log₂0,25 = 2,

для конечного состояния

Э_к = -(0,32 ^. log₂0,32 + 0,36 ^. log₂0,36 + 0,24 ^. log₂0,24 + 0,08 ^. log₂0,08) = 1,835.

То есть, изменение энтропии составляет

DЭ = Э₀ – Э_к = 2 – 1,835 = 0,165. ¨

Существуют два основных подхода к расчету энтропий систем и ценности информации.

Первый подход основан на декомпозиции исходной задачи на этапы вычисления вероятностей апостериорной и априорной вероятности элементарных событий.

Методика расчета включает:

- декомпозицию исходной задачи на последовательность таких элементарных событий, априорная вероятность которых известна, а апостериорная может быть легко рассчитана;

- расчет энтропий (или ценности информации) каждого элементарного события;

- вычисление изменения энтропии исходного состояния по отношению к конечному (или ценности информации) путем суммирования изменений энтропий элементарных этапов (переходов, событий).

Данный подход позволяет избежать вычисление вероятности сложных событий.

Второй подход основывается на использовании условных вероятностей событий. Последние иногда рассчитать довольно сложно.

Таким образом, энтропия выступает в качестве меры хаоса, беспорядка и ее снижение означает увеличение организации.

Для информационных систем степень организации очень часто зависит от количества информации, которая может быть использована для управления.