Динамический синтез рычажного механизма
2.1 Построение плана положений механизма
Выбираю длину звена ОА на чертеже равную 60 мм. Тогда:
(2.1)
где µl – масштабный коэффициент длины, 
;
lOA – длина звена, м;
OA — длина кривошипа на чертеже, мм.
(2.2)
где AВ — длина звена на чертеже, мм.
Аналогичноопределяю длины звеньев AS2, AC, AS4.
Таблица 2.1 Длины звеньев
| Звено | ОА | AB=АS3 | AS2 | AC | CD | S4 |
| Длина звена, м | 0.1219 | 0,29 | 0,17 | 0,32 | 0,25 | 0,125 |
| Длина звена на чертеже, мм |
По полученным данным строю 13 положений механизма.
Крайнее положение точки В будет в случае, когда звенья ОА и АС сойдутся в одну линию. Крайнее верхнее положение точки В на направляющей x-x будет при длине ОС, равной сумме ОА и АС, т.е. равной 218 мм.
2.2 Построение повернутых планов скоростей
Определю угловую скорость кривошипа:
(2.3)
где ω1 – угловая скорость кривошипа, с-1;
n1 – частота вращения коленчатого вала, об/мин.
Линейная скорость точки A:
(2.4)
где vA – скорость точки А, м/с.
Принимаю скорость точки А на чертеже равную 60 мм. Тогда:
(2.5)
где µ v – масштабный коэффициент скоростей,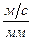 
;
pa — длина вектора скорости на чертеже, мм.
Определяю скорость точки В.
| 2 звено 3 звено | 
| 
| (л.д.  || BA)
(л.д.   x-x)
| (2.6) |
 , т.к. направляющая неподвижна
|
Скорость точки С определяю из соотношения:
Аналогично скорость точки D.
| 4 звено 5 звено | 
| 
| (л.д.  || CD)
(л.д.  y-y)
| (2.7) |
 , т.к. направляющая неподвижна
|
Определение значений линейных и угловых скоростей точек и звеньев механизма
Скорость точки определяется по формуле:
(2.8)
где v т – скорость точки, м/с;
– длина вектора скорости точки на чертеже, мм.
Аналогично определяю скорости остальных точек.
Скорость звена определяется по формуле:
(2.9)
где v зв – скорость звена, м/с;
– длина вектора скорости звена на чертеже, мм.
Аналогично определяю скорости остальных звеньев.
Угловую скорость звена определяю по формуле:
(2.10)
где ωзв – угловая скорость звена, м/с;
lзв – длина звена, мм.
Аналогично определяю угловые скорости звеньев всех положений.
Таблица 2.2 Скорости и угловые скорости точек и звеньев
| № поло-жения | v A,
| v B= v S3,
| v D= v S5
| vc
| v S2,
| v S4,
| v AB ,
| v OA ,
| v AC ,
| v CD ,
| ω2 , c-1 | w4 , c-1 |
|
| |||||||||||
|
| 
|
| 
| 
| 
| 
|
| 
|
| 62,4 | ||
|
|
| 
| 
| 
| 
| 
|
| 
| 
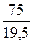
| 21,9 | ||
|
| 
| 
| 
|
| 
| 
|
|
| 
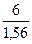
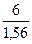
| 4,9 | 63,44 | |
|
| 
| 
| 
|
| 
| 
|
|
|
| 27,6 | 48,88 | |
|
|
| 
| 
| 
| 
| 
|
|
| 
| 43,9 | 29,12 | |
|
| 
| 
|
| 
|
|
|
|
|
| 48,8 | 4,16 | |
|
|
| |||||||||||
|
|
|
| 
|
| 
|
|
| 
| 
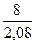
| 42,5 | 18,72 | |
|
|
| 
| 
| 
| 
|
|
| 
| 
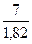
| 22,8 | 43,68 | |
|
| 
|
| 
|
| 
| 
|
| 
| 
| 11,4 | 75,92 | |
|
| 
|
| 
|
|
| 
|
| 
| 
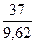
| 33,3 | 84,24 | |
|
| 
|
| 
|
|
|
|
|
| 
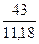
| 47,9 | 67,6 |
Определение приведенной силы сопротивления
Приведенную силу прикладываю на повернутом плане скоростей к концу кривошипа перпендикулярно ему. Силу полезного сопротивления направляю навстречу движению поршня.
Определяю силы тяжести:
(2.11)
где Gзв – сила тяжести звена, Н;
mзв – масса звена, кг;
g=9,8 – ускорение свободного падения, м/с2.
Аналогично для звеньев 3,4,5.
Таблица 2.3 Силы тяжести звеньев
| Звено | ||||
| Сила тяжести звена G, Н | 149,1 | 99,1 | 127,5 | 255,1 |
Определяю масштабный коэффициент графика сил полезного сопротивления:
(2.12)
где µP – масштабный коэффициент силы полезного сопротивления, 
;
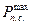– максимальная сила полезного сопротивления, Н;
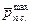– принятое значение 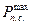на графике, мм.
(2.13)
где Рп.с. – сила полезного сопротивления, кН;
– значение Рп.с. на графике, мм.
Для первого положения точки D:
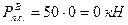
Аналогично определяю силы полезного сопротивления остальных положений механизма.
По графику определяю значения сил полезного сопротивления для каждого поршня.
Таблица 2.3 Значения сил полезного сопротивления
| № поло-жения | |||||||||||||
| |||||||||||||
|
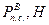
Приведенную силу определяю по методу Жуковского из условия 
.
Таблица 2.4 Формулы для расчета и значения приведенной силы
| № поло-жения | Формула для расчета приведенной силы | Pп, Н |
G2·hG2 + Pп pa=0
Pп=  (-G2·hG2)
Pп =  (-149,1*8)
| -14,91 | |
G2·hG2 + G3·hG3+G4·hG4 -  ·pd + Pп pa=0
Pп= (-G2·hG2 – G3·hG3-G4·hG4+ · pd) Pп = (-149,1*39-99,1*40-127,5*24+150*40)
| -85,48625 | |
G2·hG2 + G3·hG3+G4·hG4- · pd + Pп pa=0
Pп= ( – G2·hG2 – G3·hG3-G4·hG4+ · pd) Pп =  (-149,1*57-99,1*60-127,5*34+2500*34)
| 827,75375 | |
| G2·hG2 + G3·hG3 + G4·hG4- · pd + Pп pa=0
Pп= ( – G2·hG2 – G3·hG3 – G4·hG4+ · pd) Pп = (-149,1*59-99,1*57-127,5*30+2500*11)
| 115,3675 | |
| G2·hG2 + G3·hG3 + G4·hG4 + · pd + Pп pa=0
Pп= ( – G2·hG2 – G3·hG3 – G4·hG4 - · pd) Pп = (-149,1*45-99,1*41-127,5*23-2500*2)
| -233,81375 | |
| G2·hG2 + G3·hG3 + G4·hG4 + · pd + Pп pa=0
Pп= ( – G2·hG2 – G3·hG3 – G4·hG4- · pd) Pп = (-149,1*23-99,1*23-127,5*13-2500*5)
| -248,32625 | |
-G2·hG2 + G4·hG4 + G3·hG3+  · pd +Pп pa=0
Pп=  (G2·hG2 – G4·hG4 – G3·hG3- · pd) Pп = (149,1*2-99,1*3-127,5*2-2500*1)
| -34,42625 |
Продолжение таблицы 2.4
| -G2·hG2 + Pп pa=0
Pп= (G2·hG2) Pп = (149,1*15)
| 27,95625 | |
| -G2·hG2 - G3·hG3 - G4·hG4 - · pd + Pп pa=0
Pп= (G2·hG2 + G3·hG3 + G4·hG4 + · pd) Pп = (149,1*23+99,1*13+127,5*9+2500*4)
| 198,31375 | |
| -G2·hG2 - G3·hG3 - G4·hG4 - · pd + Pп pa=0
Pп= (G2·hG2 + G3·hG3 + G4·hG4+ · pd) Pп = (149,1*45+99,1*38+127,5*21+2500*7)
| 383,16 | |
| -G2·hG2 - G3·hG3 - G4·hG4 +Pп pa=0
Pп= (G2·hG2 + G3·hG3 + G4·hG4) Pп = (149,1*62+99,1*64+127,5*35)
| 250,61375 | |
-G2·hG2 - G3·hG3 - G4·hG4 + Pп pa=0
Pп= (G2·hG2 + G3·hG3 + G4·hG4) Pп =  (149,1*59+99,1*62+127,5*37)
| 245,7325 | |
| -G2·hG2 - G3·hG3 - G4·hG4 + Pп pa=0
Pп= (G2·hG2 + G3·hG3 + G4·hG4) Pп = (149,1*36+99,1*43+127,5*29)
| 166,58 |