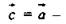1. Проверка домашнего задания:
Дано: А(3; -1; 0), В(0; 0; -7), С(2; 0; 0), D(-4; 0; 4), E(0; -1; 0), F(1; 2; 3), G(0; 5; -7), H(-√5; √3; 0).
Указать: д) точки, лежащие в плоскости Oyz\ е) точки, лежащие в плоскости Oxz.
Решение: д) Точки В(0; 0; -7), Е(0; -1; 0), G(0; 5; -7) - лежат в плоскости Oyz, е) Точки В(0; 0; -7), С(2; 0; 0), D(-4; 0; 3) - лежат в плоскости Oxz.
Дополнительные вопросы:
- Как называются координаты точки в пространстве?
- Дать определение вектора.
- Дать определение компланарных векторов.
б) Второй учащийся выполняет у доски задание по карточке.
Начертить прямоугольную трехмерную систему координат и отметить в ней точки А(1; 4; 3), В(0; 5; -3), С(0; 0; 3) и D(4; 0; 6).
Решение (рис. 2):
Дополнительные вопросы:
- Как расположена точка относительно прямоугольной системы координат, если ее а) абсцисса равна нулю; б) ордината равна нулю; в) аппликата равна нулю; г) абсцисса и ордината равны нулю?
Вопросы:
- Как вводится декартова система координат в пространстве?
- При каких условиях говорят, что задана прямоугольная система координат?
- Объясните, как определяются координаты точки в пространстве?
- Используя рисунок (рис. 3), определить координаты точек А, В, С и D.
- Как располагаются точки относительно системы координат, если а) одна ее координата равна нулю; б) две ее координаты равны нулю?
Примеры:
- Объясните, почему все точки, лежащие на прямой, параллельной плоскости Оху, имеют одну и ту же аппликату?
- Даны точки А(2; 4; 5), В(3; а; b), С(0; 4; d) и D(5; n; m). При каких значениях а, в, d, n и m эти точки лежат:
а) в плоскости, параллельной плоскости Оху;
б) в плоскости, параллельной плоскости Oxz;
в) на прямой параллельной оси 0x1
Ответ: а) а, n - любые; b = d = 5, б) а = n = 4; b, d, m — любые, в) а = n = 4; b = d = m = 5.
|
|
Ход урока:
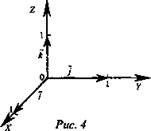
1. Построим прямоугольную систему координат Оху, откладывают от начала координат на осях ох, оу и oz единичные векторы соответственно 
Их называют координатными векторами (рис. 4).
2. Так как векторы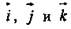 
некомпланарны, то любой вектор пространства 
можно разложить в виде 
где х, у и z определяются единственным образом и являются координатами вектора . Обозначается 
Пример: Рассмотрев рисунок 5, где ОА1 = 2, ОА2 = 3, ОА = 3, определите координаты векторов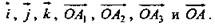 
Решение: 
Все координаты нулевого вектора равны нулю. Обозначается 
Его можно представить в виде: 
3. Вводится правило действий над векторами с заданными координатами и доказываются вместе с учителем. (Можно одно правило доказать с учителем, а остальные, группы учащихся доказывают самостоятельно, затем представители группы доказывают у доски. Можно доказательство задать на дом и проверить на следующем уроке.)
1) Равные векторы имеют равные координаты.
Дано: 
Доказать: x1 = х2, y1 = у2; z1 = z2.
Доказательство: Так как 
то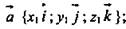 
так как 
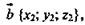то b 
По условию 
Тогда 
Откуда x1 - х2 = 0 и х1 = x2; y1 – y2= 0 и y1 = y2, z1 - z2 = 0 и z1 = z2.
2) Каждая координата суммы двух (и более) векторов равна сумме соответствующих координат этих векторов.
Дано: 
Доказать: 
Доказательство: Так как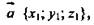 
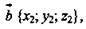то 
то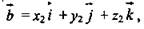 
тогда 
откуда 
3) Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число.
Дано: 
а - произвольное число; 
Доказать: 
Доказательство: Так как 
то 
Значит, 
4) Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
|
|
Дано: 
Доказать: 
Доказательство: 
тогда - 
Тогда 
