Задание 1 – Вычертить изображения контуров деталей и нанести размеры, работа выполняется на А3.








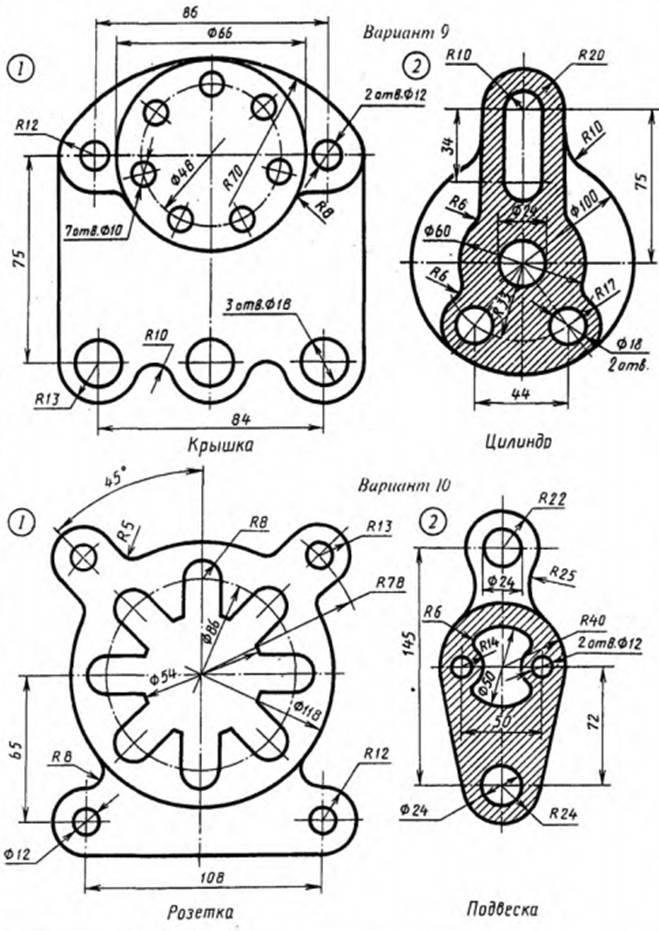






Задание 2 – Выполнить комплексный чертеж каждой модели. Построить по размерам три проекции на формате А4 и аксонометрию (на выбор одну по размерам) выполняется на формате А3.

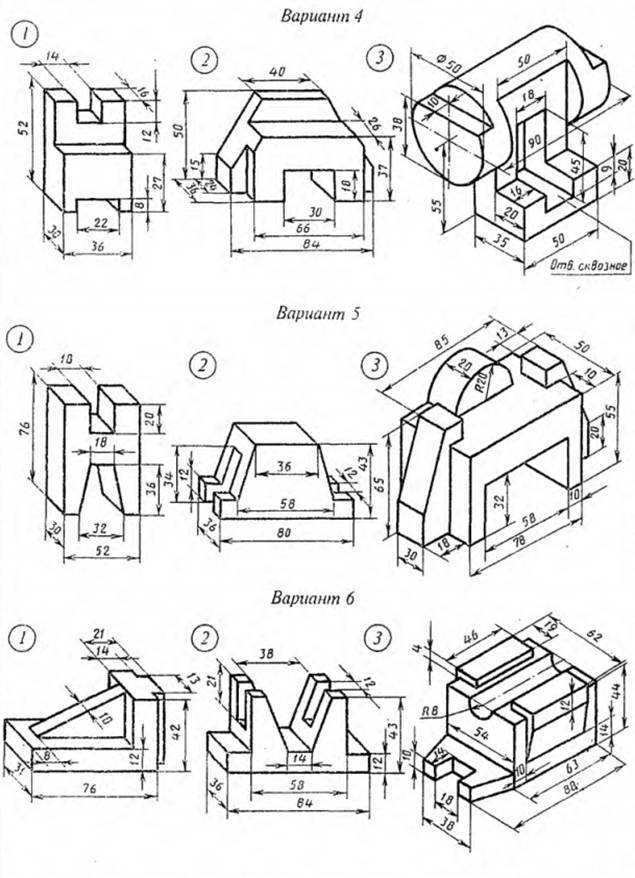





Задание 3 – Простроить третью проекцию по двум заданным с применением простых разрезов, указанных в схеме, выполнять на формате А3.
Образец:











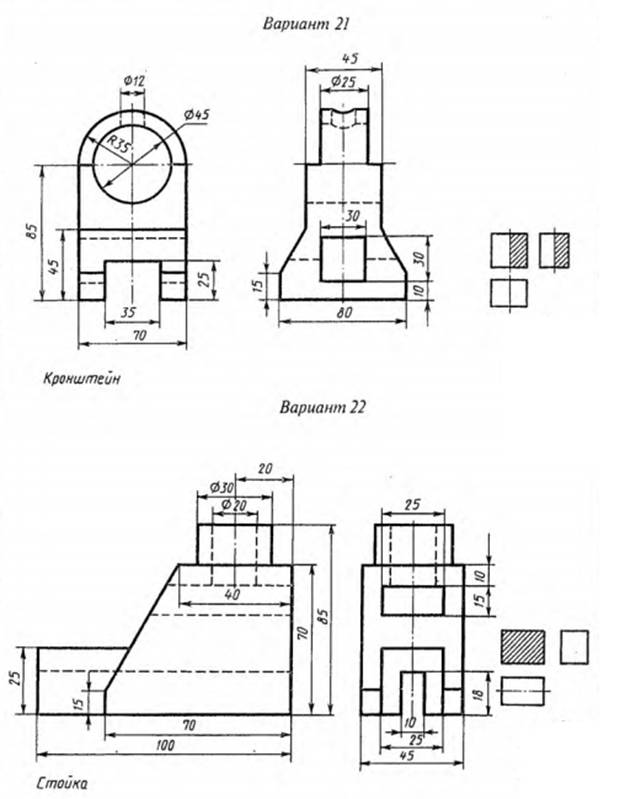
Задание 4 Комплексный чертеж в трех проекциях и аксонометрическую проекцию двух пересекающихся тел.
Образец выполнения приведен на рисунке

Рисунок Образец листа
На листе выполняют: комплексный чертеж в трех проекциях и аксонометрическую проекцию двух пересекающихся тел. Вид аксонометрической проекции выбирается по усмотрению студента. Варианты задания приведены в таблице 1 и чертежи с номером варианта.
Работа выполняется на формате АЗ, масштаб 1:1
Таблица 1 (5)
| № варианта | № чертежа | d или Ь, мм |


|
| 
|
| Чертеж 1 | Чертеж 2 | Чертеж 3 | ||||||||||

|
| 
| ||||||||||
| Чертеж 4 | Чертеж 5 | Чертеж 6 |

Задача 5 На листе формата A3 начертить в трех проекциях чертеж, аксонометрическую (диметрическую) проекцию и развертку граненого тела (призмы или пирамиды), усеченной проецирующей плоскостью.
Указания к решению задачи:
- Данные к решению задачи взять в таблицах 1 и 2.
- Строить чертеж рекомендуется в системе координат.
- Размеры на чертеж не наносить.
- Отсеченные части тел следует изображать тонкими сплошными линиями.
- Показать все три проекции сечения тела плоскостью.
- Действительную величину фигуры сечения следует находить способом замены плоскостей проекций или способом совмещения. Для усвоения обоих способов преобразования чертежа рекомендуется применить на первом чертеже один способ, а на втором — другой.
- Линии штриховки в сечениях следует проводить под утлом 45° к контурной или осевой линии, принятой за основную на данном изображении. Если линии в штриховках совпадают по направлению с линиями контура или осевыми, то вместо угла 45° допускаются углы 30° или 60°.
При построении аксонометрических проекций тел можно применять как «правую», так и «левую» системы координат. Выбор системы определяется положением плоскости среза; при срезе с правой стороны следует применять «левую» систему, при срезе с левой стороны— «правую» систему.
Вид аксонометрической проекции для граненых тел (призма, пирамида) — прямоугольная диметрия.
Плоскость основания и плоскость фигуры сечения на развертке рекомендуется присоединять к одной и той же грани призмы (пирамиды). Линии сгиба в соответствии с ГОСТом 2.303-68* следует изображать штрихпунктирными линиями с двумя точками.
Таблица 2 - Исходные данные к задаче № 5 для построения призмы, мм
| № варианта | обозначение | |||
| d | h | a | α0 | |
Таблица 3- Исходные данные к задаче № 5 для построения призмы, мм
| № варианта | обозначение | |||
| d | h | a | α0 | |

ПРИЛОЖЕНИЕ
Призма Под призмами понимают многогранники, основания которых представляют собой равные многоугольники, а боковые грани — параллелограммы. Если ребра призмы перпендикулярны к плоскости основания, то призму называют прямой. Прямую призму с основанием в виде правильного многоугольника называют правильной.
Фигура сечения прямой пятиугольной призмы фронтально-проецирующей плоскостью f’’0α (рисунок 38) представляет собой плоский пятиугольник 12345.
Для построения проекций фигуры сечения находят проекции точек пересечения плоскости f’’0α с ребрами призмы и соединяют их прямыми линиями. Фронтальные проекции этих точек получаются при пересечении фронтальных проекций ребер призмы с фронтальным следом f’’0α секущей плоскости a’’ (точки 1’’—5’’).
Горизонтальные проекции точек пересечения 1’—5' совпадают с горизонтальными проекциями ребер. Имея две проекции этих точек, с помощью линий связи находят профильные проекции 1’’’—5’’’. Полученные точки 5’’’ соединяют прямыми линиями и получают профильную проекцию фигуры сечения.
Действительный вид фигуры сечения можно определить любым из способов: вращения или перемены плоскостей проекций.
В данном примере (рисунок 38) применен способ перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой 𝜋4, причем ось 𝝅2/𝜋4 (для упрощения построений) совпадает с фронтальным следом плоскости f’’0α.

Рисунок 38
Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).
Развертку боковой поверхности (рисунок 39) с основанием и фигурой сечения призмы строят следующим образом. Проводят прямую, на которой откладывают пять отрезков, равных длинам сторон пятиугольника, лежащего в основании призмы. Из полученных точек проводят перпендикуляры, на которых откладывают действительные длины ребер усеченной призмы, беря их с фронтальной или профильной проекции, получают развертку боковой поверхности призмы.
К развертке боковой поверхности пристраивают фигуру нижнего основания — пятиугольник и фигуру сечения.

Рисунок 39

