25.10.2021
( Написать конспект, заполнить таблицу-канву, и выполнить домашнее задание)
Тема занятия Решение задач «Уравнение сферы, плоскости и прямой. Векторное уравнение прямой и плоскости».
Время 2 урока
ХОД занятия
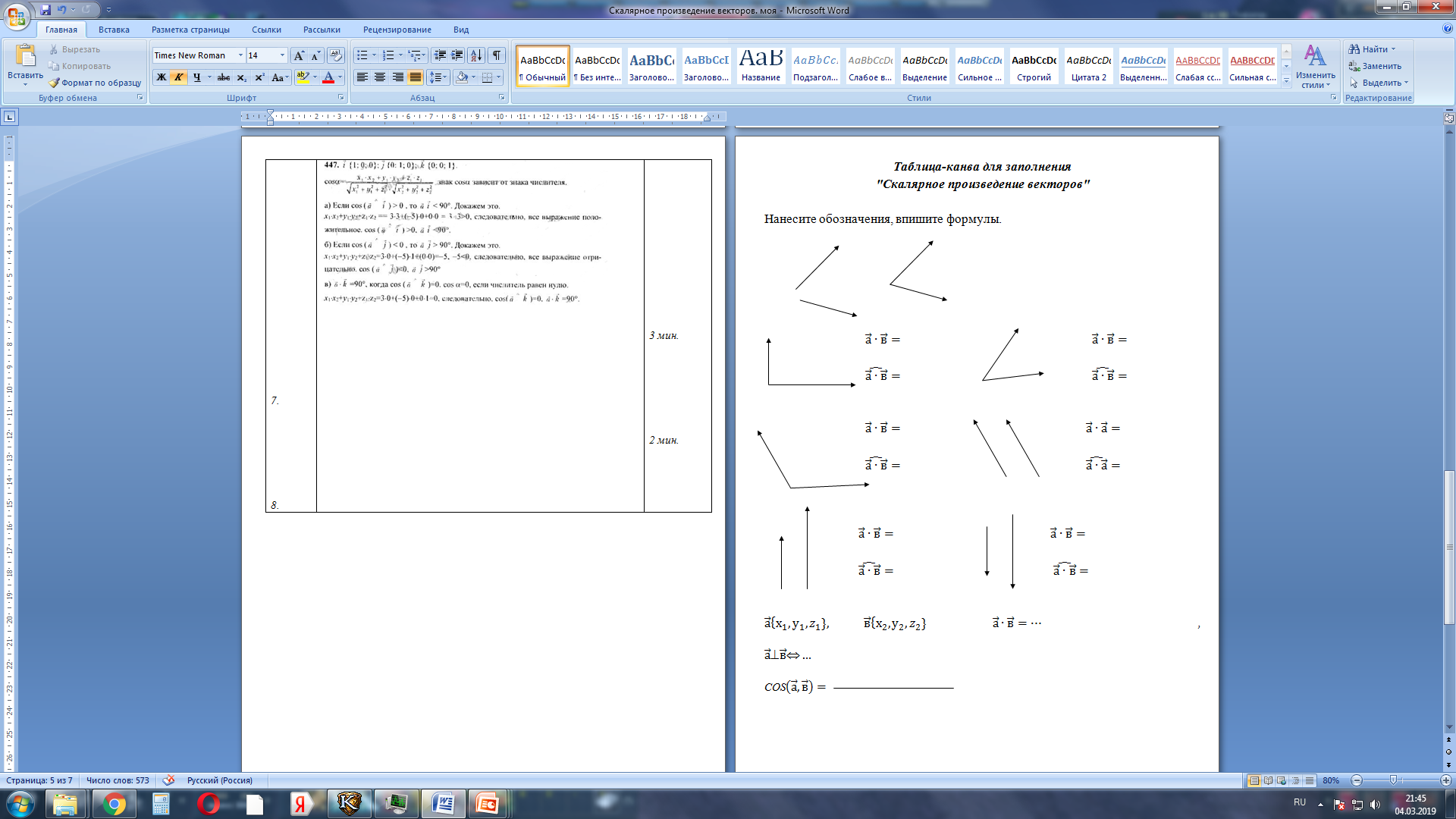 1. Заполнить таблицу-канву (предлагается нанести обозначения, вписать формулы на заготовленную таблицу канву по темам прошлого урока)
1. Заполнить таблицу-канву (предлагается нанести обозначения, вписать формулы на заготовленную таблицу канву по темам прошлого урока)
Изучение нового материала.
1. Уравнение прямой.
Общее уравнение прямой имеет вид ax+by+c=0.
Прямая, параллельная оси Оу, задается уравнением вида х = с. Аналогично, прямая, параллельная оси Ох, задается уравнением вида у = с.
Прямую, не параллельную оси Оу, можно задать уравнением с угловым коэффициентом k: y=kx+b.
Если известны две точки пространства 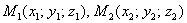 , то уравнения прямой, проходящей через данные 2 точки, выражаются формулами:
, то уравнения прямой, проходящей через данные 2 точки, выражаются формулами:
Если известна некоторая точка пространства 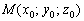 , принадлежащая прямой, и направляющий вектор , принадлежащая прямой, и направляющий вектор 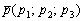 данной прямой, то канонические уравнения этой прямой выражаются формулами: данной прямой, то канонические уравнения этой прямой выражаются формулами:
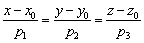 Задача №1. Составить канонические уравнения прямой по точке
Задача №1. Составить канонические уравнения прямой по точке 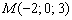 и направляющему вектору и направляющему вектору 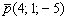
|
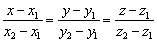
Решение: Канонические уравнения прямой составим по формуле:
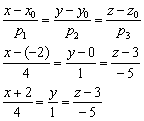
Ответ: 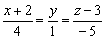
Задача №2. Составить канонические уравнения прямой проходящей по двум точкам: 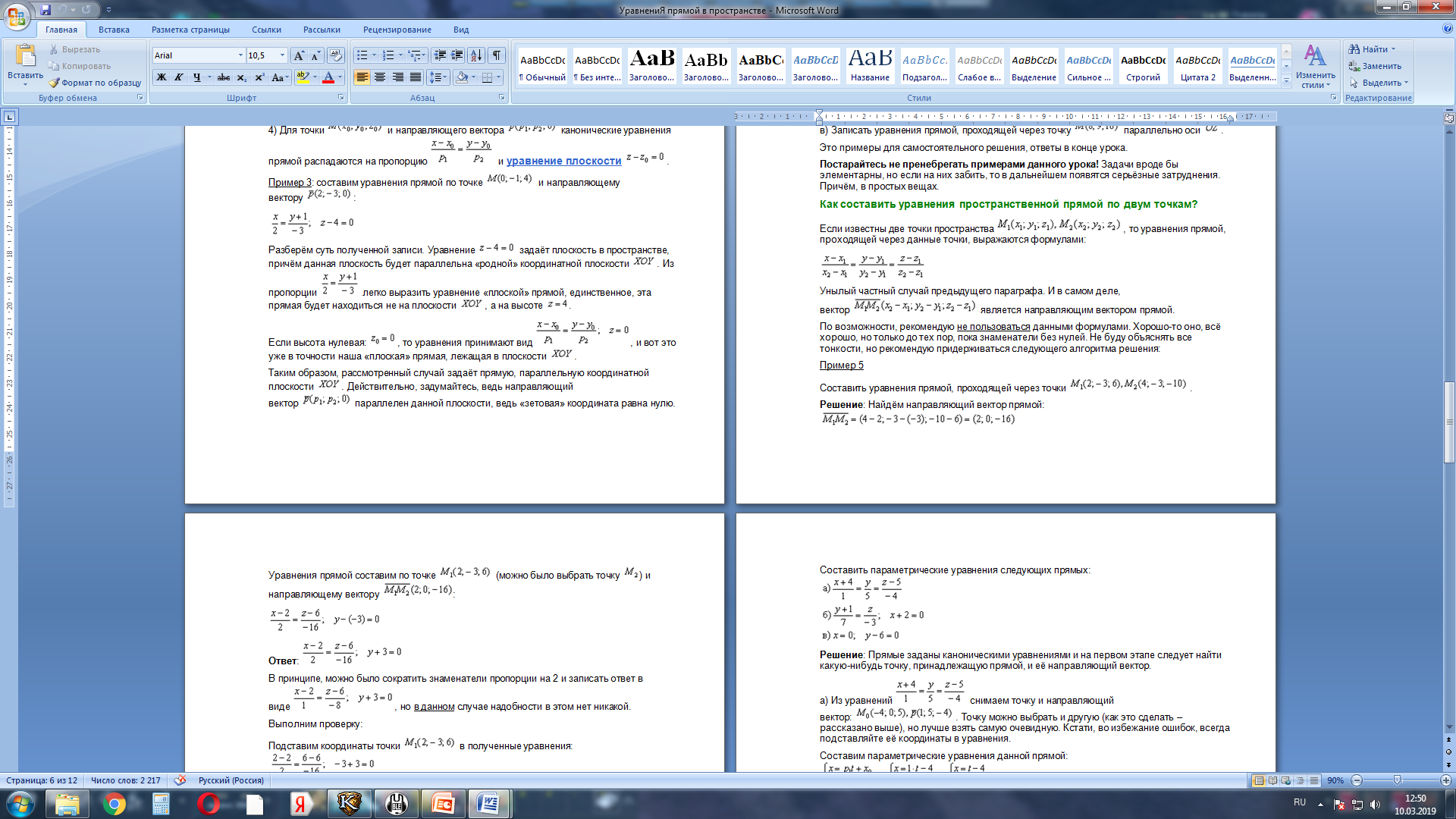
Решение: Канонические уравнения прямой составим по формуле:
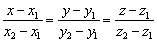
Подставим в уравнение координаты точек М1 и М2:
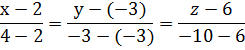
Получим:
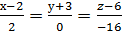 ;
; 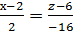 , у+3=0.
, у+3=0.
Выполним проверку:
Подставим координаты точки 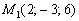 в полученные уравнения:
в полученные уравнения:
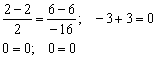
Получены верные равенства.
Подставим координаты точки 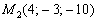 :
:
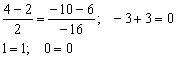
Получены верные равенства.
Уравнение прямой проходящей через 1 данную точку с нормальным вектором:
Определение: Нормальный вектор 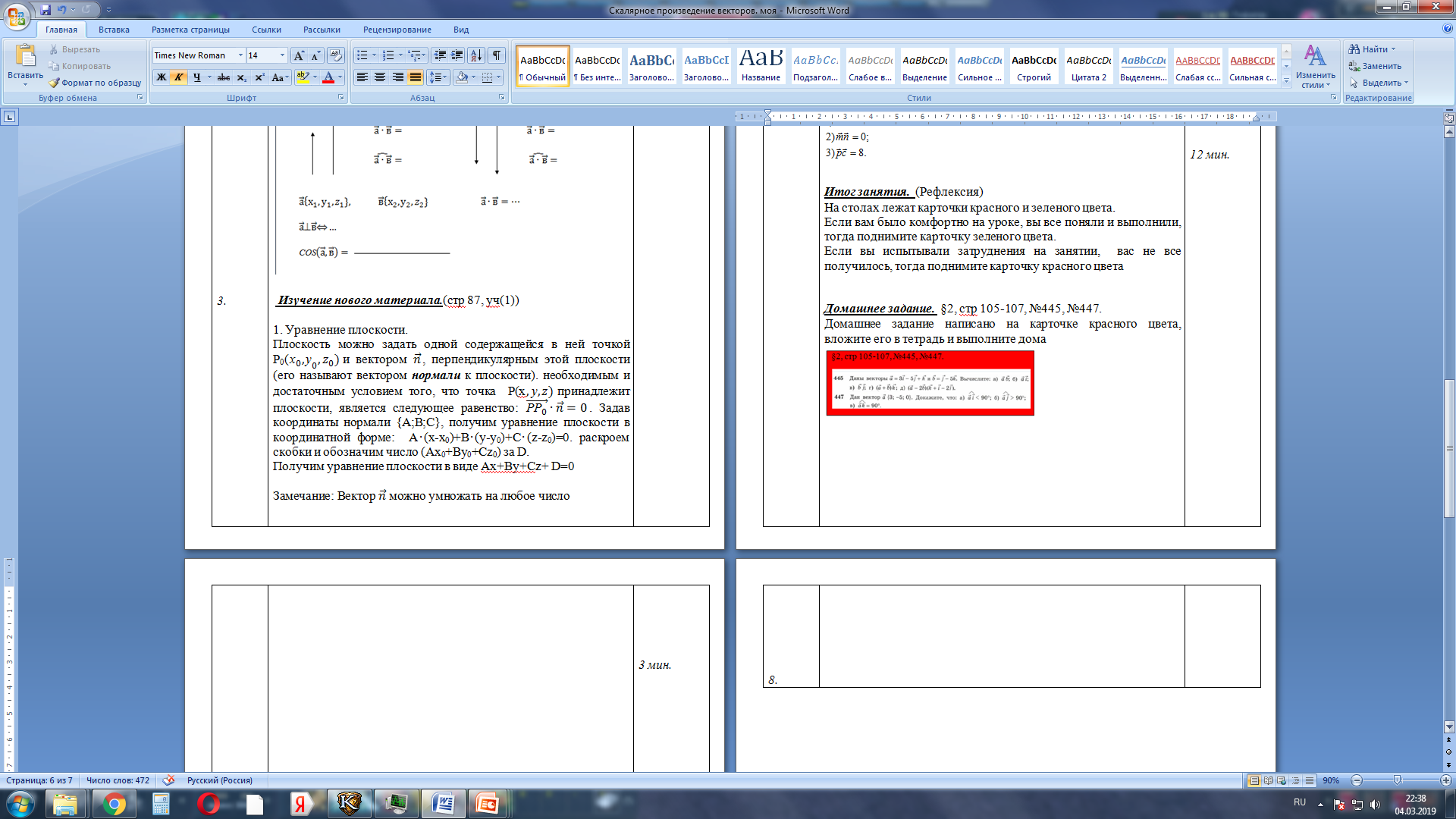 – вектор, перпендикулярный прямой.
– вектор, перпендикулярный прямой.

На плоскости дана точка М0(х0, у0, z0) и вектор 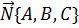 .
.
Составить уравнение прямой на плоскости, проходящей через точку М0 перпендикулярно вектору.
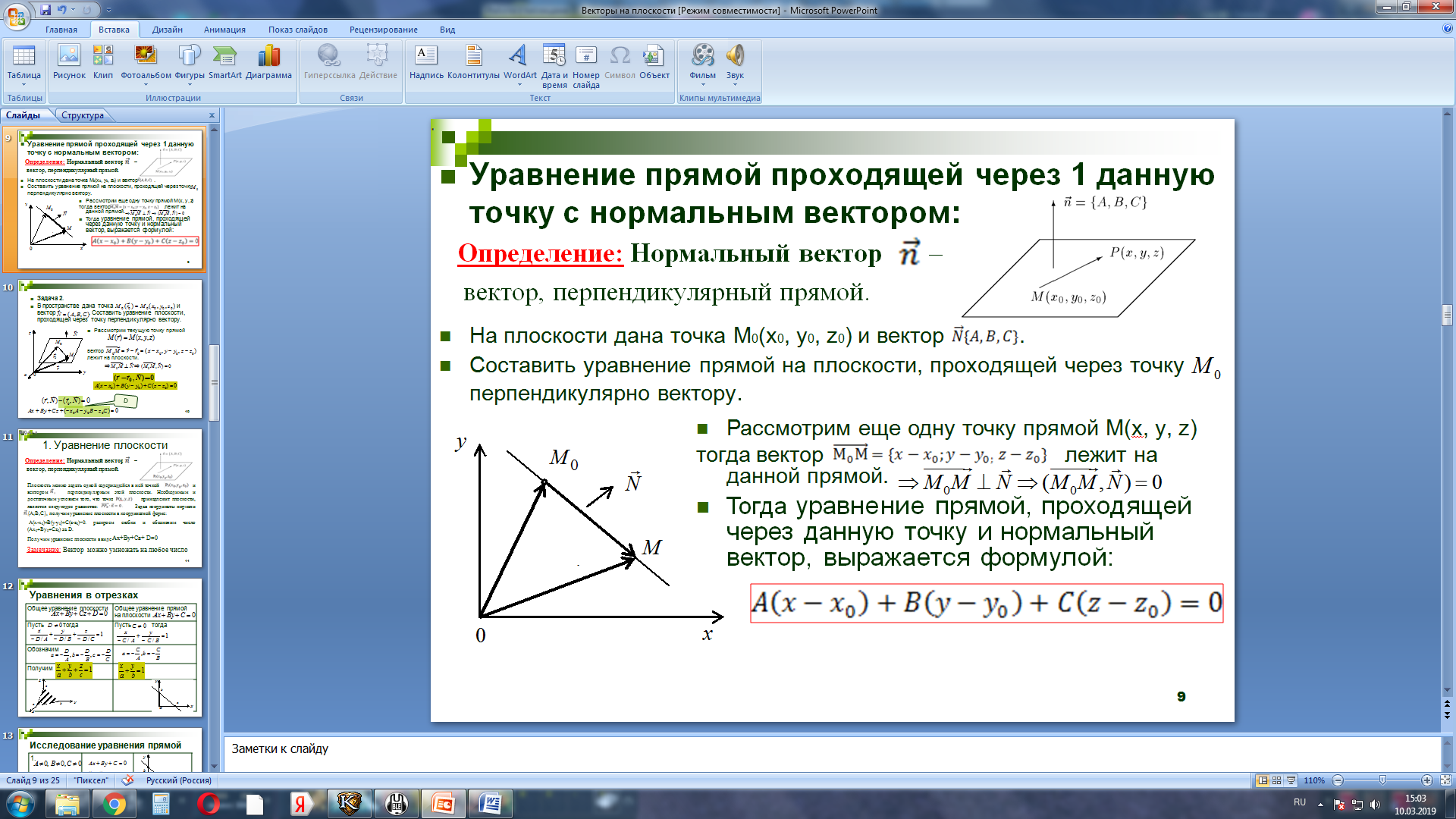 Рассмотрим еще одну точку прямой
Рассмотрим еще одну точку прямой
М(х, у, z), тогда вектор

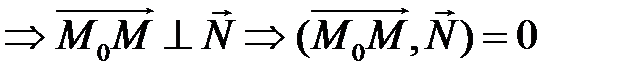 лежит на данной прямой.
лежит на данной прямой.
Тогда уравнение прямой, проходящей через данную точку и нормальный вектор, выражается формулой:
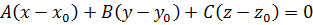
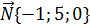 Задача №3. В пространстве дана точка М0(2;-3;0) и вектор. Составить уравнение плоскости, проходящей через точку перпендикулярно вектору
Задача №3. В пространстве дана точка М0(2;-3;0) и вектор. Составить уравнение плоскости, проходящей через точку перпендикулярно вектору
Решение: Канонические уравнения прямой составим по формуле:
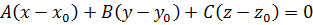
Получим:
-1(х-2)+5(у+3)+0(z-0)=0
-x+2+5y+15=0
5y-x=-15
2. Уравнение плоскости.
Плоскость можно задать одной содержащейся в ней точкой Р0(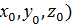 и вектором
и вектором 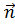 , перпендикулярным этой плоскости (его называют вектором нормали к плоскости). Необходимым и достаточным условием того, что точка Р(х
, перпендикулярным этой плоскости (его называют вектором нормали к плоскости). Необходимым и достаточным условием того, что точка Р(х 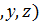 принадлежит плоскости, является следующее равенство:
принадлежит плоскости, является следующее равенство: 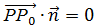 . Задав координаты нормали
. Задав координаты нормали 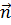 {А;В;С}, получим уравнение плоскости в координатной форме: А
{А;В;С}, получим уравнение плоскости в координатной форме: А  (х-х0)+В
(х-х0)+В  (у-у0)+С
(у-у0)+С  (z-z0)=0. раскроем скобки и обозначим число (Ах0+Ву0+Сz0) за D.
(z-z0)=0. раскроем скобки и обозначим число (Ах0+Ву0+Сz0) за D.
Получим уравнение плоскости в виде Ах+Ву+Сz+ D=0
Замечание: Вектор 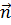 можно умножать на любое число
можно умножать на любое число
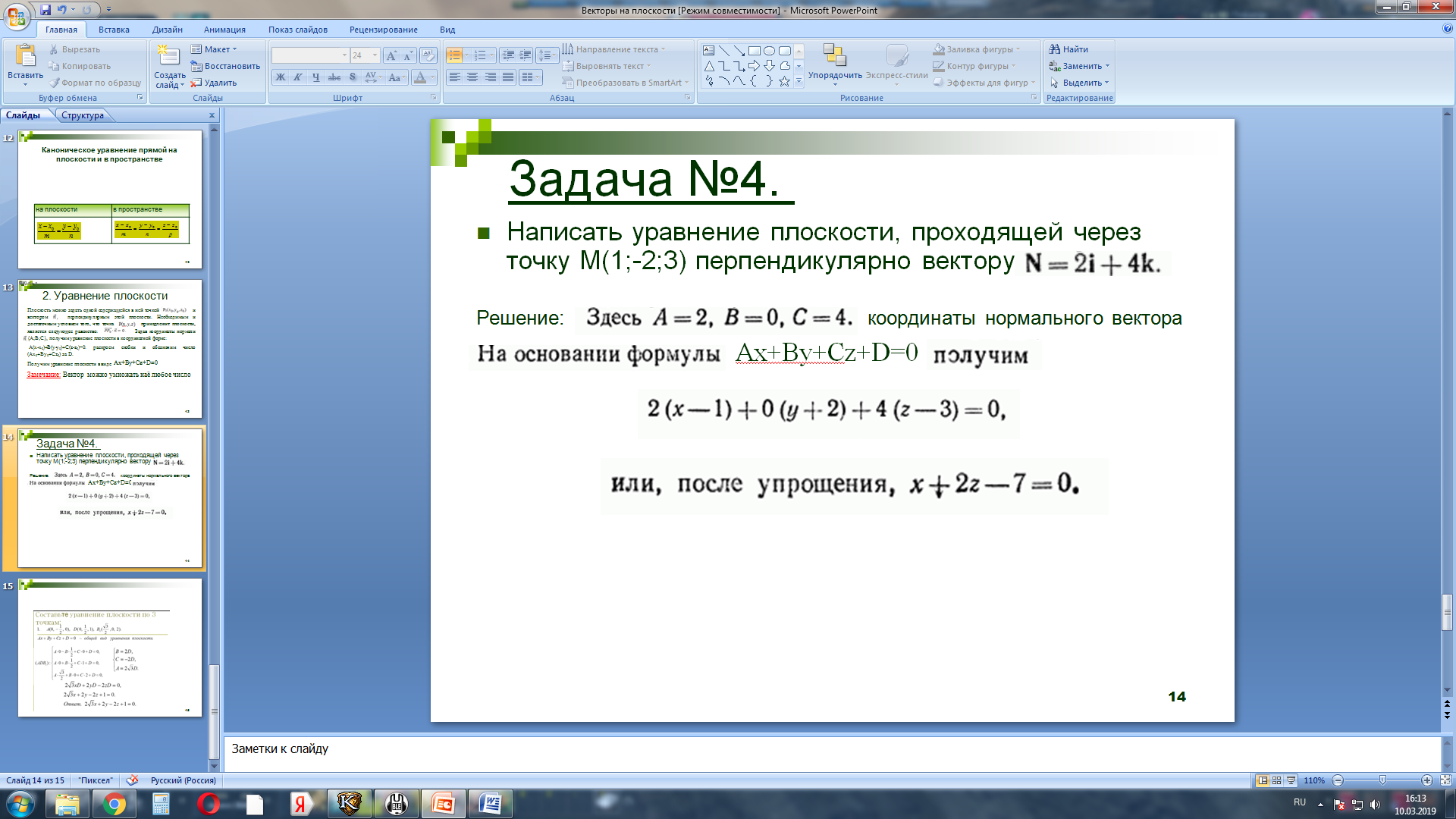
Задача №4. Написать уравнение плоскости, проходящей через точку М(1;-2;3) перпендикулярно вектору 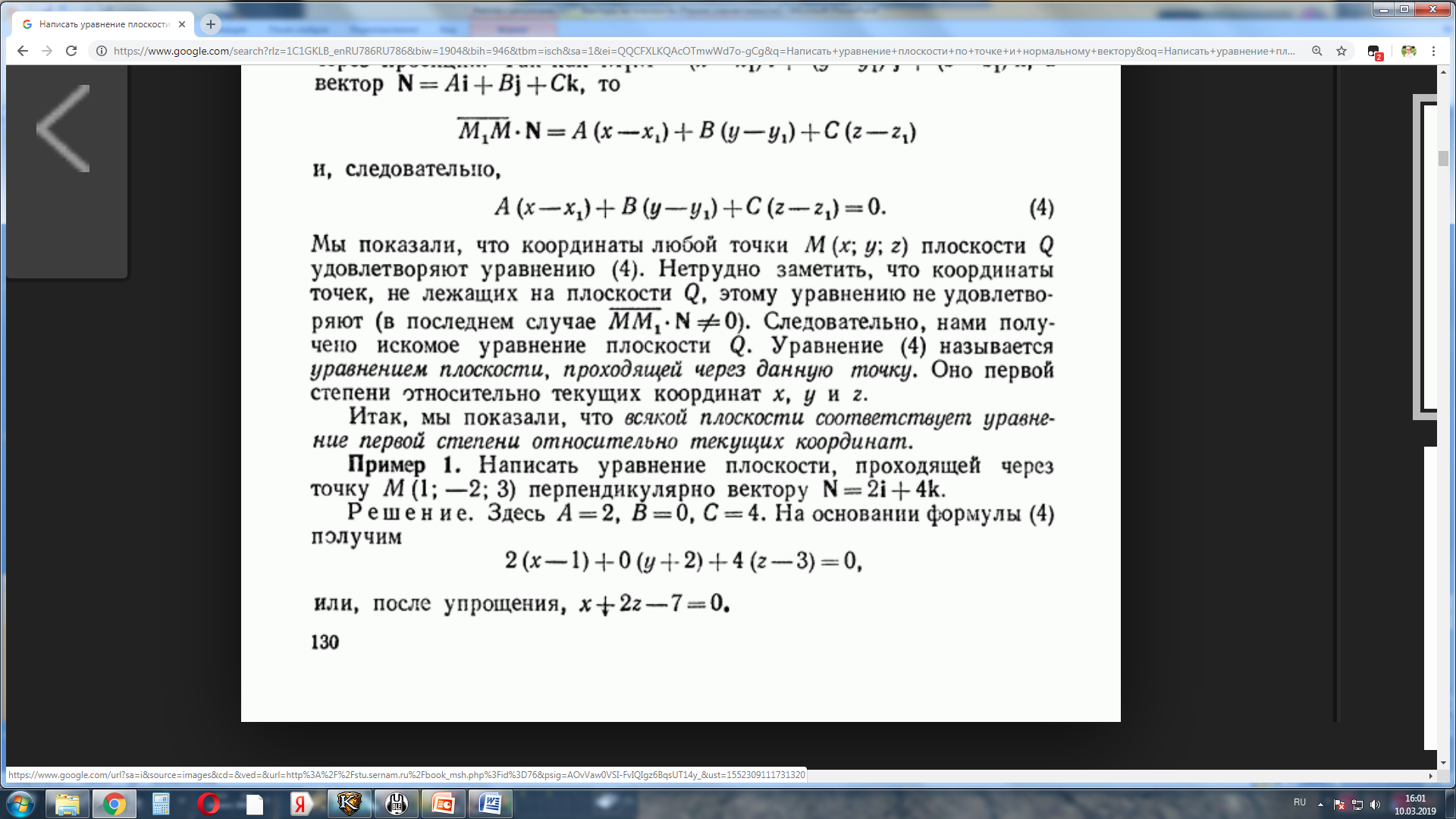
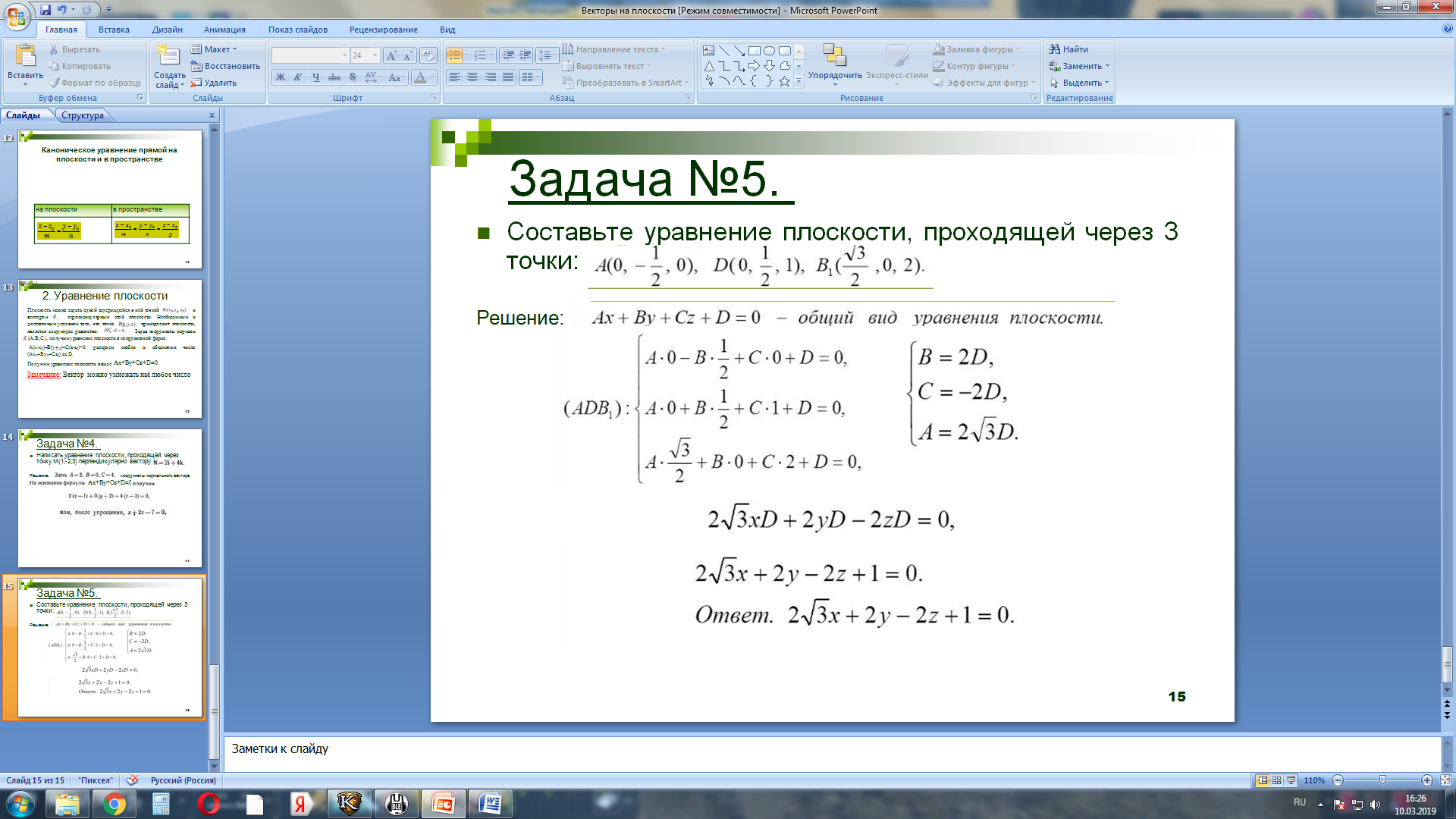
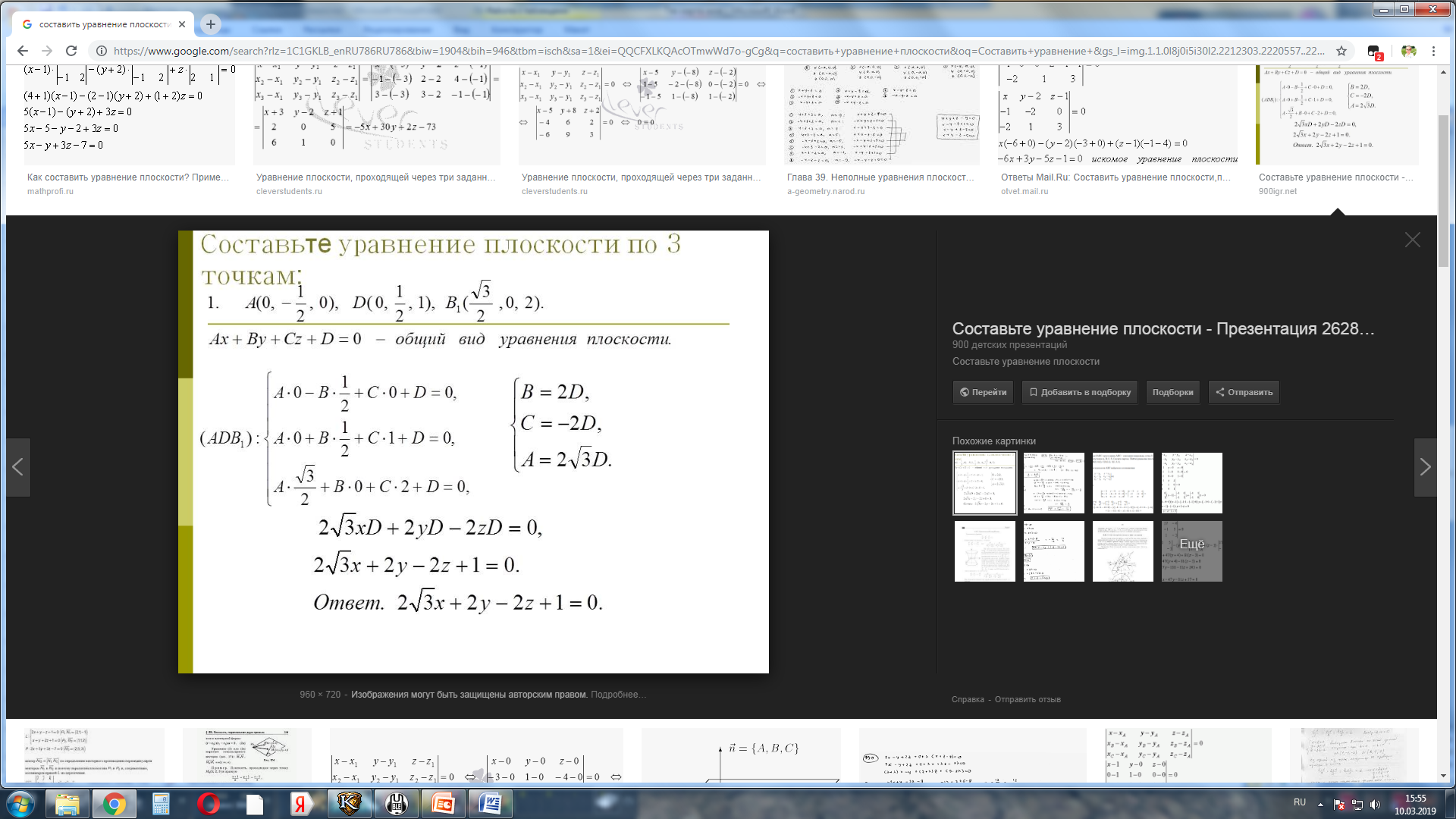 Задача №5. Составьте уравнение плоскости, проходящей через 3 точки:
Задача №5. Составьте уравнение плоскости, проходящей через 3 точки:
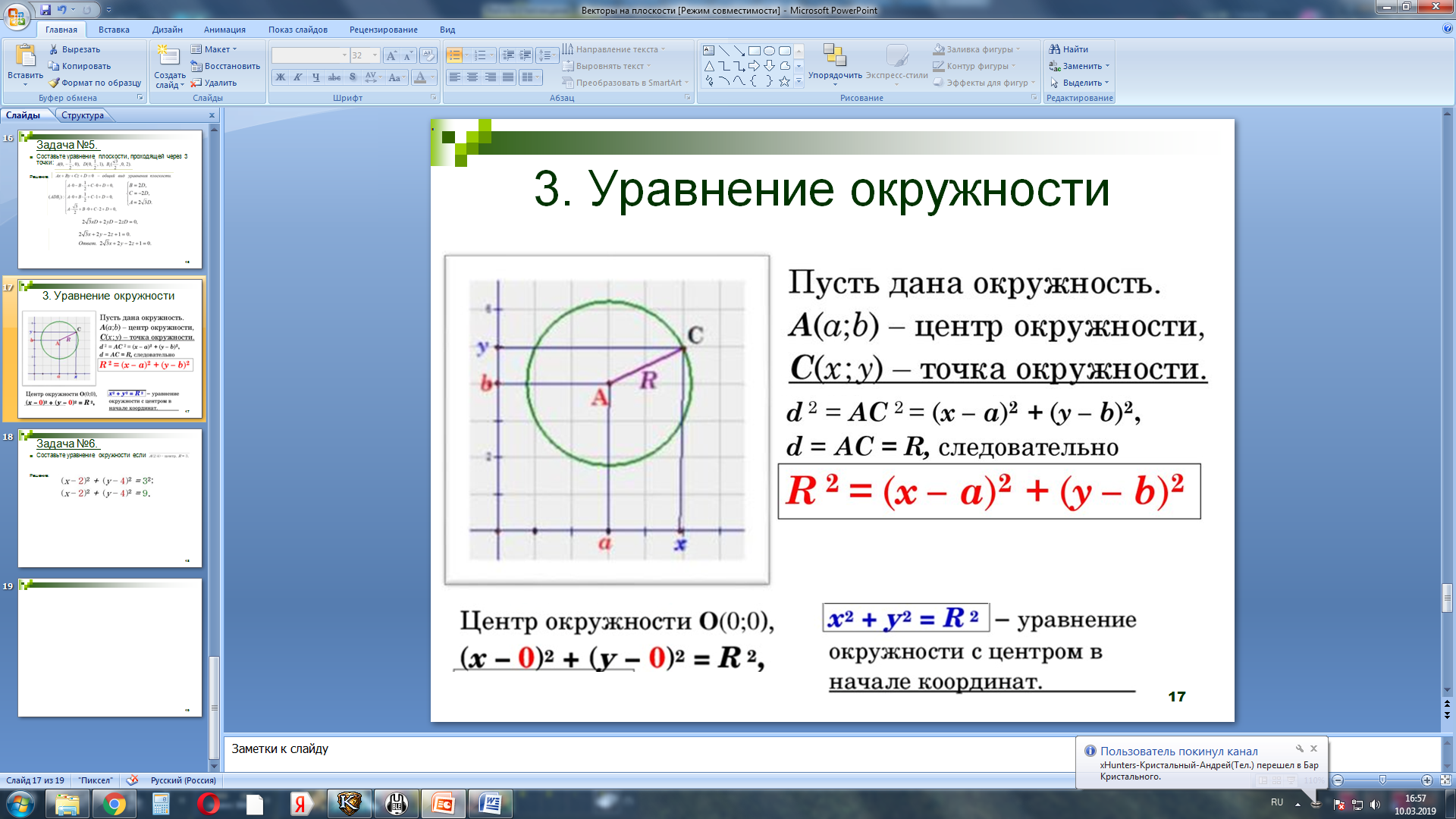
3. Уравнение окружности.
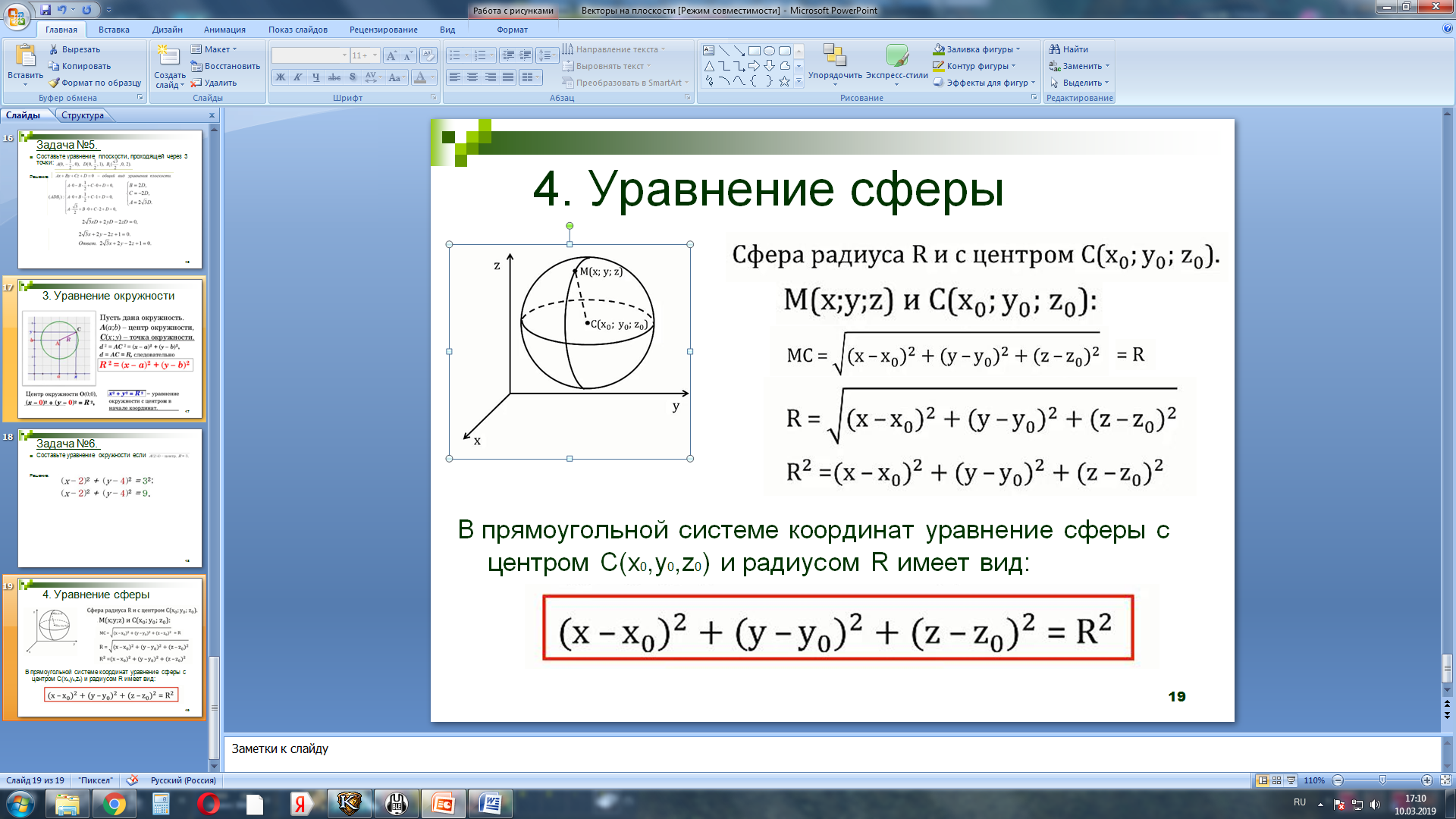
4.Уравнение сферы.
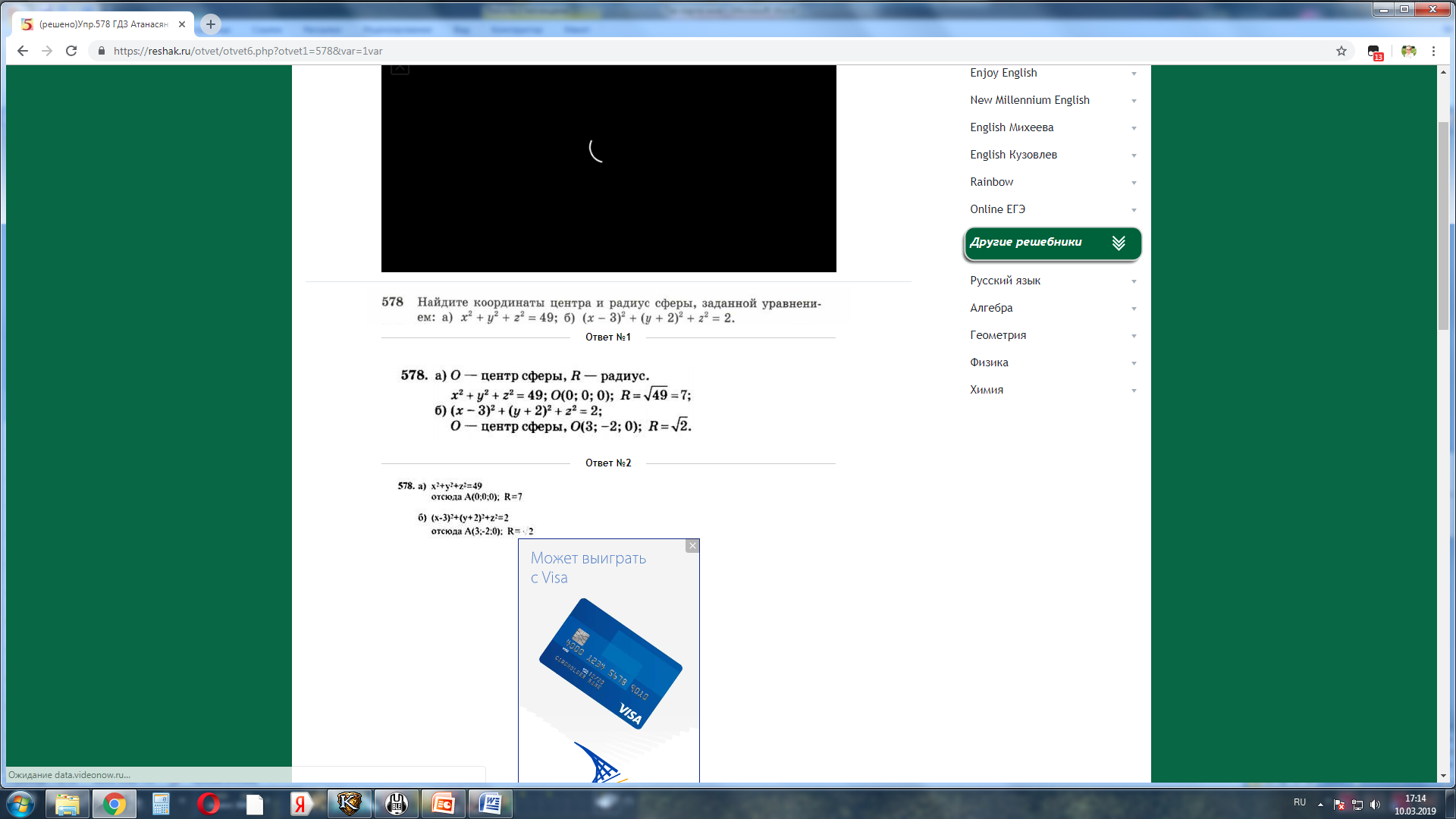
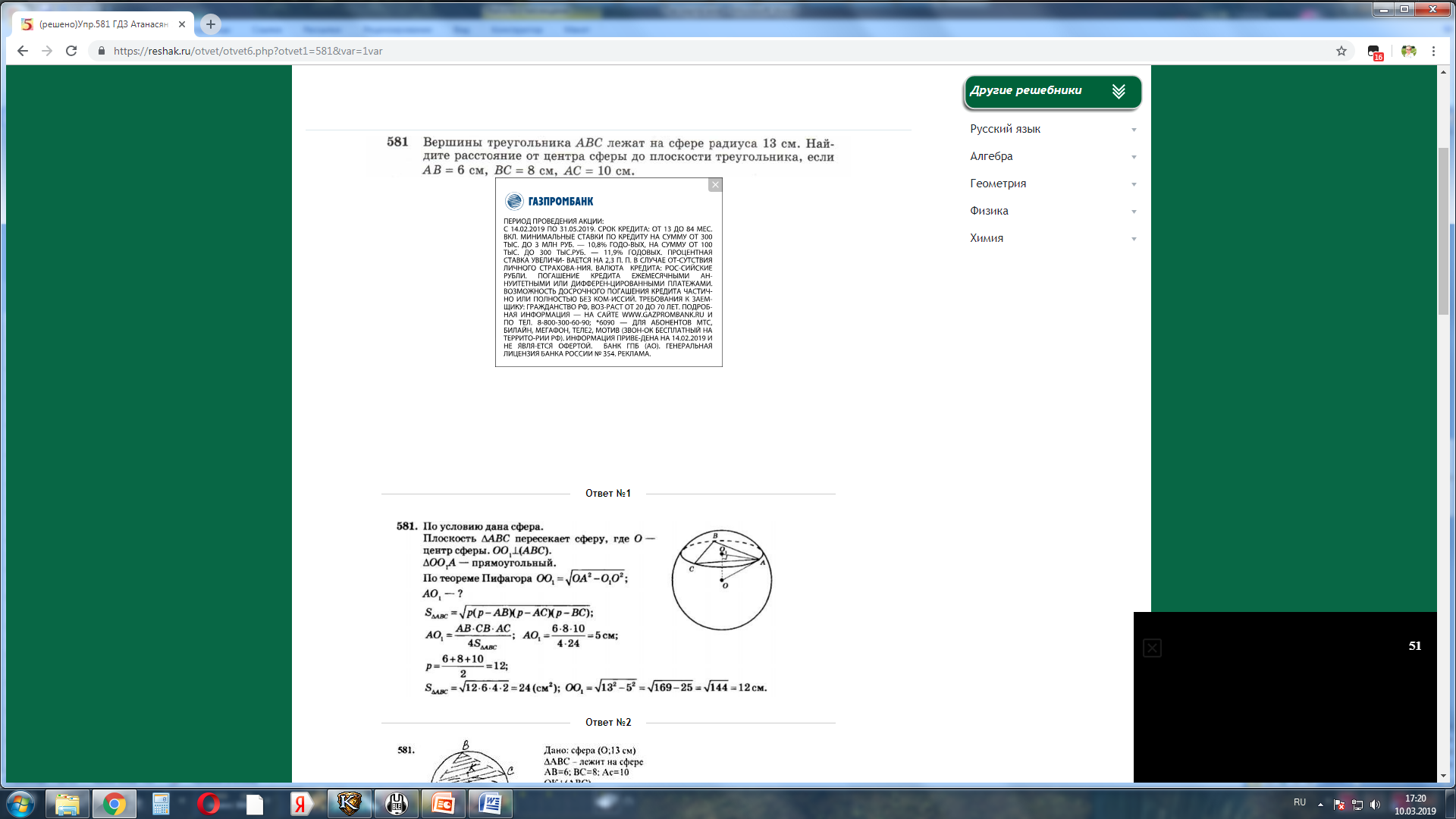
Решение задач: (решаются задачи из учебника (2)



Домашнее задание. Учебник Геометрии 10-11 класс Атанасян п.61 стр 132, №576, №577.
Задание высылать в личном сообщении в вк или на почту SHPAK.IRINA.S@yandex.ru
Перед каждым заданием в тетради пишем ФИО, дата, тема урока