По существу, нужно найти коэффициенты Фурье 
, то есть, составить и вычислить три определённых интеграла.
Пожалуйста, перепишите общий вид ряда Фурье и три рабочие формулы к себе в тетрадь. Я очень рад, что у некоторых посетителей сайта прямо на моих глазах осуществляется детская мечта стать космонавтом =)
Поехали:
Пример 2
Разложить функцию 
в ряд Фурье на промежутке 
. Построить график , график суммы ряда 
и частичной суммы 
.
Решение: первая часть задания состоит в разложении функции в ряд Фурье.
Начало стандартное, обязательно записываем, что:
В данной задаче период разложения 
, полупериод 
.
Разложим функцию в ряд Фурье на промежутке :
Используя соответствующие формулы, найдём коэффициенты Фурье. Теперь нужно составить и вычислить три определённых интеграла. Для удобства я буду нумеровать пункты:
1) Первый интеграл самый простой, однако и он уже требует глаз да глаз:
2) Используем вторую формулу:
Данный интеграл хорошо знаком и берётся он по частям:
При нахождении 
использован метод подведения функции под знак дифференциала.
В рассматриваемом задании сподручнее сразу использовать формулу интегрирования по частям в определённом интеграле 
:
Пара технических замечаний. Во-первых, после применения формулы всё выражение нужно заключить в большие скобки, так как перед исходным интегралом находится константа 
. Не теряем её! Скобки можно раскрыть на любом дальнейшем шаге, я это сделал в самую последнюю очередь. В первом «куске» 
проявляем крайнюю аккуратность в подстановке, как видите, константа 
не при делах, и пределы интегрирования подставляются в произведение 
. Данное действие выделено квадратными скобками. Ну а интеграл 
второго «куска» формулы вам хорошо знаком из тренировочного задания;-)
И самое главное – предельная концентрация внимания!
3) Ищем третий коэффициент Фурье:
Получен родственник предыдущего интеграла, который тоже интегрируется по частям:
Этот экземпляр чуть сложнее, закомментирую дальнейшие действия пошагово:
(1) Выражение 
полностью заключаем в большие скобки. Не хотел показаться занудой, слишком уж часто теряют константу .
(2) В данном случае я немедленно раскрыл эти большие скобки. Особое внимание уделяем первому «куску»: константа 
курит в сторонке и не участвует в подстановке пределов интегрирования (
и 
) в произведение 
. Ввиду загромождённости записи это действие снова целесообразно выделить квадратными скобками. Со вторым «куском» 
всё проще: здесь дробь 
появилась после раскрытия больших скобок, а константа 
– в результате интегрирования знакомого интеграла;-)
(3) В квадратных скобках проводим преобразования 
, а в правом интеграле – подстановку пределов интегрирования.
(4) Выносим «мигалку» из квадратных скобок: 
, после чего раскрываем внутренние скобки: 
.
(5) Взаимоуничтожаем 1 и –1 в скобках и проводим окончательные упрощения.
Наконец-то найдены все три коэффициента Фурье:
Подставим их в формулу :
При этом не забываем разделить 
пополам. На последнем шаге константа («минус два»), не зависящая от «эн», вынесена за пределы суммы.
Таким образом, мы получили разложение функции в ряд Фурье на промежутке :
Изучим вопрос сходимости ряда Фурье. Я объясню теорию, в частности теорему Дирихле, буквально «на пальцах», поэтому если вам необходимы строгие формулировки, пожалуйста, обратитесь к учебнику по математическому анализу (например, 2-й том Бохана; или 3-й том Фихтенгольца, но в нём труднее).
Во второй части задачи требуется изобразить график , график суммы ряда и график частичной суммы .
График функции представляет собой обычную прямую на плоскости, которая проведена чёрным пунктиром:
Разбираемся с суммой ряда . Как вы знаете, функциональные ряды сходятся к функциям. В нашем случае построенный ряд Фурье 
при любом значении «икс» сойдётся к функции , которая изображена красным цветом. Данная функция терпит разрывы 1-го рода в точках 
, но определена и в них (красные точки на чертеже)
Таким образом: 
. Легко видеть, что заметно отличается от исходной функции , именно поэтому в записи ставится значок «тильда», а не знак равенства.
Изучим алгоритм, по которому удобно строить сумму ряда.
На центральном интервале 
ряд Фурье сходится к самой функции (центральный красный отрезок совпадает с чёрным пунктиром линейной функции).
Теперь немного порассуждаем о природе рассматриваемого тригонометрического разложения. В ряд Фурье 
входят только периодические функции (константа, синусы и косинусы), поэтому сумма ряда 
тоже представляет собой периодическую функцию.
Что это значит в нашем конкретном примере? А это обозначает то, что сумма ряда 
– непременно периодична и красный отрезок интервала обязан бесконечно повторяться слева и справа.
Думаю, сейчас окончательно прояснился смысл фразы «период разложения ». Упрощённо говоря, через каждые 
ситуация вновь и вновь повторяется.
На практике обычно достаточно изобразить три периода разложения, как это сделано на чертеже. Ну и ещё «обрубки» соседних периодов – чтобы было понятно, что график продолжается.
Особый интерес представляют точки разрыва 1-го рода. В таких точках ряд Фурье сходится к изолированным значениям, которые расположены ровнёхонько посередине «скачка» разрыва (красные точки на чертеже). Как узнать ординату этих точек? Сначала найдём ординату «верхнего этажа»: для этого вычислим значение функции в крайней правой точке центрального периода разложения: 
. Чтобы вычислить ординату «нижнего этажа» проще всего взять крайнее левое значение этого же периода: 
. Ордината среднего значения – это среднее арифметическое суммы «верха и низа»: 
. Приятным является тот факт, что при построении чертежа вы сразу увидите, правильно или неправильно вычислена середина.
Построим частичную сумму ряда и заодно повторим смысл термина «сходимость». Мотив известен ещё из урока о сумме числового ряда. Распишем наше богатство подробно:
Чтобы составить частичную сумму необходимо записать нулевой + ещё два члена ряда. То есть, 
На чертеже график функции 
изображен зелёным цветом, и, как видите, он достаточно плотно «обвивает» полную сумму . Если рассмотреть частичную сумму из пяти членов ряда 
, то график этой функции будет ещё точнее приближать красные линии, если сто членов 
– то «зелёный змий» фактически полностью сольётся с красными отрезками и т.д. Таким образом, ряд Фурье сходится к своей сумме .
Интересно отметить, что любая частичная сумма 
– это непрерывная функция, однако полная сумма ряда всё же разрывна.
На практике не так уж редко требуется построить и график частичной суммы. Как это сделать? В нашем случае необходимо рассмотреть функцию на отрезке , вычислить её значения на концах отрезка и в промежуточных точках (чем больше точек рассмотрите – тем точнее будет график). Затем следует отметить данные точки на чертеже и аккуратно изобразить график на периоде , после чего «растиражировать» его на соседние промежутки. А как иначе? Ведь приближение – это тоже периодическая функция… …чем-то мне её график напоминает ровный ритм сердца на дисплее медицинского прибора.
Выполнять построение, конечно, не сильно удобно, так как 
и приходится проявлять сверхаккуратность, выдерживая точность не меньше, чем до половины миллиметра. Впрочем, читателей, которые не в ладах с черчением, обрадую – в «реальной» задаче выполнять чертёж нужно далеко не всегда, где-то в 50% случаев требуется разложить функцию в ряд Фурье и всё.
После выполнения чертежа завершаем задание:
Ответ:
Во многих задачах функция терпит разрыв 1-го рода прямо на периоде разложения:
Пример 3
Разложить в ряд Фурье функцию 
, заданную на отрезке . Начертить график функции и полной суммы ряда.
Предложенная функция задана кусочным образом (причём, заметьте, только на отрезке ) и терпит разрыв 1-го рода в точке 
. Можно ли вычислить коэффициенты Фурье? Без проблем. И левая 
и правая 
части функции интегрируемы на своих промежутках, поэтому интегралы в каждой из трёх формул следует представить в виде суммы двух интегралов. Посмотрим, например, как это делается у нулевого коэффициента:
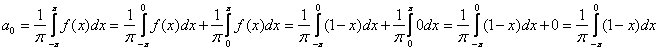
Второй интеграл оказался равным нулю, что убавило работы, но так бывает далеко не всегда.
Аналогично расписываются два других коэффициента Фурье.
Как изобразить сумму ряда? На левом интервале 
чертим отрезок прямой , а на интервале 
– отрезок прямой (жирно-жирно выделяем участок оси 
). То есть, на промежутке разложения сумма ряда совпадает с функцией везде, кроме трёх «нехороших» точек. В точке разрыва функции ряд Фурье сойдётся к изолированному значению, которое располагается ровно посередине «скачка» разрыва. Его нетрудно увидеть и устно: левосторонний предел: 
, правосторонний предел: 
и, очевидно, что ордината средней точки равна 0,5.
В силу периодичности суммы , картинку необходимо «размножить» на соседние периоды, в частности изобразить то же самое на интервалах 
и 
. При этом, в точках ряд Фурье сойдётся к срединным значениям.
По сути-то ничего нового здесь нет.
Постарайтесь самостоятельно справиться с данной задачей. Примерный образец чистового оформления и чертёж в конце урока.
Далее возникает закономерный вопрос: если схема работает на отрезке , то почему бы её не применить к разложению функций в ряд Фурье на промежутках 
или на каком-нибудь другом периоде?