п. 4.1. Формула Бернулли
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться, либо не появиться. Если вероятность события А в каждом испытании одна и та же и не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Разберём следующий пример.
Стрелок совершает 4 выстрела по мишени. Вероятность попадания при каждом выстреле постоянна и равна p. Найти вероятность того, что:
а) стрелок попадёт только один раз; б) стрелок попадёт 2 раза; в) стрелок попадёт три раза.
Решение. а) _____________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
б) ____________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
в) ____________________________________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
В общем случае, вероятность сложного события, состоящего в том, что в n испытаниях событие А появится k раз и не появится (n – k) раз, вычисляется, как:
 .
.
Полученную формулу называют ______________________________________,
а коэффициент  часто называют _________________________________________.
часто называют _________________________________________.
Пример. Вероятность того, что в анкете будет дан отрицательный ответ, равна 0,2. Найти вероятность того, что в пяти проверенных анкетах отрицательный ответ будет дан три раза.
Решение. ________________________________________________________________
______________________________________________________________________________
п. 4.2. Наивероятнейшее число появления события в независимых испытаниях
Иногда требуется знать, какое число наступлений события А является наивероятнейшим, то есть при каком числе  вероятность
вероятность  – наибольшая.
– наибольшая.
Определение. ____________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Получить формулу для определения наивероятнейшего числа можно с помощью формулы Бернулли (см. Приложение). Опустив здесь выкладки, перепишем готовый результат:
 (2)
(2)
Найдём длину интервала, определяемого неравенством (2), для чего вычтем из его большей границы меньшую:
 . (3)
. (3)
Учитывая, что событие может произойти в n испытаниях только целое число раз, и полученный результат (3), можем заключить, что:
а) если число np – q - дробное, то существует одно наивероятнейшее число k 0;
б) если число np – q - целое, то существует два наивероятнейших
числа, а именно: k 0 и k 0 + 1;
в) если число np – целое, то наивероятнейшее число k 0 = np.
Пример. Вероятность того, что при броске мяча баскетболист попадёт в корзину, равна 0,3. Найти наивероятнейшее число попаданий при 8 бросках и соответствующую вероятность.
Решение. Из условия: всего бросков п = ____; вероятность попадания в корзину при каждом броске р = ____. Вероятность промаха при каждом броске q = ______. Тогда, из неравенства (2) получаем наивероятнейшее количество попаданий при 8 бросках:
_____________  ______________ или _____
______________ или _____ 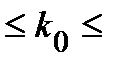 _____
_____
Поскольку левая граница – дробное число, то существует единственное наивероятнейшее значение, и, очевидно, что оно равно ________.
п. 4.3. Определение вероятности события при большом числе испытаний
При больших значениях n и дробных вероятностях p и q пользоваться формулой Бернулли становиться довольно трудно. В этих случаях используют другие методы расчёта, которые позволяют приближенно найти вероятность появления события А.
| Локальная формула Лапласа | Интегральная формула Лапласа | Формула Пуассона | |
| Условия применения | ______________________________________ ______________________________________ ______________________________________ ______________________________________ | ______________________________________ ______________________________________ ______________________________________ ______________________________________ | ______________________________________ ______________________________________ ______________________________________ ______________________________________ |
| Формулировка теоремы | ______________________________________ ______________________________________ ______________________________________ ______________________________________ ______________________________________ ______________________________________ ______________________________________ | ______________________________________ ______________________________________ ______________________________________ ______________________________________ ______________________________________ ______________________________________ ______________________________________ | ______________________________________ ______________________________________ ______________________________________ ______________________________________ ______________________________________ ______________________________________ ______________________________________ |
| Формулы | |||
| Примеры | Пример. Вероятность того, что в анкете будет дан отрицательный ответ равна 0,2. Найти вероятность того, что среди 100 случайно отобранных анкет 75 будет с положительным ответом.
Решение.  ; ;

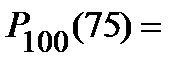
| Пример. Вероятность того, что в анкете будет дан отрицательный ответ равна 0,2. Найти вероятность того, что среди 100 случайно отобранных анкет будет не менее 75 с положительным ответом.
Решение.
 


| Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что во время транспортировки изделие повредится, равно 0,0002. Найти вероятность, что на базу прибудут 3 негодных изделия.
Решение. n = _____, p = ______, k = ___. Найдем  : :
 ___________.
По формуле Пуассона искомая вероятность приближенно равна ___________.
По формуле Пуассона искомая вероятность приближенно равна

|
ПРИЛОЖЕНИЕ
Таблица 1.
Значения функции 
| х | ||||||||||
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 4,0 | 0,3989 | 0,3989 | 0,3989 | 0,3988 | 0,3986 | 0,3984 | 0,3982 | 0,3980 | 0,3977 | 0,3973 |
Таблица 2.
Значения функции 
| х | Ф(х) | х | Ф(х) | х | Ф(х) | х | Ф (х) | |
| 0,00 | 0,0000 | 0,31 | 0,1217 | 0,62 | 0,2324 | 0,93 | 0,3238 | |
| 0,01 | 0,0040 | 0,32 | 0,1255 | 0,63 | 0,2357 | 0,94 | 0,3264 | |
| 0,02 | 0,0080 | 0,33 | 0,1293 | 0,64 | 0,2389 | 0,95 | 0,3289 | |
| 0,03 | 0,0120 | 0,34 | 0,1331 | 0,65 | 0,2422 | 0,96 | 0,3315 | |
| 0,04 | 0,0160 | 0,35 | 0,1368 | 0,66 | 0,2454 | 0,97 | 0,3340 | |
| 0,05 | 0,0199 | 0,36 | 0,1406 | 0,67 | 0,2486 | 0,98 | 0,3365 | |
| 0,06 | 0,0239 | 0,37 | 0,1443 | 0,68 | 0,2517 | 0,99 | 0,3389 | |
| 0,07 | 0,0279 | 0,38 | 0,1480 | 0,69 | 0,2549 | 1,00 | 0,3413 | |
| 0,08 | 0,0319 | 0,39 | 0,1517 | 0,70 | 0,2580 | 1,01 | 0,3438 | |
| 0,09 | 0,0359 | 0,40 | 0,1554 | 0,71 | 0,2611 | 1,02 | 0,3461 | |
| 0,10 | 0,0398 | 0,41 | 0,1591 | 0,72 | 0,2642 | 1,03 | 0,3485 | |
| 0,11 | 0,0438 | 0,42 | 0,1628 | 0,73 | 0,2673 | 1,04 | 0,3508 | |
| 0,12 | 0,0478 | 0,43 | 0,1664 | 0,74 | 0,2703 | 1,05 | 0,3531 | |
| 0,13 | 0,0517 | 0,44 | 0,1700 | 0,75 | 0,2734 | 1,06 | 0,3554 | |
| 0,14 | 0,0557 | 0,45 | 0,1736 | 0,76 | 0,2764 | 1,07 | 0,3577 | |
| 0,15 | 0,0596 | 0,46 | 0,1772 | 0,77 | 0,2794 | 1,08 | 0,3599 | |
| 0,16 | 0,0636 | 0,47 | 0,1808 | 0,78 | 0,2823 | 1,09 | 0,3621 | |
| 0,17 | 0,0675 | 0,48 | 0,1844 | 0,79 | 0,2852 | 1,10 | 0,3643 | |
| 0,18 | 0,0714 | 0,49 | 0,1879 | 0,80 | 0,2881 | 1,11 | 0,3665 | |
| 0,19 | 0,0753 | 0,50 | 0,1915 | 0,81 | 0,2910 | 1,12 | 0,3686 | |
| 0,20 | 0,0793 | 0,51 | 0,1950 | 0,82 | 0,2939 | 1,13 | 0,3708 | |
| 0,21 | 0,0832 | 0,52 | 0,1985 | 0,83 | 0,2967 | 1,14 | 0,3729 | |
| 0,22 | 0,0871 | 0,53 | 0,2019 | 0,84 | 0,2995 | 1,15 | 0,3749 | |
| 0,23 | 0,0910 | 0,54 | 0,2054 | 0,85 | 0,3023 | 1,16 | 0,3770 | |
| 0,24 | 0,0948 | 0,55 | 0,2088 | 0,86 | 0,3051 | 1,17 | 0,3790 | |
| 0,25 | 0,0987 | 0,56 | 0,2123 | 0,87 | 0,3078 | 1,18 | 0,3810 | |
| 0,26 | 0,1026 | 0,57 | 0,2157 | 0,88 | 0,3106 | 1,19 | 0,3830 | |
| 0,27 | 0,1064 | 0,58 | 0,2190 | 0,89 | 0,3133 | 1,20 | 0,3849 | |
| 0,28 | 0,1103 | 0,59 | 0,2224 | 0,90 | 0,3159 | 1,21 | 0,3869 | |
| 0,29 | 0,1141 | 0,60 | 0,2257 | 0,91 | 0,3186 | 1,22 | 0,3883 | |
| 0,30 | 0,1179 | 0,61 | 0,2291 | 0,92 | 0,3212 | 1,23 | 0,3907 | |
Продолжение таблицы 2.
| х | Ф(х) | х | Ф(х) | х | Ф(х) | х | Ф (х) | |
| 1,24 | 0,3925 | 1,58 | 0,4429 | 1,92 | 0,4726 | 2,52 | 0,4941 | |
| 1,25 | 0,3944 | 1,59 | 0,4441 | 1,93 | 0,4732 | 2,54 | 0,4945 | |
| 1,26 | 0,3962 | 1,60 | 0,4452 | 1,94 | 0,4738 | 2,56 | 0,4948 | |
| 1,27 | 0,3980 | 1,61 | 0,4463 | 1,95 | 0,4744 | 2,58 | 0,4951 | |
| 1,28 | 0,3997 | 1,62 | 0,4474 | 1,96 | 0,4750 | 2,60 | 0,4953 | |
| 1,29 | 0,4015 | 1,63 | 0,4484 | 1,97 | 0,4756 | 2,62 | 0,4956 | |
| 1,30 | 0,4032 | 1,64 | 0,4495 | 1,98 | 0,4761 | 2,64 | 0,4959 | |
| 1,31 | 0,4049 | 1,65 | 0,4505 | 1,99 | 0,4767 | 2,66 | 0,4961 | |
| 1,32 | 0,4066 | 1,66 | 0,4515 | 2,00 | 0,4772 | 2,68 | 0,4963 | |
| 1,33 | 0,4082 | 1,67 | 0,4525 | 2,02 | 0,4783 | 2,70 | 0,4965 | |
| 1,34 | 0,4099 | 1,68 | 0,4535 | 2,04 | 0,4793 | 2,72 | 0,4967 | |
| 1,35 | 0,4115 | 1,69 | 0,4545 | 2,06 | 0,4803 | 2,74 | 0,4969 | |
| 1,36 | 0,4131 | 1,70 | 0,4554 | 2,08 | 0,4812 | 2,76 | 0,4971 | |
| 1,37 | 0,4147 | 1,71 | 0,4564 | 2,10 | 0,4821 | 2,78 | 0,4973 | |
| 1,38 | 0,4162 | 1,72 | 0,4573 | 2,12 | 0,4830 | 2,80 | 0,4974 | |
| 1,39 | 0,4177 | 1,73 | 0,4582 | 2,14 | 0,4838 | 2,82 | 0,4976 | |
| 1,40 | 0,4192 | 1,74 | 0,4591 | 2,16 | 0,4846 | 2,84 | 0,4977 | |
| 1,41 | 0,4207 | 1,75 | 0,4599 | 2,18 | 0,4854 | 2,86 | 0,4979 | |
| 1,42 | 0,4222 | 1,76 | 0,4608 | 2,20 | 0,4861 | 2,88 | 0,4980 | |
| 1,43 | 0,4236 | 1,77 | 0,4616 | 2,22 | 0,4868 | 2,90 | 0,4981 | |
| 1,44 | 0,4251 | 1,78 | 0,4625 | 2,24 | 0,4875 | 2,92 | 0,4982 | |
| 1,45 | 0,4265 | 1,79 | 0,4633 | 2,26 | 0,4881 | 2,94 | 0,4984 | |
| 1,46 | 0,4279 | 1,80 | 0,4641 | 2,28 | 0,4887 | 2,96 | 0,4985 | |
| 1,47 | 0,4292 | 1,81 | 0,4649 | 2,30 | 0,4893 | 2,98 | 0,4986 | |
| 1,48 | 0,4306 | 1,82 | 0,4656 | 2,32 | 0,4898 | 3,00 | 0,49865 | |
| 1,49 | 0,4319 | 1,83 | 0,4664 | 2,34 | 0,4904 | 3,20 | 0,49931 | |
| 1,50 | 0,4332 | 1,84 | 0,4671 | 2,36 | 0,4909 | 3,40 | 0,49966 | |
| 1,51 | 0,4345 | 1,85 | 0,4678 | 2,38 | 0,4913 | 3,60 | 0,499841 | |
| 1,52 | 0,4357 | 1,86 | 0,4686 | 2,40 | 0,4918 | 3,80 | 0,499928 | |
| 1,53 | 0,4370 | 1,87 | 0,4693 | 2,42 | 0,4922 | 4,00 | 0,499968 | |
| 1,54 | 0 4382 | 1,88 | 0,4690 | 2,44 | 0,4927 | 4,50 | 0,499997 | |
| 1,55 | 0,4394 | 1,89 | 0,4706 | 2,46 | 0,4931 | 5,00 | 0,49999997 | |
| 1,56 | 0,4406 | 1,90 | 0,4713 | 2,48 | 0,4934 | ¥ | 0,5 | |
| 1,57 | 0,4418 | 1,91 | 0,4719 | 2,50 | 0,4938 | |||
Таблица 3.
Распределение Пуассона 
т – число появлений события в п независимых испытаниях,
а = тр – среднее число появлений события в п испытаниях.
| а т | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| — | — | — | ||||||||
| — | — | — | — | — | — | |||||
| — | — | — | — | — | — | — | — | — |
| а т | 1,1 | 1,2 | 1,3 | 1, 4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 |
| — | — | |||||||||
| — | — | — | — | — | — |
| а т | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 |
Продолжение табл.3.
| а т | 3,5 | 4,0 | 4,5 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 | 10,0 | 11,0 |
| — — — — — — — — — — — — — | — — — — — — — — — — — — | — — — — — — — — — — — | — — — — — — — — — — — | — — — — — — — — — | — — — — — — — | — — — — — | — — — — | - — — | - — |
Примечание. В таблице даны значения вероятности  после запятой.
после запятой.