Важность байесовской переоценки вероятностей (гипотез) можно понять на следующем примере.

Тема 3. СЛЕДСТВИЯ ТЕОРЕМ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ

п. 3.1. Формула полной вероятности

Постановка задачи._____________________________

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

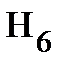
Теорема 1.1. (формула полной вероятности). Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий , , …, , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

Замечание (о гипотезах). Несовместные события 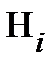, где , в контексте использования формулы полной вероятности называют гипотезами, на что и указывает их запись с помощью буквы Н – от «hypothesis».

Пример. В комиссию по проведению референдума поступили бюллетени с двух участков. С первого участка поступило 1000 бюллетеней, со второго – 3000. Среди бюллетеней первого участка 100 недействительных бюллетеней, среди бюллетеней второго участка 200 недействительных. При подсчете голосов наудачу взят бюллетень. Найти вероятность того, что он является действительным (событие А).

Решение. Пустьсобытие Н₁ – бюллетень поступил с 1-го участка, событие Н₂ – бюллетень поступил со 2-го участка. Находим вероятности данных гипотез:

Находим условные вероятности «__________________________________________________

_________________________

По формуле полной вероятности окончательно получаем:

п. 3.2. Вероятности гипотез. Формула Байеса

Пусть событие А может наступить при условии появления одного из несовместных событий (гипотез) Н₁, Н₂,..., Н_n, образующих полную группу. Вероятность появления такого события А определяется по формуле полной вероятности:

. (1)

Допустим, что произведено испытание, в результате которого событие А появилось. Как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез? Для ответа на этот вопрос нам потребуется найти условные вероятности .

Найдем сначала условную вероятность . По теореме умножения имеем:

Отсюда

Подставив сюда Р(А) из равенства (1), получим:

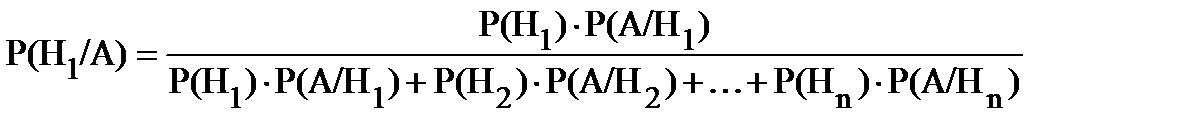Аналогично можно вывести условные вероятности остальных гипотез, то есть условная вероятность любой гипотезы H _i (i = 1, 2,..., n) может быть вычислена, как:

Полученные формулы называют формулами Байеса (по имени английского математика). Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А. Таким образом, в задачах на формулы Байеса в условии обязательно фигурирует некое произошедшее событие.

- априорные (оцененные до испытания) вероятности; - апостериорные (оцененные после испытания) вероятности.

Апостериорные вероятности - вероятности тех же гипотез, пересчитанные в связи «со вновь открывшимися обстоятельствами » – с учётом того факта, что событие А достоверно произошло.

Важность байесовской переоценки вероятностей (гипотез) можно понять на следующем примере.

Задача. Среди определенной группы людей вероятность некоторой болезни 0,02. Тест, позволяющий выявить болезнь, несовершенен. На больном он дает позитивный результат в 98 случаях из 100, и, кроме того, он дает позитивный результат в 4 случаях из

100 на здоровом. Найдите вероятность того, что человек, на котором тест дал положительный результат, действительно болен.

Решение. Введём обозначения следующих событий и гипотез:

Н_{1 -}__________________________________________________________________________ Н_{2 -}__________________________________________________________________________

А - __________________________________________________________________________

Важность байесовской переоценки вероятностей (гипотез) можно понять на следующем примере.

Поиск по сайту