Филиал федерального государственного бюджетного образовательного
Учреждения высшего профессионального образования «Сочинский
Государственный университет» в г. Нижний Новгород
Нижегородской области
Факультет Менеджмента
Кафедра Экономики и туризма
КОНТРОЛЬНАЯ РАБОТА
Дисциплина Теория оптимального управления
Выполнила студентка 4 курс ЗФО
Группа МГБ-41-09
Буткеева Юлия Валерьевна
Проверил Преподаватель
Радостин Андрей Викторович
Нижний Новгород - 2013
Задание №1
Решить линейную производственную задачу симплексным методом, взяв исходные данные из таблицы, где технологическая матрица А затрат различных ресурсов на единицу каждой продукции, вектор объёмов ресурсов В и вектор удельной прибыли С при возможном выпуске четырёх видов продукции с использованием трёх видов ресурсов
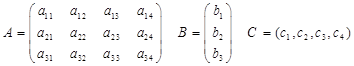компактно записаны в виде
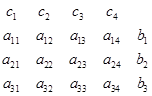
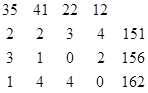
Решение:
Запишем целевую функцию и систему неравенств-ограничений, используя данные задачи:
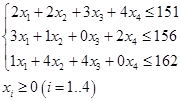
Для решения задачи симплексным методом введём новые переменные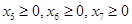 
и перейдем к системе равенств:
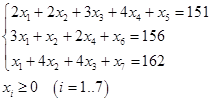
шаг.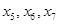 
- основные переменные,
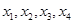- неосновные переменные.
Выразим основные переменные через неосновные:
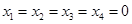Þ 
.
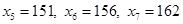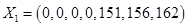- базисное решение, 
.
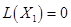Чтобы увеличить значение целевой функции, переведём в основные переменные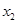 
, т.к. она входит в целевую функцию с наибольшим коэффициентом (41).
.
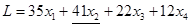Полагая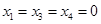 
и учитывая, что 
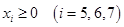, получаем ограничения на рост значения переменной :
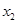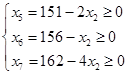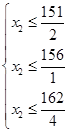Þ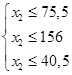 
Þ 
Þ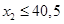 
.
Решением системы является решение последнего неравенства, следовательно, последнее уравнение - разрешающее, переменную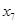 
переводим в неосновные.
|
|
шаг.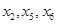 
- основные переменные,
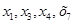- неосновные переменные.
.
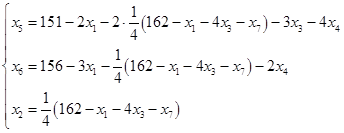
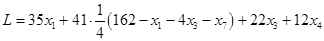Или
.
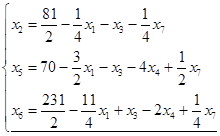
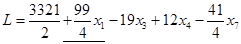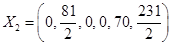- второе базисное решение, 
.
Значение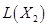 
не является максимальным, т.к. переменные 
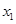и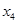 
входят в выражение для целевой функции с положительными коэффициентами. Переведём 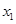в основные переменные.
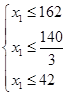Þ 
Þ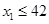 
.
Третье уравнение - разрешающее, переменную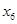 
переводим в неосновные.
шаг.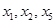 
- основные переменные,
- неосновные переменные.
.
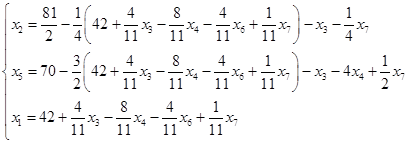
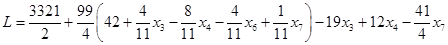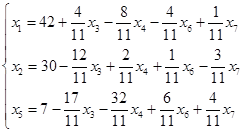
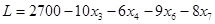- это выражение не содержит положительных коэффициентов при неосновных переменных, следовательно, достигнут максимум целевой функции.
, 
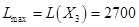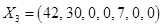
Ответ: для получения максимальной прибыли необходимо выпускать 42 единицы продукции I вида и 30 единиц продукции II вида, при этом прибыль составит 2700 ден. ед.
Задание №2
транспортный линейный программирование поставщик
Решить транспортную задачу линейного программирования.
Решение: сравним мощности поставщиков и потребителей:
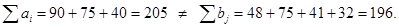
открытая модель транспортной задачи. Введём фиктивного потребителя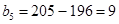 
, стоимость перевозок к нему положим равными нулю.
| b a | |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| * | |||||||||||
    
|
|
|
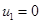
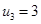
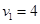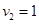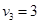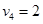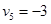
Выполним первое распределение поставок:
Число заполненных клеток должно быть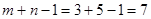 
. Условие выполняется.
Суммарные затраты на перевозку при полученном плане:
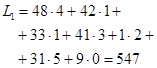(усл.ден.ед.)
Составим оценки 
для заполненных клеток таблицы, из условия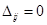 
определим 
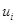и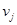 
.
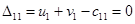
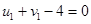Положим , тогда
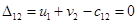
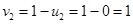
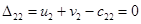
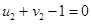
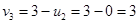
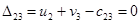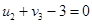Þ 
Þ 
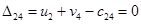
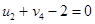
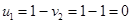
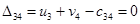
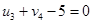
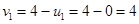
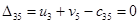
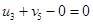
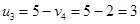
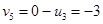
Определим оценки незаполненных клеток:
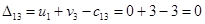
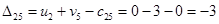
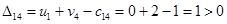
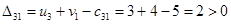
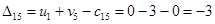
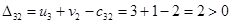
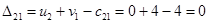
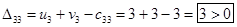
Имеем 4 положительные оценки, т.е, построенный план распределения поставок не является оптимальным и допускает улучшение. Переведём поставку в клетку с наибольшей оценкой: (3,3). Будут задействованы клетки (2,3), (2,4), (3,4).
Таким образом, величина передвигаемой поставки х=31.
Получаем второе распределение поставок:
| 41- х | 1+ х |
| х | 31- х |
| b a | |||||||||||
|
| |||||||||||
| * | |||||||||||
|
| |||||||||||
| |||||||||||
  
|
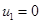
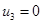
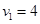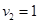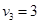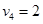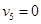
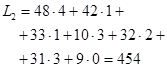(усл.ден.ед.)
| 42- х | х |
| 33 +х | 32- х |
Пересчитываем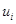 
и 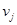и находим оценки свободных клеток:
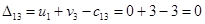
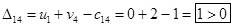
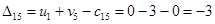
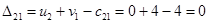
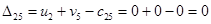
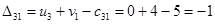
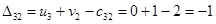
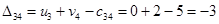
Есть одна положительная оценка, следовательно, продолжаем улучшать план распределения, переводя поставку в клетку (1,4). Задействуем также клетки (1,2), (2,2), (2,4).
х=32.
Получаем третье распределение поставок:
| b a | |||||||||||
|
| |||||||||||
| * | |||||||||||
|
| |||||||||||
|
| |||||||||||
|
|
|
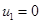
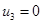
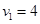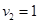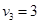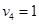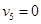
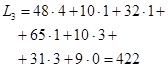(усл.ден.ед.)
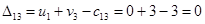
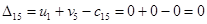
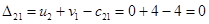
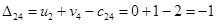
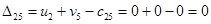
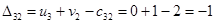
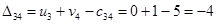
Положительных оценок нет, следовательно, получено оптимальное распределение поставок, при котором затраты на перевозку будут минимальны и составят 422 усл.ден.ед.
Однако четыре клетки имеют нулевую оценку. Это означает, что существуют альтернативные оптимальные распределения поставок, при которых затраты на перевозку также будут минимальны. Найдём их, переведя поставку сначала в клетку (1,3).
х=10.
| 10- х | х |
| 65 +х | 10- х |
Так как при переводе 10 ед. товара занулятся одновременно две клетки таблицы (1,2) и (2,3), для сохранения числа заполненных клеток дадим нулевую поставку, например, в клетку (1,2).
| b a | |||||||||||
|
| |||||||||||
| * | |||||||||||
|
| |||||||||||
|
| |||||||||||
|
|
Четвёртое распределение поставок:
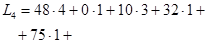
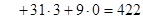(усл.ден.ед.)
Переведём поставку в клетку (1,5)
[-(1,3)-(3,3)-(3,5)].
| 10- х | х |
| 31 +х | 9- х |
х=9.
Пятое распределение поставок:
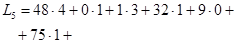
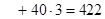(усл.ден.ед.)
Переведём поставку в клетку (2,1)
| b a | |||||||||||
| * | |||||||||||
[-(1,1)-(1,2)-(2,1)].
х=48.
Шестое распределение поставок:
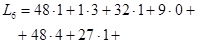
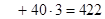(усл.ден.ед.)
| b a | |||||||||||
| * | |||||||||||
Переведём поставку в клетку (2,5)
| 48+ х | 9- х |
| 27- х | х |
[-(1,5) -(1,2)-(2,2)].
х=9.
Седьмое распределение поставок:
| b a | |||||||||||
Ответ: существует 5 оптимальных распределений поставок
, 
, 
,
, 
,
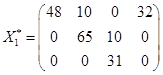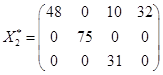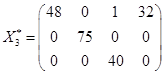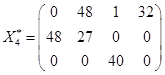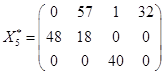при которых расходы на перевозку минимальны и составляют 422 усл. ден.ед.
Задание №3. Решить задачу о распределении ресурсов
Необходимо распределить 500 ден. ед. на три предприятия, прибыль приведена в таблице.
| хj | ||||||
| h1 (xj) | ||||||
| h2 (xj) | ||||||
| h3 (xj) |
Решение.
Обозначим через хj (j = 1,2,3) - количество средств, инвестируемых в j-ое предприятие,
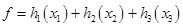- суммарная прибыль.
Требуется найти такие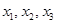 
, что 
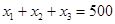и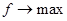 
.
Процесс распределения средств рассматриваем как 3-шаговый, номер шага совпадает с номером предприятия. Выбор переменных 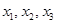- управление на j-ом шаге (j = 1,2,3).
Пусть s - объём средств, имеющихся в наличии перед данным шагом и характеризующих состояние системы на каждом шаге.
В соответствии с принципом оптимальности Беллмана, управление (решение) на каждом шаге нужно выбирать так, чтобы суммарная прибыль была оптимальной на всех оставшихся до конца процесса шагах, включая прибыль на данном шаге. Основное функциональное уравнение примет вид
.
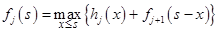Динамическое программирование разворачивается от конца к началу, т.е. сначала планируется последний шаг. На каждом шаге необходимо делать все возможные предположения о том, чем закончился предыдущий шаг.
Шаг 3. Все средства, оставшиеся к третьему шагу, следует вложить в третье предприятие. При этом для возможных значений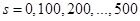 
, получим 
.
 
| |
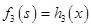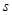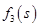
Шаг 2. Распределяем средства между вторым и третьем предприятиями. Делаем все предположения относительно остатка средств s ко второму шагу. После выбора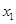 
s также может принимать значения 
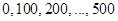. В зависимости от этого выбираем х, находим 
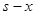и определяем 
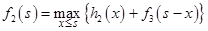. Значения 
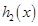берём их исходной таблицы данных, значения 
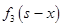- из таблицы шага 1.
Заполним таблицу для различных состояний s.
   
| ||||||
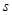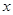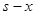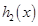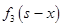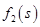
Шаг 1. Кредит первому, второму и третьему предприятиям. Состояние системы перед первым шагом s = 500, т.к. необходимо распределить все имеющиеся средства на три предприятия. Расчёты проводим по формуле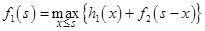 
. Значения 
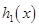берём их исходной таблицы данных, значения 
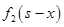- из таблицы шага 2.
  
| ||||||
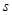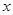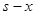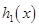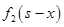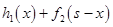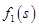
Таким образом, максимальная суммарная прибыль составляет 34 ден. ед.
Она получена на шаге 1 в трёх вариантах:
) как 0 + 34, т.е. прибыль в 0 ден. ед. соответствует выделению 0 ден. ед. первому предприятию. Из шага 2 суммарная прибыль 34 ден. ед. получена в двух случаях:
1.1) 34 = 13 + 21, т.е. прирост 13 ден. ед. соответствует выделению второму предприятию 200 ден. ед. На шаге 1 прирост 21 ден. ед. получен при выделении 300 ден. ед. третьему предприятию. Получаем первое решение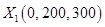 
.
) 34 = 18 + 16, т.е. прирост 18 ден. ед. соответствует выделению второму предприятию 300 ден. ед. На шаге 1 прирост 16 ден. ед. получен при выделении 200 ден. ед. третьему предприятию. Получаем второе решение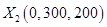 
.
) 34 = 5 + 29, т.е. прибыль в 5 ден. ед. соответствует выделению 100 ден. ед. первому предприятию. Из шага 2 суммарная прибыль 29 ден. ед. получена в двух случаях:
) 29 = 8 + 21, т.е. прирост 8 ден. ед. соответствует выделению второму предприятию 100 ден. ед. На шаге 1 прирост 21 ден. ед. получен при выделении 300 ден. ед. третьему предприятию. Получаем третье решение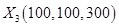 
.
) 29 = 13 + 16, т.е. прирост 13 ден. ед. соответствует выделению второму предприятию 200 ден. ед. На шаге 1 прирост 16 ден. ед. получен при выделении 200 ден. ед. третьему предприятию. Получаем четвёртое решение 
.
) 34 = 10 + 24, т.е. прибыль в 10 ден. ед. соответствует выделению 200 ден. ед. первому предприятию. Из шага 2 суммарная прибыль 24 ден. ед. получена как 8 + 16, что соответствует выделению 100 ден. ед. второму предприятию и 200 ден. ед. третьему предприятию. Пятое решение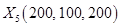 
.