Реальное дифференцирующее звено
Цель лекции: изучить реальные дифференцирующее звено систем автоматического управления, изучить порядок построения АЧХ, ЛАЧХ дифференцирующего звена.
Задачи лекции:
1. Рассмотреть построение реализации дифференцирующего звена.
2. Изучить порядок построения АЧХ, ЛАЧХ дифференцирующего звена
Уравнение этого звена имеет вид:
где T – постоянная времени; K – коэффициент усиления звена.
Реальное дифференцирующее звено с передаточной функцией
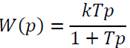
На структурной схеме может быть представлено одним звеном, последовательным соединением инерционного и идеального дифференцирующего звеньев, а также параллельным соединением пропорционального и инерционного звеньев со встречным
сложением сигналов
Амплитудно-фазовая частотная характеристика реального дифференцирующего звена – это окружность, расположенная в первом квадранте, концы диаметра которой, как и у инерционного звена, лежат на действительной оси в точках с координатами U = 0, U = k.
Построим АФЧХ реального дифференцирующего звена.
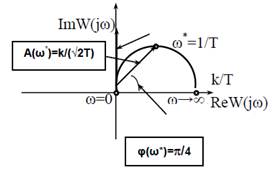
Годограф описывает полуокружность с радиусом, стремящимся к 
при T стремящимся к 0.
Частота ω =1/T считается максимальной, при которой реальное дифференцирующее звено работает "почти как идеальное".
При достаточно низких частотах реальное дифференцирующее звено близко к идеальному.
График асимптотической ЛАЧХ реального дифференцирующего звена составлен из двух полупрямых, которые пересекаются в точке с координатами (ω = ωС = 1/T; A(ω)= K)
Первая полупрямая, которая задана в диапазоне 0 < ω < 1/T имеет единичный положительный наклон, а вторая, заданная при1/T< ω < ∞, идет горизонтально.
Логарифмическая ФЧХ представлена арктангенсоидой, которая при
ω = 1/T имеет φ(ω) = п/4, при ω - 0 φ(ω)= +π/2 и приω -∞ φ(ω) стремится к 0
Уравнение переходной функции:
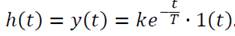
При подаче скачкообразного единичного сигнала на вход звена его выходная переменная скачкообразно увеличивается до y(0)= k 1(t), а затем спадает до нуля по экспоненте с постоянной времени T
Реализация реального дифференцирующего звена
Пример RC-цепочка. Рассмотрим уравнения, передаточную функцию, аппроксимированные ЛАЧХ и переходную функцию электрической цепи
из последовательно включенных конденсатора С и резистора R, в которой
выходное напряжение UВЫХ снимается с резистора R
Уравнение RC -цепочки в операторной форме:
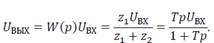
Здесь 
– передаточная функция и постоянная времениRC -цепочки; 
– комплексные величины сопротивлений резистора R и конденсатора C.
При малых частотах, когда ω < 1/T, ёмкостное сопротивление конденсатора больше активного сопротивления резистора. Ток в цепи определяется величиной сопротивления конденсатора, которое по мере роста частоты снижается. Это вызывает увеличение тока и, следовательно, падение напряжения на активном сопротивлении, чему соответствует возрастающий участок ЛАЧХ при малых частотах.
При высоких частотах, когда ω > 1/T, наблюдается |xС| < R, ток в RC -цепи
определяется, главным образом, величиной R, которая от частоты не зависит. По этой причине почти постоянно и падения напряжения на резисторе,в итоге UВЫХ = UВХ = const (горизонтальный участок ЛАЧХ при высоких частотах).
При подаче скачка UВХ конденсатор в первый момент времени ведет себя,как закоротка, следовательно, на переходной функции в момент времени наблюдается скачок выходного напряжения UВЫХ = UВХ. По мере заряда конденсатора и увеличения напряжения на нем ток заряда снижается до нуля.
Вопросы самоконтроля:
1. Представьте реализацию дифференцирующего звена.
2. Охарактеризуйте дифференцирующее звено.
3. Перечислите порядок построения АЧХ, ЛАЧХ и переходного процесса дифференцирующего звена
4. Изобразите ЛАЧХ и переходного процесса RC цепочки