Исходные данные
Стороны прямоугольника АBCD (рис. 1.1) являются осями внешних стен сооружения: AB=CD=8 м. BC=DA=4 м. Точки 1 и 2 – пункты съёмочного обоснования или опорные точки: расстояние между ними 20 м. Индивидуальные исходные данные для расчёта выбирают из таблицы 1.1 по предпоследней цифре k1 и из таблицы 1.2 по последней цифре k2 кода студента.
Таблица 1.1 - Координаты опорных пунктов
| k1 | Координаты пункта 1, м | Координаты пункта 2, м | ||
| x | y | x | y | |
| 73,32 | 34,18 | 88,64 | 47,04 | |
| 73,68 | 34,03 | 88,56 | 47,42 | |
| 74,05 | 33,90 | 88,44 | 47,79 | |
| 74,42 | 33,77 | 88,31 | 48,16 | |
| 74,79 | 33,66 | 88,18 | 48,53 | |
| 75,17 | 33,57 | 88,03 | 48,89 | |
| 75,55 | 33,48 | 87,87 | 49,24 | |
| 75,94 | 33,41 | 87,69 | 49,59 | |
| 76,32 | 33,35 | 87,51 | 49,93 | |
| 9* | 76,71 | 33,31 | 87,31 | 50,27 |
Таблица 1.2 - Размещение сооружения
| k2 | Координаты точки А, м | Дирекционный угол линии АВ | |
| x | y | ||
| 75,99 | 40,34 | 40°00¢ | |
| 76,14 | 40,28 | 42 00 | |
| 76,28 | 40,22 | 44 00 | |
| 76,43 | 40,17 | 46 00 | |
| 76,58 | 40,13 | 48 00 | |
| 76,73 | 40,09 | 50 00 | |
| 76,88 | 40,06 | 52 00 | |
| 77,04 | 40,03 | 54 00 | |
| 77,19 | 40,01 | 56 00 | |
| 77,35 | 39,99 | 58 00 | |
| * | 77,51 | 39,97 | 60 00 |
Порядок выполнения работы
1.2.1 Расчёт координат точек В, С иD
По координатам xA, yA точки А, дирекционному углу aАВ линии АВ и её длине dAB вычисляют координаты точки В по формулам прямой геодезической задачи
. (1.1)
Для функций синуса и косинуса берут не менее 4-х цифр после запятой.
Затем находят дирекционный угол следующей стороны ВС
, (1.2)
и аналогично вычисляют координаты точки С. Координаты точки Dнаходят по дирекционному углу
. (1.3)
Для контроля таким же образом вычисляют координаты точки А от точки D. Вычисленные координаты должны совпасть с исходными координатами точки А. Допустимое расхождение 0,01 м.
После окончания расчёта составляют таблицу координат точек (табл. 1.3) и на отдельном листе отчёта план в масштабе 1:100, построенный по этим координатам (рис. 1.2).
|
|
Делают контрольные измерения на плане: размер прямоугольника должен быть 4´8 см, а длина линии 1-2 (от пункта 1 до пункта 2) 20 см. Следует учесть, что на рисунке 1.2 масштаб плана в 2 раза мельче требуемого.
1.2.2 Подготовка исходных 
данных для выноса точек
Вданном задании требуется рассчитать исходные данные для разбивки четырёх точек сооружения. Для каждой точки предусмотрен свой способ разбивки. Распределение способов между точками А, В, С и D зависит от соотношения цифр k1 и k2 кода студента (табл. 1.4).
Таблица 1.4 - Способы разбивки точек А, В, С и D
| Способ выноса точки | Обозначения точек и пунктов обоснования | |
| 1-й вариант: k1 £ k2 | 2-й вариант: k1 > k2 | |
| Прямоугольных координат | т. А от п. 1 | т. В от п. 2 |
| Полярный | т. В от п. 2 | т. А от п. 1 |
| Угловой засечки | т. С от п. 1 и 2 | т. Dот п. 1 и 2 |
| Линейной засечки | т. Dот п. 1 и 2 | т. С от п. 1 и 2 |
И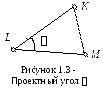 
скомые углы и расстояния вычисляют по координатам точек. Общий принцип вычислений не зависит от способа выноса точек.
Проектный угол b (рис. 1.3) вычисляют через разность дирекционных углов
. (1.4)
При этом, если 
, то 
.
Дирекционные углы вычисляют по формулам
, (1.5)
. (1.6)
Дирекционный угол находят, как правило, в два этапа. Вначале по арктангенсу (1.5, 1.6) вычисляют искомый угол в 1-й четверти (румб), затем в зависимости от знаков приращений Dx и Dy переходят по известным формулам[7] к дирекционному углу.
Расстояние между точками, например LM,вычисляют по одной из трёх формул
|
|
. (1.7)
При использовании калькулятора применяют обычно 1-ю формулу, а 2-ю или 3-ю формулы применяют для контроля.
Контролируют также вычисления дирекционного угла по формуле
. (1.8)
Для этого предварительно вычисляют длины всех сторон треугольника KLM. Последнюю формулу (1.8) применяют только для контроля, потому что функция арккосинуса может дать значительные ошибки в угле, если он близок к 0°или 180°.
При подготовке данных вычисляют по 2 разбивочных элемента.
· В способе прямоугольных координат (рис. 1.4) для точки А (1-й вариант по таблице 1.4) вычисляют 2 координаты: X1 =1Q (длина отрезка от п. 1 до т.Q) и Y =QA, ТочкаQ– основание перпендикуляра, опущенного с т. А на линию 1-2.
Вначале вычисляют вспомогательные величины: угол
и расстояние d1A=1A.
Затем находят искомые величины
.
Индекс 1 при X1 означает, что вычисляется расстояние от точки Q до пункта 1, а не пункта 2.
· В полярном способе для точки В находят угол (рис. 1.5) 
и расстояние 
d2B =2B.
· В угловой засечке для точки С находят два угла (рис. 1.6)
· В линейной засечке для точки Dнаходят два расстояния (рис.1.7)
d1D =1D, d2D =2D.
Угловые разбивочные элементы вычисляют в градусах и минутах с точностью до 1¢, а линейные – в метрах с точностью до 0,01 м. Промежуточные угловые величины – дирекционные углы – можно вычислять в градусах и долях градуса с точностью до 0, 01°. В функции арктангенса следует оставлять не менее 4-х значащих цифр.
Для контроля все 8 разбивочных элементов измеряют с помощью линейки и транспортира на составленном плане и сравнивают с вычисленными элементами. Если расхождения превышают графическую точность (5-10 см для расстояний и 0,5-1°для углов) вычисления и измерения проверяют и исправляют. Следует также проверять по плану и вычисленные дирекционные углы. При этом учитывают, что a21 = a12 +180°.
|
|
Для каждого способа (точки) составляют разбивочный чертёж (рис. 1.4-1.7) с указанием величин разбивочных элементов. Чертежи составляют схематически, не выдерживая точных углов и расстояний. Составляют также таблицу разбивочных элементов (табл.1.5).
Пример вычислений
Исходные данные для примера возьмём из таблиц 1.1 и 1.2 в строках, помеченных знаком *. Все линейные элементы в примере имеют размерность метры. Вначале находим координаты углов сооружения.
· Координаты точки В:
.
· Координаты точки С:
.
· Координаты точки D:
.
· Координаты точки А (контроль):
.
После составления таблицы и плана найдём разбивочные элементы. Возьмём для примера 2-й вариант по таблице 1.4.
· Способ прямоугольных координат для точки В:
Вспомогательные величины:
Разбивочные элементы:
.
· Полярный способ для точки А:
· Угловая засечка для точки D:
· Линейная засечка для точки С:
Отчёт по работе
Студент составляет отчёт, в котором приводит исходные данные, выбранные по коду, результаты всех вычислений, таблицу координат всех пунктов, план, составленный по этим координатам, четыре разбивочных чертежа и таблицу разбивочных элементов.
Таблица 1.5 - Таблица разбивочных элементов
| Выносимая точка | Способ | Разбивочные элементы |
| А | полярный | b 1 =25°09¢; d1 =6,71 м |
| В | прямоугольных координат | X1 =5,93м; Y =3,17 м |
| С | линейной засечки | d1 =15,65 м; d2 =9,36 м |
| D | угловой засечки | b 1 =49°04¢; b2 =25°57¢ |
Домашнее задание: изучить материал выполненной практической работы, законспектируйте порядок её выполнения.
Выполненную работу отправьте по email lenka_33_74@mail.ru в виде фото конспекта лекции.
Не забудьте указать свои Фамилию Имя и группу!
Обратите внимание на правила оформления работы, указания приведены в сообществе https://vk.com/club194232314