Фильтр Калмана
Фильтр Калмана это эффективный рекурсивный фильтр, который оценивает состояние линейной динамической системы по серии неточных измерений. Он используется в широком спектре задач от радаров до систем технического зрения, и является важной частью теории управления системами.
Калман в своих работах модифицировал постановку задачи многомерной фильтрации Винера, придав ей форму проблемы пространства состояния. В результате такой модификации был получен фильтр Калмана, осуществляющий процедуру рекурсивного оценивания, когда подлежащий оцениванию сигнал является входным сигналом линейной нестационарной динамической системы.
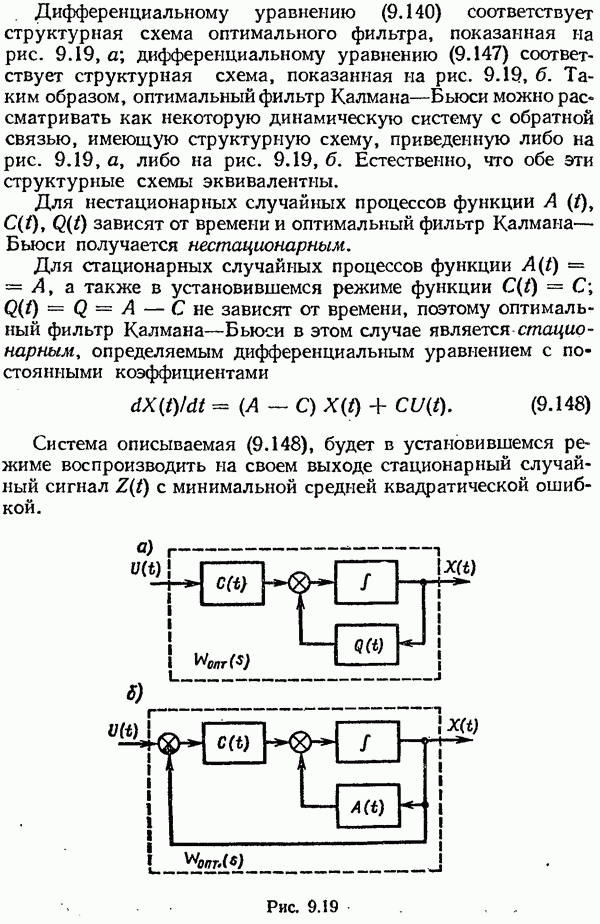
Синтез наблюдателя Калмана для оптимальных САУ
Рассмотрим непрерывную модель объекта управления
(5.1.11)
с известными входами u и возмущениями по входам w и измерениям n, которые являются "белым" шумом со следующими характеристиками:
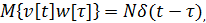(5.1.12)
Требуется выполнить синтез наблюдателя для оценивания вектора переменных состояния объекта, который минимизирует установившуюся ошибку оценивания
(5.1.13)
Оптимальным решением является фильтр Калмана, описываемый уравнениями
(5.1.14)
где матрица коэффициентов обратных связей L определяется на основе решения алгебраического матричного уравнения Риккати. Например, при Н=0 дисперсия P определяется из уравнения
AP + PAT – (PCT +GN)R-1(CP+NTGT) + GQGT = 0, (5.1.15)
матрица L:
L = APCT(N+CPCT)-1. (5.1.16)
Наблюдатель (рис. 3) объединяет фильтр Калмана и объект управления.
Рисунок 5.1.1 –– Наблюдатель Калмана
Наблюдатель использует известные входы u и результаты измерений yv, искаженные случайными помехами, для того, чтобы вычислить оценки вектора переменных состояния 
и выходов 
.
Пусть задана дискретная модель объекта управления
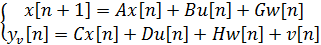(5.1.17)
с известными входами u и возмущениями по входам w и измерениям v, которые являются "белым" шумом со следующими характеристиками:
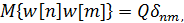
(5.1.18)
Требуется выполнить синтез наблюдателя для оценивания вектора переменных состояния объекта управления, который минимизирует установившуюся ошибку оценивания,
. (5.1.19)
В этом случае фильтр Калмана описывается уравнениями:
, (5.1.20)
где матрица коэффициентов обратных связей L и новая матрица коэффициентов обратных связей М определяются на основе решения матричного алгебраического уравнения Риккати.
Наблюдатель объединяет фильтр Калмана и объект управления; он использует известные входы u[n] и результаты измерений уv[n], искаженные случайными помехами, для того, чтобы вычислить оценки вектора переменных состояниях[n] и выходов у[n].
Обновленная матрица коэффициентов обратных связей М применяется для того, чтобы уточнить предсказание х[n] на основе измерения уv [n]
. (5.1.21)
Для синтеза фильтра Калмана в предназначены следующие функции Control System Toolbox:
[kest, L, P] = kalman(sys, Qn, Rn, Nn)
[kest, L, P] = kalman(sys, Qn, Rn, Nn, sensors, known)
для дискретных моделей
[kest, L, P, M, Z] = kalman(sys, Qn, Rn, Nn)
для синтеза дискретного фильтра Калмана для непрерывных систем
[kest, L, P, M, Z] = kalmz(sys, Qn, Rn, Nn)
Приведенные выше функции выполняют синтез фильтров Калмана для оценки переменных состояния объекта управления на основе данных о случайных внешних возмущениях и ошибках измерений.
На систему, описывающую объект управления и случайные воздействия накладываются следующие ограничения:
1. пара матриц (С, A) должна быть обнаруживаемой;
2. необходимо выполнение неравенств
, (5.1.22)
с учетом обозначений
. (5.1.23)