Примеры решения задач, решаемых методом ГМТ

Задача 1. На стороне треугольника найти точку, равноотстоящую от двух

других сторон треугольника.

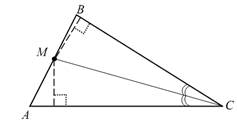
Анализ. Пусть задача решена и точка М на стороне АВ находится на

одинаковом расстоянии от сторон АС и ВС, образующих угол С.

Так как все точки, равноудаленные от сторон угла С лежат на биссектрисе этого угла (гмт 5), то точка М удовлетворяет двум независимым условиям:

Построение:

 

Доказательство. Легко видеть, что точка М удовлетворяет требованиям

задачи.

 

Задача 2. Построить треугольник по основанию а, углу при вершине А

медиане m_а.

Анализ. Допустим, что задача решена и искомый треугольник ΔАВС

построен так, что BC = a, AM = m_а – медиана и ∟ВАС = α.

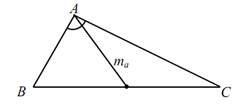Отрезок ВС, равный данному, всегда может быть построен. Тогда задача сводится к построению точки А, удовлетворяющей двум независимым условиям:

1⁰. Точка А находится на расстоянии m_а от середины М стороны ВС, т.е.

2⁰. Так как ∟ВАС = α, то точка А принадлежит ГМТ F1, из которых отрезок ВС виден под углом α, т.е.

Таким образом,

Заданные по условию задачи элементы могут быть выбраны перед построением или анализом.

Построение:

 

Доказательство: BC = a, AM = m_а по построению, и ∟СВО = 90⁰ – α, следовательно, ∟ВОМ = α, следовательно, ∟ВОС=2α, а ∟ВАС =0,5*∟ВОС= α

и, следовательно ΔАВС, удовлетворяет всем условиям задачи и потому искомый.

Исследование: Задача имеет столько решений, сколько точек содержит

пересечение двух окружностей. Если пересечение в двух точках, то два

решения; в одной (окружности касаются) – одно решение, не пересекаются –нет решений.

 

Задача 3. Построить окружность данного радиуса r, проходящую через данную точку М и высекающую на данной прямой l отрезок длины d, равный данному.

Анализ: Пусть искомая окружность построена. Пусть О – ее центр, r – данный радиус, М – данная точка, АВ – хорда длины d, построенной окружности, лежащей на данной прямой l. Опустим перпендикуляр ОC на прямую l. В прямоугольном треугольнике ОВС известна гипотенуза (данный радиус r) и катет ВС, равный половине данного отрезка. Кроме того, ОМ = r.

Значит, искомый центр О принадлежит, во-первых ГМТ F1, удаленных от данной прямой l на расстояние, равное ОС(ГМТ 3); во-вторых ГМТ F2, удаленных от данной точки М на расстояние, равное данному радиусу r (гмт2).

Окружность ω может быть построена, ГМТ F1 может быть построено, если мы найдем расстояние OC = h.

Для этого построим вспомогательный треугольник О₁В₁С₁ по гипотенузе О₁В₁ = r и катету В₁С₁ = d/2. Тогда h = O₁C₁ будет найден.

Построение:

 

Доказательство: Убеждаемся в том, что построенная окружность удовлетворяет всем требованиям задачи. OM = r по построению. Докажем, что AB = d.

Действительно, ΔАОВ - равнобедренный (ОС –

медиана и высота), отсюда АВ = 2ВС = 2*d/2 = d.

Исследование: Построение 1 возможно, если d < 2r. Построения 2 - 3 выполняются и притом однозначно. Построение 4 возможно лишь тогда, когда прямая F1 и окружность F2 пересекаются, то есть при условии, что расстояние от точки М до прямой l не больше, чем При этом прямая F1 пересекает окружность в двух или одной точке соответственно. Таким образом, задача может иметь одно, два или не иметь решений.

 

Задача 4. Построить треугольник АВС, зная угол А, основание а и радиус r вписанной окружности.

Анализ. Пусть искомый треугольник построен и пусть ВС = а, ∟ВАС = ∟А, О - центр вписанной окружности и OK = r. Легко видеть, что построив ВС = а и центр вписанной окружности, мы смогли бы построить и вершину А, и треугольник АВС будет построен. Отрезок ВС = а мы всегда можем построить (Построение 1). Тогда задача сводится к построению точки О. Одно свойство (условие 1⁰) точки О можно отметить сразу – она находится на расстоянии r от стороны ВС, то есть центр О вписанной окружности принадлежит ГМТ, находящихся на расстоянии r от прямой ВС (ГМТ 3). (Как правило, мы строим только в одной из двух полуплоскостей, определяемых заданной прямой). Второе свойство, которым обладает точка О, видно не сразу. Но, исходя из свойств вписанной окружности, это свойство мы можем найти: центр вписанной окружности находится на пересечении биссектрис треугольника и потому ОВ и ОС – биссектрисы углов В и С.

Тогда: ∟ВОС = 180⁰ – 0,5(∟В + ∟С) = 180⁰ – 0,5 (180⁰ - ∟А) = 90⁰ + 0,5∟А

Так как ∟ВОС =90⁰ +∟A/2, то точка О принадлежит ГМТ F2, из которых

данный отрезок ВС виден под данным углом α = 90⁰ + ∟А/2 (ГМТ 6). ГМТ F1 и F2 может быть построено, а потому и точка может быть построена и мы можем перейти к построению искомой фигуры.

Построение:

 

 

 

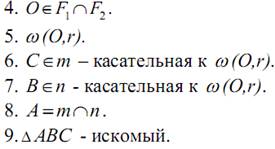
Доказательство: Убеждаемся в том, что построенный треугольник

удовлетворяет всем требованиям задачи. ВС = а, окружность ω(O,r) вписана в

треугольник по построению. Остается доказать, что ∟ВАС равен данному углу

А. Действительно, по построению ∟О₁ ВК = ∟А/2. Тогда

Теперь находим:

Значит, ΔАВС удовлетворяет всем условиям задачи, а потому – искомый.

Исследование. Построения 1-3 выполняются и притом однозначно при

любых a, r и ∟ A<180⁰. Построение 4 возможно лишь тогда, когда прямая F1

пересекает окружность F2, то есть при условии или при: (*). При этом прямая F1 пересекает окружность F2 в

двух или одной точке соответственно. Построения 6 и 7 всегда выполнимы, так

как из любой точки вне окружности можно провести к ней две касательные

(одна из них в данном случае прямая ВС). А вот построение 8 возможно не всегда: прямые m и n могут быть параллельными или могут пересекаться в полуплоскости, не содержащей точку О. В этих случаях в нужной нам полуплоскости точка А не строится. Вывод: при выполнении условий ∟A<180⁰ и (*) задача может иметь одно, два или ни одного решения.

 

4. Построение Штейнера и построение с помощью
двусторонней линейки, прямого или острого угла [2], [5]

Якоб Штейнер (18.05 1795г. – 01.04.1863г.) сын простых поселян из Уцисдорфа Германии. Как он сам писал: «Только на девятнадцатом году стремление к образованию стало для меня потребностью…. и с осени 1822г. Вынужден с величайшим трудом добывать средства к существованию частными уроками. Почти бессознательно я пришел таким образом к собственно геометрическому способу рассмотренья, как оно должно быть присуще геметрии древности, но я находился в случае, противоположном им. Мне было дано множество разрешимых задач и предложений, и мне приходилось заняться не фиксацией отдельных предложений, а установлением того свойства общих законов систематического построения, что из них вытекают все открытия подобного рода, и их соответственным образом исчерпать».

«Геометрия в более тесном смысле для своих построений нуждается только в двух инструментах, циркуле и линейке. …. все построения могут быть выполнены только при помощи линейки, если где-либо в дан будет вспомогательный неподвижный круг»

Рассмотрим решение задач проведением только одних прямых линий, причём на чертеже иногда уже имеется начерченной какая-нибудь одна вспомогательная фигура. Из всех таких способов наиболее сильными являются решения с помощью:

1. Двусторонней линейки, другие инструменты при этом не допускаются

2. Прямого или острого угла, сделанного из дерева или металла - другие инструменты не допускаются.

3. Односторонней линейки, причём на чертеже уже имеется начерченной окружность с известным центром.

Далее, всякая не вспомогательная окружность считается данной, если известно положение ее центра и длина радиуса, заданная где-нибудь начерченным отрезком. Однако ни одна точка такой окружности точку какого-нибудь свойства, то должны ограничиться проведением только прямых линий.

Мы знаем, что решение квадратной задачи сводится к известным четырём основным построениям.

Из этих основных задач первая и третья решаются способами 1, 2 и 3

непосредственно — одной линейкой. Моя цель показать, что две другие основные задачи решаются теми же тремя способами, которые решают теми же способами всякую квадратную задачу.

Решим несколько задач проведением одних прямых линий (односторонней линейкой).

 

Задача №1.

Найти геометрическое место центров окружностей, проходящих через две данные точки.

 

 

 

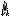
Решение:

Пусть окружность с центром O проходит через данные точки A и B. Поскольку OA = OB (как радиусы одной окружности), точка O лежит на серединном перпендикуляре к отрезку AB. Обратно, каждая точка O, лежащая на серединном перпендикуляре к AB, равноудалена от точек A и B. Значит, точка O — центр окружности, проходящей через точки A и B.

Построение:

Проведем диаметры АА1, ВВ1, затем хорды АВ1, ВА1, эти последние перпендикулярны АВ и потому параллельны между собой. Поэтому для решения задачи нужно провести через точку О прямую, параллельную эти хордам. Она будет серединным перпендикуляром к АВ, т.е. искомым ГМТ [5, стр.21]

 

Задача №2.

Дан прямоугольник ABCD. Найдите ГМТ X, для которых AX + BX = CX + DX.

 

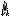
Решение:

Пусть l — прямая, проходящая через середины сторон BC и AD.

Предположим, что точка X не лежит на прямой l, например, что точки A и X лежат по одну сторону от прямой l. Тогда AX < DX и BX < CX, а значит, AX + BX < CX + DX. Поэтому прямая l — искомое ГМТ.

Построение:

Проведем диагонали АD и ВС. Из точки Е (точка пересечения диагоналей) проведем прямую, параллельную сторонам AD или CD. Так как диагонали в точке Е делятся пополам, то и стороны AC и BD будут делиться пополам, следовательно построенная прямая – искомое ГМТ.

(Можно воспользоваться способом деления сторон AC и BD пополам [5, стр.22].

 

 

Задача №3. На данной прямой найдите точку одинаково удаленную от двух заданных точек.

 

 

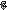
Решение:

Пусть c – данная прямая, A, B – данные точки. Геометрическим местом точек, одинаково удаленных от точек A и B, является серединный перпендикуляр к отрезку AB. Если серединный перпендикуляр и прямая c пересекаются, то искомой точкой C будет их точка пересечения. Если они не пересекаются, то задача не имеет решения.

Построение:

Из произвольной точки С прямой с проведем прямую 1, параллельную отрезку АВ. От точки С отложим два одинаковых отрезка в обе стороны от точки С (СК и СМ). Проведем прямые АК и ВМ до пересечения в точке О. Тогда прямая ОС делит отрезок АВ пополам.

Другую произвольную точку С1 на прямой 1 соединим с точками А и В. Прямые С1В и АС пересекутся в точке О1. Прямая ОО1 и будет срединным перпендикуляром. Пересечение ОО1 с прямой с даст искомую точку.

 

 

Задача №4.

Найти точки, одинаково удаленные от прямых, на которых лежат стороны данного треугольника.

 

 

 

 

Решение:

Рассмотрим треугольник ABC. Точка D этого треугольника одинаково удалена от AB и AC, если она принадлежит биссектрисе угла A. Аналогично, точка D треугольника ABC одинаково удалена от AB и BC, если она принадлежит биссектрисе угла B. Таким образом, точкой одинаково удаленной от AB, AC и BC будет точка пересечения биссектрис углов A и B треугольника ABC.

Построение:

Для построения биссектрисы угла А из произвольной точки А1 на стороне АВ, проведем прямую, параллельную стороне АС, и соответственно из точки А2 на стороне АС, прямую, параллельную АВ. Точку пересечения прямых соединим с вершиной А. Полученная прямая есть биссектриса угла А. Аналогично строим биссектрису угла В.

 

 

Задача №5.

Построить треугольник по a, b и углу В= при основании.

 

 

 

Решение: Предположим, что задача решена и треугольник АВС – искомый. Построить этот треугольник можно, если знать, например, положение всех его вершин. Положение вершин В и С можно считать известным, тогда остается найти точку А. А – искомая точка. Чтобы найти искомое, надо знать его геометрические вытекающие из условия задачи свойства. Первое свойство точки А: она является вершиной треугольника с основанием ВС=а и данным углом АВС при основании. Следовательно, точка А принадлежит ГМТ 4, т. е. лучу ВА (составляющему с основанием ВС угол b) или лучу ВА, являющемуся образом ВА при симметрии относительно ВС. Однако положение точки А на плоскости (относительно точек В и С) по одному этому свойству найти не удастся. Выясним второе свойство точки А. Оно очевидно: точка А удалена от точки С на данное расстояние b, т. е. А принадлежит ГМТ 1 – окружности (С,b).

Построение:

Проведем отрезок ВС=а. В точке В необходимо построить угол, равный [5, стр. 59].

Наташа. Перерисуй и перепиши решение из книги, да и остальные рисунки. Я та Visio и не скачал.

 

Заключение.

Окружающий нас мир – это мир геометрии

А. Д. Александров

Вокруг нас находится большое количество предметов, имеющих форму геометрических фигур. Углы, отрезки и плоскости являются объектами искусственного происхождения и изготовлены человеком. Предметы природного происхождения имеют округлые формы, такие как шар, окружность, дуга.

Гражданское строительство и архитектура использует этот раздел математики для возведения различных объектов.

Геометрия, как и остальные разделы математики, зародилась из практических соображений и ее с любовью развивали, чтобы изучать формы. Геометрия связана с такими науками, как физика, биология, астрономия. Сегодня она имеет огромное количество практических применений. Кроме того, она необходима для описания Вселенной.

В своей работе мы исследовали различные задачи и методы построения с помощью циркуля и линейки, в том числе на геометрическое место точек, построения Штейнера. Рассмотрены задачи и даны их решения.

Здесь нами было использовано практически все четыре этапа: анализ, построение, доказательство и исследование.

Моя работа выполнена с помощью учителя, так как встречаются задачи, которые я не могла бы решить сама. Но в принципе моя работа направлена на то, чтобы показать красоту геометрии и возможность выполнять красивые работы с помощью геометрических фигур.

Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ.

Литература:

1. История математики с древнейших времен до начала XIXстолетия (в трех томах) под ред. А.П. Юшкевича, Т.1 «С древнейших времен до начала нового времени», Издательство «Наука», Москва, 1970г., 353 стр.

2. И.И. Александров. Сборник геометрических задач на построение, Учпедгиз, 1950г., 177стр.

3. Б.И. Аргунов, М.Б. Балк. Геометрические построения на плоскости. Москва., Учпедгиз 1957г., 268стр.

4. Атанасян Л.С. и др. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – Москва: «Просвещение». 1998.

5. Я. Штейнер. Геометрические построения, выполняемые с помощью прямой линейки и неподвижного круга. М. 1939г. 81стр.