Исследование частотных характеристик цифровых фильтров
Уфа 2006
Лабораторная работа №1
Исследование частотных характеристик
цифровых фильтров
Цель работы: освоение методов нахождения АЧХ цифровых ФНЧ
Частотные характеристики ЦФ
Пусть:
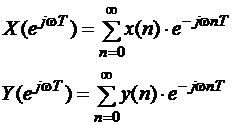
Тогда ЧХ – частотная характеристика
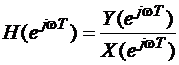
При  ПФ
ПФ 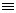 ЧХ
ЧХ
ЧХ – комплексная величина
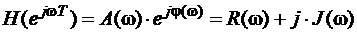
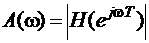 - АЧХ
- АЧХ
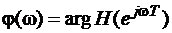 - ФЧХ
- ФЧХ
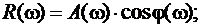
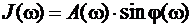 .
.
Групповое время задержки (групповое время замедления) ГВЗ
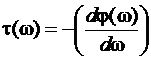
Физический смысл ГВЗ – это мера средней задержки, вносимой фильтром в зависимости от частоты.
Основные свойства ЧХ:
1. Все ЧХ – непрерывные функции частоты.
2. Все ЧХ – периодические функции частоты, с периодом равным 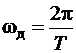
3. Для фильтров, ПФ которых имеют только вещественные коэффициенты: 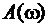 и
и 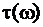 - чётные функции частоты
- чётные функции частоты
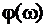 - нечётные функции
- нечётные функции
Из 2 и 3 следовательно требования к ЧХ фильтров с вещественными коэффициентами достаточно задавать на интервале от 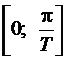
Пример 1:
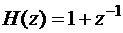 ;
;
Найти: АЧХ, ФЧХ, ГВЗ.

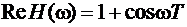
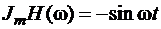

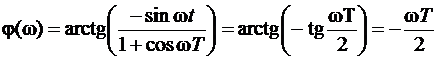
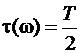
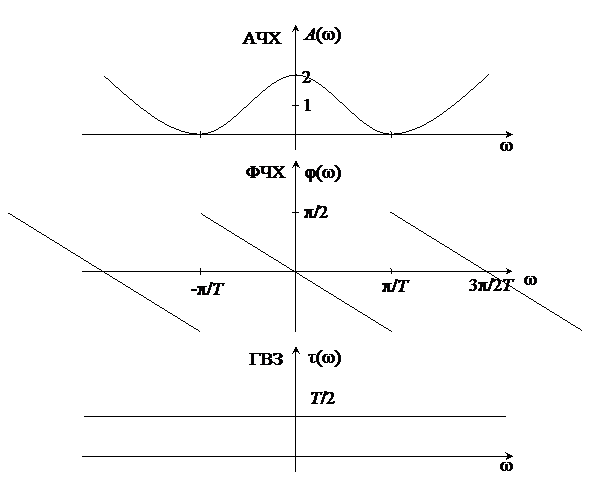
Рис. 10
Пример 2:

Найти ФЧХ и ГВЗ.
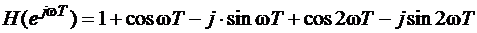
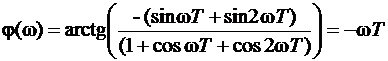
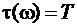
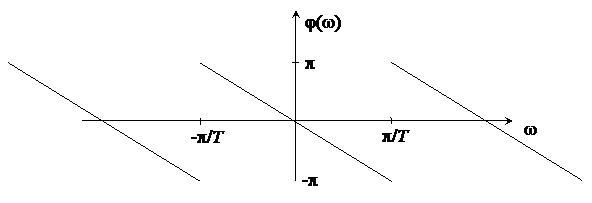
Рис. 11
Нормирование частоты
Для того чтобы частотные характеристики разных фильтров легче было сравнивать друг с другом, частоту нормируют.
Т.к. все частотные характеристики зависят при постоянном периоде от произведения  , вместо
, вместо  вводят одну переменную.
вводят одну переменную.
Как правило используют два способа нормирования частоты:
1) 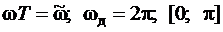 - требования к ЧХ на этом интервале.
- требования к ЧХ на этом интервале.
2)
а) 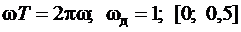
| - Гольденберг |
б) 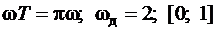
| - MATLAB |
Формулировка требований
к частотным характеристикам фильтра
Избирательный фильтр служит для выделения частотных составляющих входного сигнала, расположенных в полосе пропускания фильера, и подавления частотных составляющих, расположенных в полосе задерживания. В зависимости от того, каким образом указанные полосы расположены относительно друг друга на частотной оси, различают следующие типы фильтров: нижних частот (ФНЧ), верхних частот (ФВЧ), полосовые (ПФ) и режекторные (РФ). На рис.1 приведены идеализированные амплитудно-частотные характеристики соответствующих фильтров.

Рис.1
Естественно, что фильтры с такими характеристиками построить невозможно, к идеализированным характеристикам можно только приблизиться. На этапе решения аппроксимационной задачи определяют передаточную функцию H (z) фильтра, которая воспроизводила бы заданную АЧХ A (w) с требуемой точностью. Отсюда следует, что в качестве исходных данных для решения аппроксимационной задачи должны быть заданы допуски на максимальное значение неравномерности АЧХ в полосе пропускания (D А п) и максимальное отклонение АЧХ от нуля в полосе задерживания (D А з).
Требования к фазочастотной характеристике фильтра при проектировании избирательных БИХ-фильтров описанными ниже методами не могут быть заданы, ФЧХ получается нелинейной. Степень нелинейности ФЧХ можно лишь проконтролировать путем расчета фазочастотной характеристики или группового времени замедления для определенной (рассчитанной) передаточной функции БИХ-фильтра. Методы построения БИХ-фильтров с заданными требованиями как к АЧХ, так и к ФЧХ достаточно сложны, базируются, как правило, на использовании дополнительного корректора ФЧХ и здесь не рассматриваются.
Таким образом, исходными данными для решения аппроксимационной задачи являются граничные частоты полос пропускания и задерживания, а также величины D А п и D А з.
Пример 1. Разрабатывается цифровой фильтр нижних частот с полосой пропускания от 0 до 0,2 (частота нормирована) и полосой задерживания от 0,4 до 0,5. Частотные составляющие входного сигнала в полосе пропускания должны быть ослаблены не более чем в  раза, а в полосе задерживания подавлены не менее чем в 100 раз. Необходимо задать требования к АЧХ фильтра.
раза, а в полосе задерживания подавлены не менее чем в 100 раз. Необходимо задать требования к АЧХ фильтра.
Соответствующие требования показаны на рис. 2,а, где нормированная граничная частота полосы пропускания w г.п=0,2, нормированная граничная не требования к АЧХ частоты полосы задерживания w г.з=0,4, D А п=1-  = 0,293, D А з=0.01. Обратите внимание, что между полосой пропускания и полосой задерживания существует переходная полоса, для которой требования к АЧХ, как правило, не задаются.
= 0,293, D А з=0.01. Обратите внимание, что между полосой пропускания и полосой задерживания существует переходная полоса, для которой требования к АЧХ, как правило, не задаются.
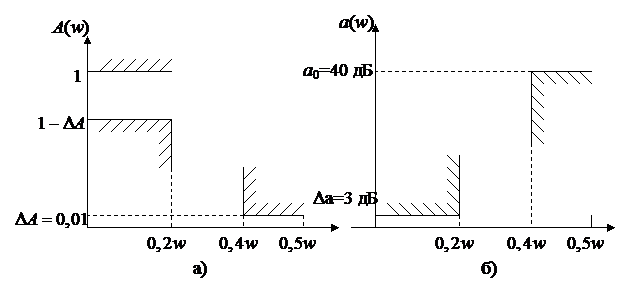
Рис.2
В качестве исходных данных при решении аппроксимационной задачи часто задаются A (w), а требования к характеристике затухания a (w). Эти характеристики связаны между собой простым соотношением
a (w)=-20lg A (w). (1)
 При этом в качестве исходных данных должны быть заданы верхняя граница рабочего затухания в полосе пропускания D а и нижняя граница затухания в полосе задерживания а 0.
При этом в качестве исходных данных должны быть заданы верхняя граница рабочего затухания в полосе пропускания D а и нижняя граница затухания в полосе задерживания а 0.
Связь между параметрами D А п и D а, а также D А з и а 0 можно установить, используя (1):
D а = - 20lg (1-D А п);
а 0 = -20lg(D А з).
Следует заметить, что амплитудно-частотная характеристика A (w) не имеет размерности, а характеристика затухания a (w) определена в децибелах.
Пример 2. Необходимо задать требования к характеристике затухания a (w) для ФНЧ, аналогично рассмотренному в примере 1. Соответствующие требования показаны на рис. 2,б. Действительно, используя (1), получаем D а = - 20lg (1-0,293) = 3 дБ, а 0 = -20lg 0,01 = 40 дБ.
Схемы допусков на амплитудно-частотную характеристику A (w) и характеристику затухания a (w) приведены на рис. 3 и 4 соответственно для фильтров нижних частот (а), верхних частот (б), полосовых (в) и режекторных (г).

Рис.3 Рис.4
В заключение надо отметить, что указанные параметры (граничные частоты и D А п(D а), D А з (а 0)) являются основными при постановке аппроксимационной задачи и часто дополняются некоторыми более частными требованиями. Например, в ряде случаев требуется обеспечить монотонность АЧХ (затухания) в полосе пропускания. Могут также задаваться требования к допустимому отклонению фазочастотной характеристики от заданной (например, линейной). Наконец, могут задаваться требования и к реализационным параметрам разрабатываемого фильтра. Все эти требования так или иначе влияют на формулировку и решение аппроксимационной задачи. Мы, однако, вначале будем рассматривать методику решения аппроксимационной задачи в наиболее простом виде – при задании в качестве исходных данных только основных параметров (w г.п ,w г.з, D А п(D а) и D А з (а 0)).
КРАТКИЙ ОБЗОР МЕТОДОВ РЕШЕНИЯ АППРОКСИМАЦИОННОЙ ЗАДАЧИ.
При определении передаточных функций БИХ-фильтров используется три класса методов:
- методы преобразования аналоговых фильтров в цифровые;
- прямые методы расчета БИХ-фильтров;
- методы, использующие алгоритмы оптимизации.
Для расчета избирательных БИХ-фильтров со стандартными характеристиками (ФНЧ, ФВЧ, ПФ, РФ) наиболее простым и широко используемым является метод билинейного преобразования. С помощью этого метода передаточная функция T (s) аналогового фильтра-прототипа преобразуется в передаточную функцию H (z) цифрового БИХ-фильтра. Достоинством метода билинейного преобразования является то, что передаточная функция цифрового фильтра определяется с помощью простых формул из передаточной функции аналогового фильтра, для которых существуют подробные таблицы и справочники. Это, в свою очередь, позволяет решать аппроксимационную задачу даже в достаточно сложных случаях без использования ЭВМ.
Достоинством метода билинейного преобразования по сравнению с другими методами преобразования аналоговых фильтров в цифровые (инвариантности импульсной характеристики и согласованного z -преобразования) является то, что данный метод обеспечивает построение такого БИХ-фильтра, выходной сигнал которого приближенно совпадает с выходным сигналом аналогового фильтра-прототипа при одинаковых произвольных входных сигналах.
БИЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ.
Билинейное преобразование представляет собой конформное отображение точек s-плоскости в точки z -плоскости и использует замену переменной вида
s = g[(1- z -1)/(1+ z -1)] = g[(z -1)/(z +1)], (3)
где g - постоянный множитель, значение которого не меняет формы преобразования (о выборе величины g поговорим позже). Из (3) можно найти обратное соотношение
z = (g+ s)/(g- s). (4)
Использование подстановки (3) обеспечивает однозначное преобразование передаточной функции T (s) аналогового фильтра-прототипа (АФ-прототипа) в передаточную функцию H (z) цифрового фильтра:
H (z) = T (s)ç 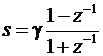
Рассмотрим преобразование (3). Каждой точке комплексной s- плоскости (s= å+ ј Ω) ставится в соответствие определенная точка z -плоскости (z =exp (σ+ ј ω) T).
Мнимая ось s -плоскости (s = ј Ω для -∞< Ω< ∞) отображается в единичную окружность z -плоскости (z =exp(ј ω T)). Действительно, при s = ј Ω из (4) получаем
z =(g+ ј ω)/(g- ј ω).
Представим теперь последнее выражение в показательной форме, т.е выделим модуль r и аргумент θ:
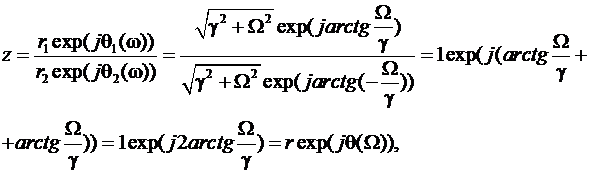 (6)
(6)
Из (6) видно, что r =| z |=1. При монотонном изменении Ω от -∞ до ∞ фазовый угол θ (Ω) монотонно изменяется от -p до p, т.е точка ј Ω1, расположенная на мнимой оси в s -плоскости, отображается в соответствующую точку ехр (ј 2arctg (Ω1/g)).
В частности, для Ω=0 имеем z =exp(ј 0)=1, для Ω=∞ получаем z =exp (ј p)= -1 и для Ω=-∞ имеем z =exp(ј p)=-1.
Левая половина s -плоскости (Re(s) = Re(å+ ј Ω)<0) отображается в часть z -плоскости внутри единичного круга (| z |<1). Действительно, при Re(s)<0 имеем å<0. Тогда из (4) можно получить
z =[(g+å)+ ј Ω]/[(g-å)- ј Ω]. (7)
Теперь поступив точно так же, как при выводе (6), получим
z = r exp(ј θ(Ω)), (8)
где

Поскольку å<0, то модуль числителя в (7) всегда меньше модуля знаменателя, т.е r=| z |<1.
Пример 4. Расположение точек в s -плоскости показано на рис. 7. Определить соответствующие точки z -плоскости (положить g=1), если s 1=-2+ ј 0; s 2=0+ ј 1,0; s 3=0- ј 1,0.

Рис.7
Используя (7), получаем z 1=(1-2)/(1+2)=-0,333, а из (6) имеем z 2=1 exp(ј 2 arctg 1)=exp (ј p/2) и z 3=1 exp (ј 2 arctg (-1))=exp (- ј p/2). Расположение точек в z -плоскости, а также правила отображения мнимой оси и левой половины s -плоскости в единичную окружность и часть z -плоскости внутри единичного круга показаны на рис. 7.
Очень важными являются два обстоятельства. Во-первых, поскольку все полюсы устойчивого аналогового фильтра расположены в левой половине s -плоскости, он при преобразовании к цифровому фильтру будет давать устойчивый фильтр. Во-вторых, так как мнимая ось s -плоскости отображается на единичную окружность z -плоскости, то все максимумы и минимумы АЧХ | Т (ј Ω)| аналогового фильтра сохраняются и в АЧХ | H (e j ω T )| цифрового фильтра. Сохраняется также и неравномерность АЧХ для соответствующих диапазонов частот. Таким образом, избирательные аналоговые фильтры преобразуются в соответствующие цифровые фильтры (например, если аналоговый фильтр есть фильтр нижних частот с неравномерностью АЧХ в полосе пропускания D А п и отклонением АЧХ от нуля в полосе задерживания D А з, то соответствующий цифровой фильтр будет также фильтром нижних частот с параметрами D А з и D А п).
Но не все так хорошо. Так, соотношение между «аналоговыми» частотами Ω и «цифровыми» частотами ω, которое можно получить из (3), является нелинейным:
Ω=g tg (ω T / 2)= g tg (p w), (9)
Где w =ω/ωд нормированная цифровая частота. Таким образом, имеет место деформация шкалы частот при переходе от аналогового фильтра к цифровому. На рис.8 изображена зависимость (9) и проиллюстрировано явление деформации частотной шкалы.

Рис.8
Слева показана идеализированная АЧХ полосового фильтра с двумя полосами пропускания, равными по величине, но расположенными в разных частотных диапазонах. Полученный цифровой фильтр будет иметь также две полосы пропускания, но ширина последней в области верхних частот будет существенно меньше ширины полосы пропускания в области нижних частот.
Выход, однако, чрезвычайно прост. Деформация шкалы частот для частотно-избирательных фильтров (ФНЧ, ФВЧ, ПФ, РФ), аппроксимируемая АЧХ которых имеет вид кусочно-постоянной функции, не приводит к нарушению избирательных свойств фильтра при билинейном преобразовании (и это главное!). А деформацию шкалы частот можно скомпенсировать с помощью предыскажений в аналоговом фильтре.
Рассмотрим, наконец, вопрос о выборе параметра g в подстановке (3). Если использовать соотношение
g=ctg (ωг.п T/ 2)=ctg (p w г.п), (10)
то для получения цифрового фильтра нижних частот с граничной частотой полосы пропускания ωг.п (w г.п) надо в качестве прототипа использовать нормированный аналоговый фильтр с частотой среза Ωс=1, а именно такие фильтры и приводятся в справочниках.
Пример 5. Рассмотрим порядок действий при определении передаточной функции H (z)цифрового ФНЧ по заданным требованиям к неравномерности АЧХ в полосе пропускания D А п, отклонению от нуля в полосе задерживания D А з, а также граничным нормированным частотам полос пропускания w г.п и задерживания w г.з (рис.9).

Рис.9
Вначале определим соответствующие граничные частоты полосы пропускания Ωс и полосы задерживания Ωк аналогового фильтра с помощью нелинейного соотношения (9). Графически этот процесс показан на рис. 9. Теперь надо определить передаточную функцию T (s) аналогового фильтра-прототипа с неравномерностью АЧХ в полосе пропускания [0, Ωс], равной D А п, и отклонением от нуля в полосе задерживания [Ωк,∞], равным D А з. Это можно сделать с помощью справочника по расчету аналоговых фильтров [6]. Работу со справочником мы рассмотрели выше. Доустим, АФ найден и его АЧХ показана на рис. 9. Теперь надо выполнить билинейное преобразование (5), т.е в определенной из справочника передаточной функции T (s) выполнить замену переменной s в соответствии с (3). В результате получим БИХ-фильтр, удовлетворяющий поставленным требованиям.
Билинейное преобразование можно выполнить как вручную (с помощью калькулятора), так и на ЭВМ.
Расчет частотной характеристики
Частотная характеристика дискретного фильтра рассчитывается с помощью функции freqz, которая очень похожа на функцию freqs, выполняющую аналогичные расчеты для аналоговых цепей.
В простейшем виде функция freqz используется следующим образом:
freqz(b, a)
Входные параметры b и а — векторы коэффициентов полиномов числителя и знаменателя функции передачи фильтра.
При расчете используются нормированные значения частот, измеряемые в радианах на отсчет (при такой нормировке частота дискретизации равна 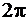 , а частота Найквиста —
, а частота Найквиста —  ). По умолчанию выбирается 512 частотных точек, равномерно распределенных в диапазоне 0...
). По умолчанию выбирается 512 частотных точек, равномерно распределенных в диапазоне 0...  .
.
При отсутствии выходных параметров функция freqs строит графики АЧХ (в децибелах) и ФЧХ (в градусах) фильтра.
Построим графики частотных характеристик фильтра, использованного при демонстрации дискретной свертки, но добавим к этому фильтру рекурсивную ветвь с коэффициентом передачи 0,1. Результат показан на рис. 10:
>> b = [1 2 3 4];
>> a = [1 2 3 4];
>> freqz(b, a)
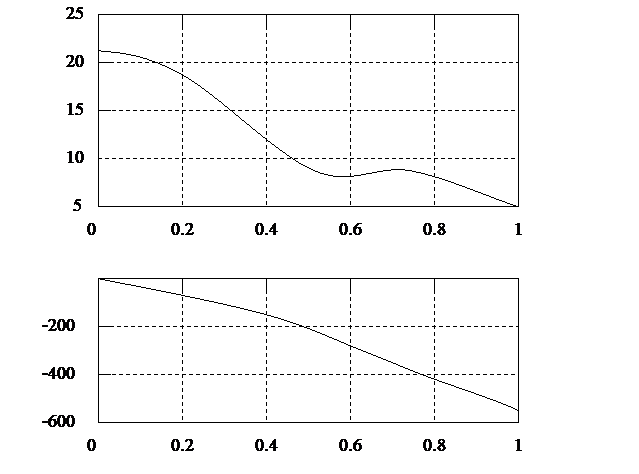
Рис. 10. Частотная характеристика дискретного фильтра, построенная функцией freqz
Если при вызове функции указаны выходные параметры, построение графика не производится:
[h, w] = freqz(b, a);
В векторе h возвращаются рассчитанные значения комплексного коэффициента передачи, а в векторе w – использованные при расчете значения нормированных частот.
Чтобы задать количество частотных точек для расчета, используется третий входной параметр n (частоты при этом по-прежнему равномерно распределяются в диапазоне 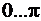 ):
):
freqz(b, a, n);
Можно заставить функцию freqz использовать ряд частот, равномерно распределенных на интервале 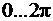 , то есть вплоть до частоты дискретизации. Это может быть необходимо при анализе фильтров с комплексными коэффициентами, частотные характе-ристики которых не являются симметричными. Такое указание дается функции freqzc помощью четвертого входного параметра – строки
, то есть вплоть до частоты дискретизации. Это может быть необходимо при анализе фильтров с комплексными коэффициентами, частотные характе-ристики которых не являются симметричными. Такое указание дается функции freqzc помощью четвертого входного параметра – строки
‘whole’:
freqz(b, a, n, ‘whole’);
Наконец можно задать вектор нормированных круговых частот w для расчета частотной характеристики:
h=freqz(b, a, w);
Использование второго выходного параметра в этом случае не имеет смысла, поскольку вектор частот задан на входе.
При выводе графиков ФЧХ фильтров функция freqz применяет к вектору рассчитанных фазовых сдвигов функцию unwrap, чтобы устранить «фиктивные» разрывы.
Задание на лабораторную работу
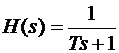 |
Для аналогового прототипа, представляющего собой ФНЧ 1го порядка с передаточной функцией
где Т =1 (т.е. нормированная частота среза Ω=1/ Т =1), cделав подстановку s = j w рассчитать и построить АЧХ аналогового прототипа.
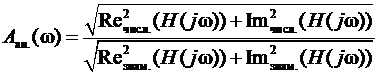
АЧХ:
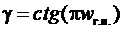 |
С помощью билинейного преобразования
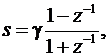
перейти от аналогового прототипа к цифровому фильтру.
| № варианта | w г.п. |
| 0,1 | |
| 0,15 | |
| 0,2 | |
| 0,25 | |
| 0,3 | |
| 0,35 | |
| 0,4 | |
| 0,05 |
Сделав подстановку 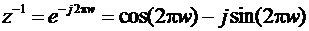 найти и построить АЧХ цифрового фильтра.
найти и построить АЧХ цифрового фильтра.
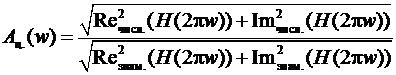
АЧХ:

Для расчета и построения АЧХ аналогового и цифрового фильтров желательно составить программы.
Отчет должен содержать
1. Передаточную функцию аналогового прототипа H (s), ее модуль A ан.(ω) и график АЧХ (привести таблицу с данными для построения АЧХ).
2. Передаточную функцию цифрового фильтра H (z), ее модуль A ц.(w) и график АЧХ (привести таблицу с данными для построения АЧХ).
3. Программу (программы), применявшуюся (применявшиеся) для вычислений.