Основные законы распределения дискретных случайных величин
| Закон распределения | Формула | Математическое ожидание | Дисперсия | Примечание |
| Биномиальный закон распределения |
Вероятность того, что в серии из n независимых испытаний событие A появится ровно k раз (и не появится
q = n-k раз)
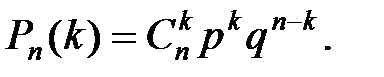 - формула Бернулли
- формула Бернулли
| M(k) = np | D(k) = npq | Испытания происходят в одинаковых условиях и вероятность появления события A в каждом испытании одна и та же и равна p, а q=1-p – противоположное событие. |
| Закон распределения Пуассона | Предельный случай биномиального распределения, где m=np:
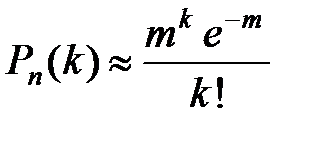
|
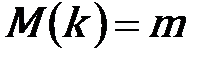
| D(k) = m | Число испытаний n очень велико, а вероятность появления события в каждом отдельном испытании очень мала. Практически формулой Пуассона с достаточной степенью точности можно пользоваться при p < 0,1; m < 10 |
| Геометрическое распределение | 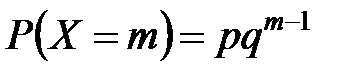
| 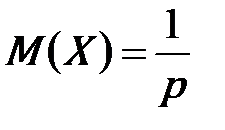
| 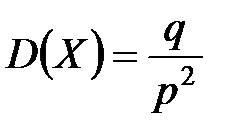
| Испытания заканчиваются, как только событие A появилось. Случайная величина X - число испытаний, которое нужно провести до первого появления события A. |
| Гипергеометрическое распределение | Рассмотрим случайную величину X - число стандартных изделий среди отобранных. Возможные ее значения: 0, 1, 2, …, min{ M, n}. Вероятность того, что среди n отобранных изделий ровно m стандартных:
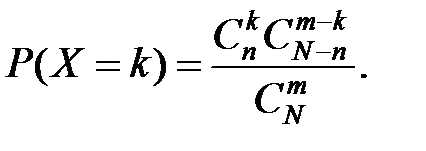
| Закон иллюстрируется задачей: пусть в партии из N изделий имеется M стандартных. Из партии случайно отбирают n изделий, причем отобранные изделия не возвращаются. |
Основные законы распределения непрерывных случайных величин
| Закон распределения | Формула | Математическое ожидание | Дисперсия | Примечание |
| Закон равномерного распределения вероятностей | Плотность вероятностей равномерной случайной величины на отрезке [a, b] постоянна и равна нулю вне этого отрезка:
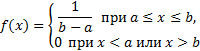 Вероятность попадания равномерно распределенной случайной величины на интервал
Вероятность попадания равномерно распределенной случайной величины на интервал 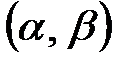 , принадлежащий , принадлежащий 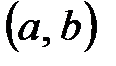 , равна , равна
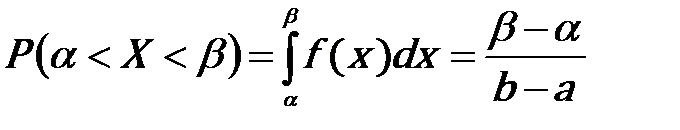
|
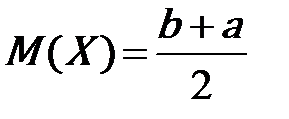
|
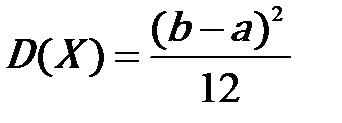
| Примером равномерно распределенной случайной величины является ошибка измерения, которая может принимать с постоянной плотностью вероятности любое значение между двумя целыми делениями прибора. |
| Показательный (экспоненциальный) закон распределения | Непрерывная случайная величина подчинена показательному закону распределения, если ее плотность вероятностей равна
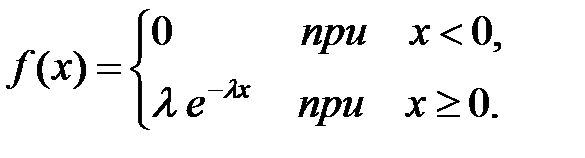 Интегральная функция распределения показательного закона:
Интегральная функция распределения показательного закона:
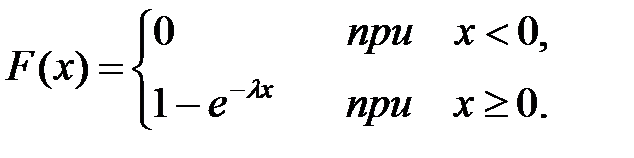 Вероятность попадания на конечный интервал
Вероятность попадания на конечный интервал 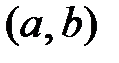 случайной величины, распределённой по показательному закону, равна случайной величины, распределённой по показательному закону, равна
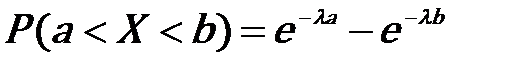
| 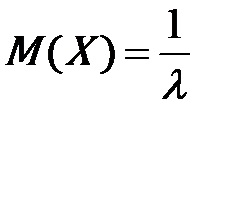
| 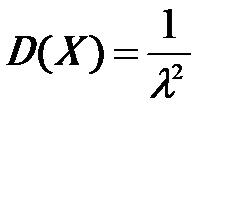
| Примером случайной величины, распределенной по показательному закону, может служить время между появлением двух последовательных событий, наступающих в случайные моменты времени (события простейшего потока). |
| Нормальный закон распределения | Непрерывная случайная величина подчинена нормальному закону распределения (закону распределения Гаусса), если ее плотность вероятностей равна
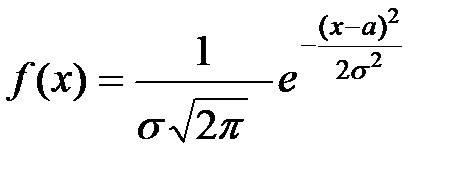 . .
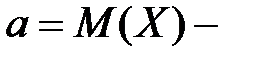 математическое ожидание. математическое ожидание.
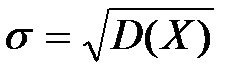 - среднее квадратическое отклонение нормально распределенной случайной величины X.
Вероятность попадания нормально распределенной случайной величины на произвольный конечный интервал ( - среднее квадратическое отклонение нормально распределенной случайной величины X.
Вероятность попадания нормально распределенной случайной величины на произвольный конечный интервал (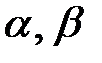 ) равна ) равна
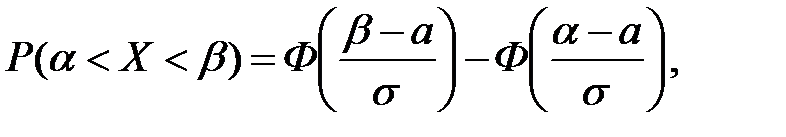 где
где 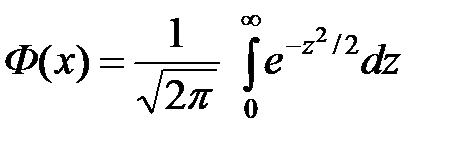 - функция Лапласа - функция Лапласа
| 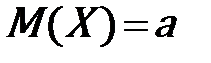
| 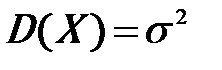
| Является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. |