Физико-механические свойства полимеров
Полимерным материалам свойственны следующие свойства:
1) Способность деформироваться значительно и обратимо
2) Как высокие, так и низкие модули упругости
3) Анизотропия свойств
4) Зависимость свойств полимеров от времени
5) Растворы полимеров обладают аномально высокой вязкостью, существенно отличающейся от вязкости растворов мономеров
3 основных свойства макромолекул:
1) Цепное линейное строение
2) Высокая ММ
3) Слабые взаимодействия между макромолекулами
Характеристики макромолекул:
1) Молекулярная масса и длина макромолекул
2) Конфигурация (определяет строение макромолекул). Существует 3 вида изомерии: локальная, оптическая и цис-транс изомерия
3) Конформация (определяет форму макромолекул)
Конформация – это пространственное расположение атомов и групп атомов, которое создается набором и последовательностью конфигураций, их взаимным расположением в молекуле (обусловленных тепловым движением или внешним воздействием на систему).
Подробнее о характеристиках макромолекул см. лек. №2
Модель макромолекулы. Гибкость макромолекулы.
Макромолекулы практически никогда не находятся в предельно вытянутом положении, она стремится каким-либо образом свернуться, чтобы принять более выгодное состояние (проявляется стремление принять положение, отвечающее минимуму энергии).
Контурной длиной цепи называется длина максимально вытянутой цепи, однако из-за неудобства определения этой величины этой характеристикой пользуются редко.
Рассмотрим молекулы 1,2-дизамещенных производных этана
Молекула 1,2-дихлорэтана:
За 1 секунду эта молекула претерпит 1012 конформаций вследствие теплового движения
Е(φ)
kT
φ
Происходит свободное вращение одной части молекулы относительно другой. На рисунке приведена зависимость энергии Е от угла вращения φ. Минимумы соответствуют транс-конформации, максимумы – цис-конформации. Энергия теплового движения kT может превышать возможную энергию, которую может принять молекула, образуя цис-конформацию.
Пусть заместители будут разными:
,
R1 и R2 – некоторые макрозаместители
Молекула может принимать цис-, транс-, или гош-конформацию (промежуточную конформацию).
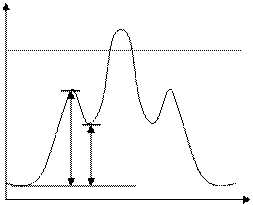
В этом случае зависимость будет следующей:
 |
Е(φ)
kT
ΔU΄ ΔU˝
φ
Цис-конформация часто бывает недоступной, т. к. энергия теплового движения может быть меньше, чем энергия, необходимая для перевода молекулы в это положение.
Возможна некоторая промежуточная выгодная конформация, называемая гош-конформацией. Транс- и гош-конформации определяют возможные изменения макромолекулы. Разность энергий транс- и гош-конформаций представляют собой термодинамическую гибкость макромолекулы (ΔU˝). Разность энергий ΔU΄ представляет собой кинетическую гибкость, т. е. энергетический переход от транс- к гош-конформации. Кинетическая и термодинамическая гибкости макромолекулы являются характеристиками гибкости цепи макромолекулы.
Модели макромолекул:
1) Модель свободно сочлененной цепи (модель ССЦ)
Эта модель является наиболее идеализированным представлением о макромолекуле
Положения, позволяющие построить данное представление:
а) может происходить относительно свободное вращение звеньев друг с другом
б) взаимодействия между заместителями в макромолекуле отсутствуют
в) валентный угол не фиксирован
г) расстояние между атомами строго фиксировано
д) объемами атомов углерода пренебрегают
 |
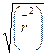
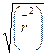- среднее квадратичное расстояние, оно характеризует расстояние между концами цепи
, где N – число звеньев в цепи, а l – длина одного звена
Полная длина цепи представляет собой произведение этих величин:
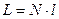
Макромолекулу можно характеризовать степенью свернутости:
степень свернутости представляет собой потенциальную возможность изменения размеров макромолекулы
Количество звеньев эквивалентно степени полимеризации, поэтому при увеличении степени полимеризации возможности изменения размеров увеличиваются.
Пример: при степени полимеризации 102 макромолекула может изменять свой размер в 10 раз, при 104 – в 100 раз.
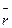соответствует наиболее вероятному значению r, т. е. среднему значению
Распределение макромолекул по значениям среднего квадратичного расстояния между концами цепи является гауссовым
W(r)
rmax r
поэтому клубок, образуемый макромолекулой часто называют гауссовым клубком
Среднее расстояние равно:
2) Модель с фиксированным валентным углом
Модель представляется в следующем виде:
 |
θ
α
1 3
вращение происходит свободно, но только по образующим конуса
Среднее расстояние равно в этом случае:
, поэтому можно заключить, что по сравнению с предыдущей моделью клубок немного разбухает, жесткость молекулы увеличивается
3) Модель с заторможенным вращением
Эта модель аналогична предыдущей модели, вводится лишь положение о том, что происходит заторможенное вращение, некоторые конформации недоступны из-за того, что энергии теплового движения недостаточно для их реализации.
Поэтому вводится поправка, учитывающая углы заторможенного вращения, при которых реализуются возможные конформации:
