ФИЗИЧЕСКИЕ ОСНОВЫМЕХАНИКИ»
Основные формулы
1.1. Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси X:
где 
- некоторая функция времени.
1.2 Средняя путевая скорость
где 
- путь, пройденный точкой за интервал времени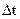 
. Путь, в отличие от разности координат 
, не может убывать и принимать отрицательные значения, т.е. 
.
1.3 Мгновенная скорость
.
1.4 Тангенциальное a τ, нормальное a n и полное a ускорения.
где r - радиус кривизны траектории (в частности, радиус окружности на которой проходит движение).
1.5 Для равноускоренного прямолинейного движения (например, вдоль координат оси X).
где 
- проекции на ось X векторов скорости, начальной скорости, ускорения и перемещения.
1.6 Кинетическое уравнение движения материальной точки по окружности
где 
- угол поворота радиус-вектора движущейся точки.
1.7 Угловая скорость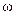 
и угловое ускорение 
1.8 Для равноускоренного движения по окружности
где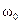 
- начальная угловая скорость.
1.9 Взаимосвязь между линейными и угловыми характеристиками движения точки по окружности
1.10 Частота вращения n и число сделанных оборотов N твердого тела
где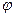 
- угол поворота.
1.11 Импульс материальной точки, а также тела, движущегося поступательно
где m- масса тела.
1.12 Второй закон Ньютона (основной закон динамики поступательного движения)
.
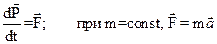1.13 Силы, рассматриваемые в механике:
а) сила упругости
,
где k - жесткость пружины, x - удлинение (укорочение) пружины;
б) сила тяжести
,
где g - ускорение свободного падения;
в) сила гравитационного взаимодействия
,
где G - гравитационная постоянная; m1 и m2 - массы взаимодействующих тел, r - расстояние между телами (тела рассматриваются как материальные точки).
|
|
г) сила трения (скольжения)
,
где 
- коэффициент трения; N - сила нормального давления.
1.14 Закон сохранения импульса
или для двух тел (
)
где 
и 
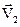- скорости тел в момент времени, принятый за начальный; 
и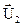 
- скорости тех же тел в момент времени, принятый за конечный.
1.15 Кинетическая энергия тела, движущегося поступательно
1.16 Потенциальная энергия:
а) упруго деформированной пружины
где k - жесткость пружины; x - абсолютная деформация;
б) гравитационных взаимодействий
где G - гравитационная постоянная; m1 и m2 - масса взаимодействующих тел; r - расстояние между ними (тела рассматриваются как материальные точки);
в) тела, находящегося в поле силы тяжести,
,
где g - ускорение свободного падения; h - высота тела над уровнем принятым за нулевой (формула справедлива при условии A<<R, где R - радиус Земли).
1.17 Закон сохранения механической энергии
.
1.18 Работа, совершаемая внешними силами, определяется как мера изменения энергии системы
.
1.19 Работа, совершаемая силой F на пути от точки 1 до точки 2,
,
где 
- элементарный вектор перемещения; 
- модуль перемещения; α - угол между силой F и перемещением ; 
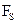- проекция силы на направление перемещения. При 
.
1.20 Мощность
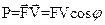
где F - сила; V - скорость; φ - угол между векторами силы и скорости.
1.21 Момент инерции некоторых тел массой m относительно оси z проходящих через центр масс:
а) стержня длинной l относительно оси, перпендикулярной стержню
|
|
;
б) обруча (тонкостенного цилиндра) радиусом R относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра)
;
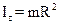в) диска радиуса R относительно оси, перпендикулярной плоскости диска 
.
1.22 Момент инерции относительно произвольной оси I равен (теорема Штейнера)
,
где 
- момент инерции относительно оси, параллельной данной и проходящей через центр масс тела; a - расстояние между осями; m -масса тела.
1.23 Момент импульса тела, вращающегося относительной неподвижной оси z
.
1.24 Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси:
,
где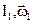 
и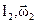 
- моменты инерции системы тел и угловые скорости вращения в моменты времени, принятые за начальный и конечный.
1.25 Момент силе F относительно точки O (вращающий момент)
,
где r - радиус-вектор точки приложения силы.
Модуль вращающего момента
где F - модуль силы; l -плечо силы (длина перпендикуляра, опущенного из точки O на прямую, вдоль которой действует сила).
Момент силы относительно произвольной оси z, проходящей через точку O, является проекцией вращающего момента (т.е. момента силы относительно точки) на эту ось z:
.
.
При Iz=const, Mz=Ize.
1.26 Основной закон динамики вращательного движения относительно неподвижной оси z:
, при Iz=const, Mz=Ize.
1.27 Кинетическая энергия тела, вращающегося вокруг неподвижной оси:
.
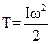1.28 Кинетическая энергия тела при плоско-параллельном движении (состоящем из поступательного и вращательного движения)
.
1.29 Работа, совершаемая внешней силой при вращении твердого тела:
,
где Mz - момент силы относительно оси вращения z;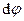 
-элементарный угол поворота.
|
|
1.30 Мощность при вращении
,
где 
- проекция вектора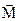 
на направление вектора угловой скорости.
1.31 Кинематическое уравнение гармонических колебаний материальной точки:
где x -смешение; A - амплитуда колебаний;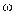 
- круговая или циклическая частота; 
- начальная фаза.
1.32 Скорость и ускорение материальной точки совершающей гармонические колебания:
;
.
1.33 Частота ν, период Т и циклическая частота ω связаны между собой формулами
.
1.34 Квазиупругая сила, действующая при гармонических колебаниях F и коэффициент квазиупругой силы k:
,
где x - смешение колеблющейся точки; m - её масса; 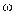- циклическая частота.
1.35 Потенциальная П, полная E и кинетическая энергия колеблющейся материальной точки:
где А - амплитуда колебаний.
1.36 Период колебаний математического маятника
,
где l - длина маятника; g-ускорение свободного падения.