ЗАДАЧА 5.1.
Заданы функция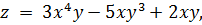 
точка 
и вектор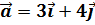 
. Найти:
1) частные производные, 2) градиент функции z в точке А и его модуль, 3) производную функции z в точке А по направлению вектора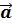 
.
Решение:
1) Найдем частные производные первого порядка функции z(x, y):
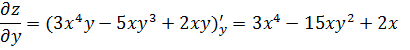
2) Градиент функции z(x, y) называется векторная функция:
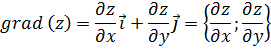
Найдем значение частных производных первого порядка функции z(x, y) в точке А (-2; 1):
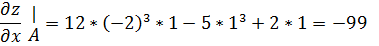
Тогда градиент в точке А равен:
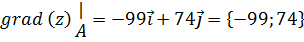
3) Производная функция z по направлению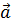 
- это алгебраическая проекция вектора 
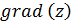на направление :
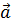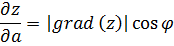
где φ – угол между векторам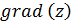и и .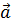
Поскольку
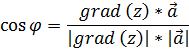
то в точке A получаем:
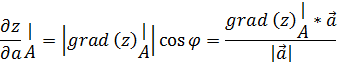
Подставляем все числовые данные:
Ответ:
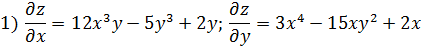
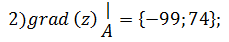
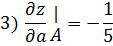
ЗАДАЧА 5.2
Исследовать функцию двух переменных на экстремум.
а) z=3x2-xy+2y-4
Найдем первые частные производные:
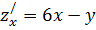
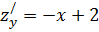
Приравняем их к нулю:
-x+2=0 ⇒ x=2
6x-y=0 ⇒ y=6x=6∙2=12
x=2, y=12
Точка (2; 12) является критической на экстремум. Проверим, существует ли он.
Найдем вторые производные:
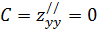
Вычислим Δ=AC-B2=6∙0-1=-1<0. Так D<0, то экстремума не существует.
б) z=3x2+5y2-10xy+14x-10y
Найдем первые частные производные:
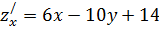
Приравняем их к нулю:
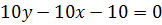
Или:
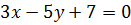
Решим полученную систему уравнений:
x=1
y=2
Точка (1; 2) является критической на экстремум. Проверим, существует ли он.
Найдем вторые производные:
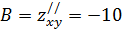
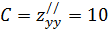
Вычислим Δ=AC-B2=6∙10-(-10)2=60-100=-40<0. Так D<0, то экстремума не существует.
ЗАДАЧА 6.1
Найти неопределенные интегралы.
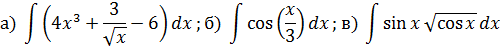
Решение:
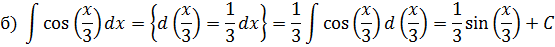
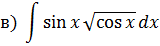
внесем под знак дифференциала:
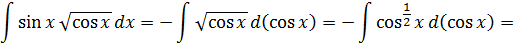
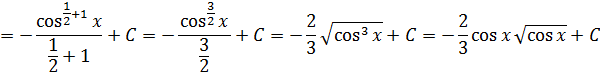
Ответ: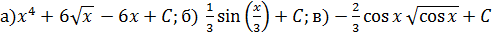 
ЗАДАЧА 6.2
Найти площадь фигуры, ограниченной линиями.
Решение:
Площадь фигуры, расположенной между двумя линиями находится по формуле:
где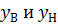 
– уравнения соответственно верхней и нижней линий, ограничивающих фигуру; а и b–точки пересечения линий. Найдем точки пересечения этих линий, для чего приравняем правые части уравнений:
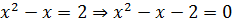
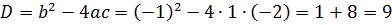
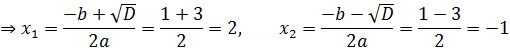
Построим линии между точками пересечения, для чего зададим несколько значений x и найдем соответствующие y.
1) 
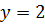, это прямая, параллельная оси Ox.
2) 
- это парабола, возьмем несколько точек.
| x | -2 | -1 | 0,5 | ||||
| y | -0,25 |
Из рисунка видим, что
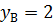
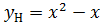
Найдем площадь:
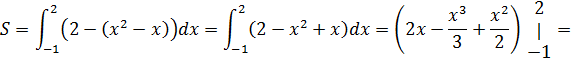
Ответ: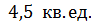 
ЗАДАЧА 7.1
Выполнить действия с комплексными числами
Решение:
а) Переведем оба числа в алгебраическую форму, используя тригонометрическую форму записи:
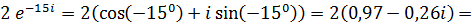
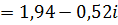
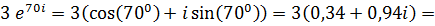
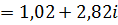
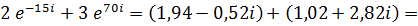
Б) деление комплексных чисел в показательной форме производится следующим образом:
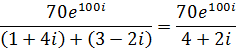
Далее преобразуем знаменатель в показательную форму:
Найдем модуль:
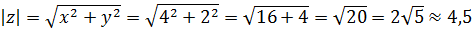
Аргумент найдем по формуле:
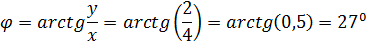
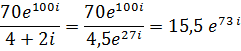
Ответ: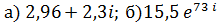 
ЗАДАЧА 7.2
Решить уравнения.
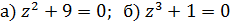
Решение:
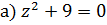
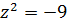
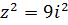
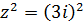
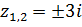
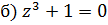
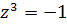
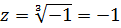
Ответ: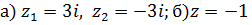 
ЗАДАЧА 8.1
Решить дифференциальные уравнения.
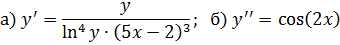
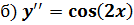
Решение:
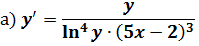
Разделим переменные:
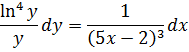
Интегрируем обе части:
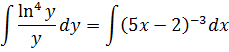
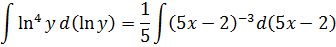
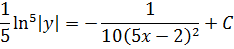
Получили общее решение дифференциального уравнения:
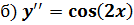
Сделаем замену:
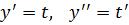
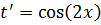
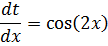
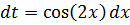
Интегрируем обе части:
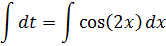
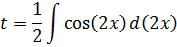
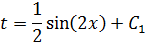
Возвращаемся в замену: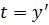 
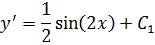
Интегрируем обе части:
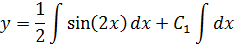
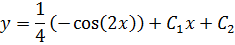
Общее решение дифференциального уравнения:
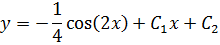
в) y¢¢-25y¢=2sin4x-cos4x
Составляем характеристическое уравнение:
k2-25k=k(k-25)=0 ⇒
⇒ k1=0 и k2=25-вещественные корни характеристического уравнения
Общее решение однородного дифференциального уравнения y ¢¢- 25y ¢ =0 имеет вид:
y0(x)=C1+C2e25x
Частное решение неоднородного дифференциального уравнения ищем в виде:
U(X)=Asin4x+Bcos4x
U'(x)=4Acos4x-4Bsin4x
U''(x)=-16Asin4x-16Bcos4x
U''(x)-25U'(x)=-16Asin4x-16Bcos4x-100Acos4x+100Bsin4x=
=sin4x(100B-16A)+cos4x(-100A-16B)= 2sin 4x -cos4x
-16A+100B=2
-100A-16B=-1
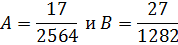
Частное решение неоднородного дифференциального уравнения:
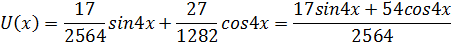
Общее решение неоднородного дифференциального уравнения:
y(x)=y0(x)+U(x)
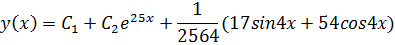
г) 2y¢¢+2y¢+y=4x2
Составляем характеристическое уравнение:
2k2+2k+1=0 ⇒
Получили пару комплексных корней характеристического уравнения.
Тогда общее решение однородного дифференциального уравнения
2y¢¢+2y¢+y =0 имеет вид:
y0(x)=C1e-x/2sin(x/2)+C2e-x/2cos(x/2)
Частное решение неоднородного дифференциального уравнения ищем в виде:
U(X)=Ax2+Bx+C
U'(x)=2Ax+B
U''(x)=2A
2U''(x)+2U'(x)+U(x)=4A+4Ax+2B+Ax2+Bx+C= Ax2+x(4A+B)+4A+2B+C=x2
A=1
4A+B=4+B=0 ⇒ B=-4
4A+2B+C=4-8+C=C-4=0⇒ C=4
Частное решение неоднородного дифференциального уравнения:
U(X)=x2-4Bx+4
Общее решение неоднородного дифференциального уравнения:
y(x)=y0(x)+U(x)
y(x)= C1e-x/2sin(x/2)+C2e-x/2cos(x/2)+ x2-4Bx+4