ЛАБОРАТОРНАЯ РАБОТА №2
Цель работы
1. Получить временные и частотные характеристики типовых динамических звеньев;
2. Изучить влияние изменения параметров передаточных функций на вид этих характеристик.
Постановка задачи
В качестве объекта исследования выступают типовые динамические звенья:
1. Позиционные (апериодическое, колебательное);
2. Интегрирующие (идеальное, с запаздыванием, изодромное);
3. Дифференцирующие (идеальное, с запаздыванием).
Необходимо получить:
1. Передаточные функции исследуемых звеньев;
2. Переходные характеристики исследуемых звеньев;
3. Импульсные переходные характеристики;
4. Логарифмические переходные характеристики;
5. Амплитудно-фазовые характеристики исследуемых звеньев;
6. Анализ влияния на временные и частотные характеристики величины коэффициента усиления и постоянных времени.
Сведения из теории.
Типовые динамические звенья подразделяют на 3 основные группы:
1. Звенья статического или позиционного типа, где 
, 
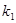- коэффициент передачи звена.
2. Звенья интегрирующего типа, где 
3. Звенья дифференцирующего типа, где 
. Дифференцирующие звенья еще называют форсирующими.
Все статические звенья в установившемся режиме описываются одинаковым уравнением 
. К таким звеньям относятся: статическое идеальное (усилительное), апериодическое, колебательное и консервативное.
Линейное дифференциальное уравнение апериодического звена:
,
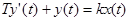где Т – постоянная времени звена;
k – коэффициент усиления.
Примером такого звена может служить любая цепочка, включающая сопротивление и емкость независимо от их физической природы.
Постоянная времени Т зависит от величины сопротивления и емкости и характеризует инерционность звена, причем, чем больше сопротивление и емкость, тем больше постоянная времени и больше инерционность.
Передаточная функция получается из уравнения звена:
Уравнение статического колебательного звена II-го порядка:
,
где 
- постоянные времени, k – коэффициент усиления.
Уравнение установившегося статического режима этого звена имеет тот же вид, что и для усилительного и апериодического звеньев:
Передаточная функция определяется после преобразования по Лапласу:
Введем условное обозначение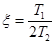 
.
Если выполняется условие ξ < 1, то звено является колебательным, если ξ > 1, то мы имеем дело с апериодическим звеном II-го порядка, которое описывается тем же уравнением, что и колебательное звено.
В интегрирующих звеньях выходной сигнал пропорционален интегралу от входного.
Уравнение идеального интегрирующего звена имеет вид:
Передаточную функцию интегрирующего звена получим после преобразования этого уравнения по Лапласу:
.
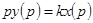
Интегрирующее звено с запаздыванием описывается дифференциальным уравнением
.
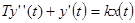Передаточная функция звена:
.
Изодромное звено описывается уравнением
.
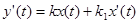Передаточная функция звена
,
где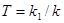 
- постоянная времени изодромного звена.
Из этих выражений видно, что звено можно условно представить в виде совокупности двух звеньев, действующих параллельно, - идеального интегрирующего с коэффициентом передачи k и безынерционного с коэффициентом передачи k1.
Выходной сигнал дифференцирующих звеньев пропорционален дифференциалу от входного сигнала.
Идеальное дифференцирующие звено описывается уравнением
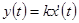
То есть изменение выходной координаты звена пропорционально скорости изменения входной координаты. Параметр k называют постоянной дифференцирования (измеряется в секундах)
В операторной форме уравнение записывается в виде: 
, откуда найдем передаточную функцию и, поле соответствующих преобразований, частотной характеристики:
.
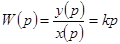Дифференцирующие звено с запаздыванием описывается уравнением следующего вида.
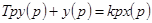
Передаточная функция:
.
Последовательность выполнения работы.
Для выполнения лабораторной работы используется пакет прикладных программ (ППП) Control System Toolbox. ППП предназначен для работы с LTI-моделями (Linear Time Invariant Models) систем управления.
Все необходимые характеристики типовых звеньев могут быть получены с помощью уже известных команд: step, impulse, bode, nyquist, или с помощью команды ltiview.
Выполнение работы осуществляется в следующей последовательности:
1. Изучить теоретические сведения.
2. Запустить систему MATLAB.
3. С помощью команды tf получить передаточные функции апериодических звеньев с различными коэффициентами усиления в соответствии с заданным вариантом.
4. С помощью команд step, impulse, bode, nyquist определить временные и частотные характеристики апериодического звена, сделав анализ влияния коэффициента усиления.
5. С помощью команды tf получить передаточные функции апериодических звеньев с различными постоянными времени Т в соответствии с заданным вариантом.
6. С помощью команд step, impulse, bode, nyquist определить временные и частотные характеристики апериодического звена, сделав анализ влияния величины постоянной времени Т.
7. Аналогично получить передаточные функции и динамические характеристики для колебательного, интегрирующих и дифференцирующих звеньев.
Методический пример.
Дана передаточная функция апериодического звена:
; k = 2; T = 2.
Определим его временные и частотные характеристики.
1. Создадим LTI-объекты w1, w2, w3 с различными значениями k:
>> k=2;
>> T=2;
>> w1=tf([k],[T,1])
>> w2=tf([k*2],[T,1])
>> w3=tf([k*4],[T,1])
2. Построим для полученных передаточных функций динамические характеристики, используя команды step, impulse, bode, nyquist:
>> step(w1,w2,w3):
>> impulse(w1,w2,w3):
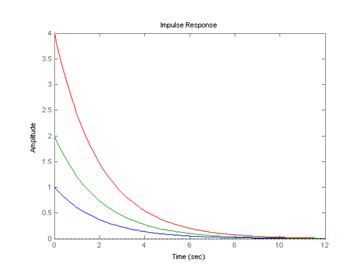
>> bode(w1,w2,w3):
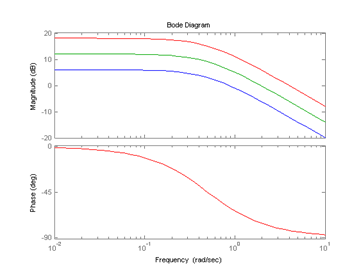
>> nyquist(w1,w2,w3);
3. Создадим LTI-объекты h1, h2, h3 с различными значениями постоянной времени Т:
>> h1=tf([k],[T,1]);
>> h2=tf([k],[2*T,1]);
>> h3=tf([k],[4*T,1]);
4. Аналогично п.2 для найденных передаточных функций получим динамические характеристики:
>> step(h1,h2,h3);
>> impulse(h1,h2,h3);
>> bode(h1,h2,h3);
>> nyquist(h1,h2,h3);
5. Исследуем влияние изменения параметров колебательного звена на его временные и частотные характеристики.
Создадим передаточные функции звена в соответствии с заданным вариантом, изменяя коэффициент усиления:
; k = 2; T1 = 1.5; T2=2.
>> w1=tf([k],[4,1.5,1]);
>> w2=tf([k*2],[4,1.5,1]);
>> w3=tf([k*4],[4,1.5,1]);
6. Получим динамические характеристики:
>> step(w1,w2,w3):
>> impulse(w1,w2,w3):
>> bode(w1,w2,w3):
>> nyquist(w1,w2,w3):
7. Изменим значения постоянных времени в передаточной функции:
Т1 = 4, Т2 = 1.5.
>> w1=tf([k],[1.5,4,1]);
Для сравнения возьмем исходную передаточную функцию колебательного звена:
>> w2=tf([k],[4,1.5,1]);
8. Построим динамические характеристики.
>> step(w1,w2):
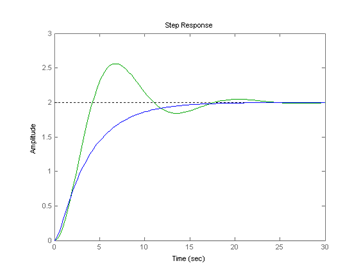
>> impulse(w1,w2):
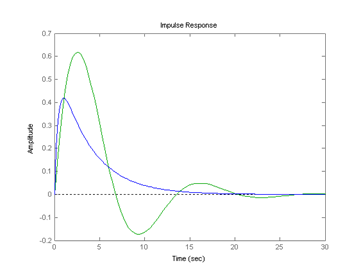
>> bode(w1,w2):
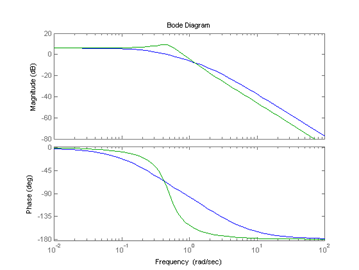
>> nyquist(w1,w2):
Варианты заданий.
Вид передаточной функции:
1. 
;
2. 
;
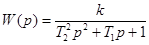3. 
;
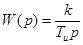4. 
.
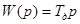| № варианта | k | T | T1 | T2 | Tи,Tд |
| 1. | |||||
| 2. | 3.5 | ||||
| 3. | |||||
| 4. | 7.2 | ||||
| 5. | 3.5 | 1.5 | |||
| 6. | 1.3 | ||||
| 7. | 2.7 | ||||
| 8. | 2.2 | ||||
| 9. | 2.5 | 5.5 | |||
| 10. | 1.5 | ||||
| 11. | 1.3 | 1.8 | 8.1 | ||
| 12. | 2.7 |
Контрольные вопросы
1. Приведите пример временных характеристик апериодического звена I-го порядка.
2. Как меняются временные характеристики статических звеньев с изменением коэффициента усиления звена?
3. Как меняются временные характеристики статических звеньев с изменением коэффициента усиления звена?
4. Как отличить колебательное звено от апериодического звена II-го порядка по виду передаточной функции?
5. Приведите пример частотных характеристик интегрирующего звена с запаздыванием.
6. Как меняются частотные характеристики интегрирующего звена при изменении постоянной времени?
7. Приведите пример логарифмических частотных характеристик дифференцирующих звеньев.
8. Как изменятся характеристики дифференцирующих звеньев при изменении коэффициента усиления?