Первый вид формальной модели алгоритма основан на представлении об алгоритме, как о программе для некоторого детерминированного устройства. Одним из таких устройств является одноленточная детерминированная машина Тьюринга (ДМТ), которая представляет собой логическое устройство, состоящее из:
1) неограниченной в обе стороны ленты, разделенной на одинаковые пронумерованные ячейки;
2) читающей/пишущей головки;
3) управляющего устройства с конечным числом состояний.
Программу 
для ДМТ определяют следующие компоненты:
1) G – конечное множество символов, записываемых на ленте, 
– множество входных символов,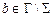 
– выделенный пустой символ;
2) Q – конечное множество состояний, в котором выделено начальное состояние 
и два конечных – 
;
3) функция переходов 
.
Т.е. 
.
Задание 1. Построить ДМТ-программу, которая копирует на ленте заданное натуральное число.
Решение. Как задача распознавания эта задача звучит следующим образом: существует ли копия заданного натурального числа.
Для представления натурального числа будем использовать символ 1, при такой схеме кодирования число n записывается в виде последовательности из n единиц. Для разделения исходного числа и копии используем символ *, в качестве вспомогательного символа выберем 0. Таким образом, 
, 
.
Отрицательный ответ в данной задаче при такой схеме кодирования будет только в случае, когда лента пуста или в записи исходного числа присутствуют символы, отличные от 1.
Копирование числа n будем выполнять за n проходов с возвратом. На каждом проходе заменим первую нескопированную единицу на вспомогательный символ 0, затем, двигаясь вправо, дойдём до конца записи, повторяя все символы, стоящие перед пустым, и запишем 1 в конец записи. Во время первого прохода перед записью 1 нужно вставить разделительный символ *. Затем будем двигаться влево, также повторяя символы, до тех пор, пока не достигнем 0, после чего действия повторяются. Когда все единицы будут скопированы (после символа 0 стоит *), нужно восстановить исходное число, заменив все 0 на 1, двигаясь влево.
Построим вначале ориентированный граф, соответствующий функции переходов, которая реализует последовательность действий, описанных выше. Затем выпишем множество состояний и табличное задание функции переходов. Вершинами графа будут являться состояния управляющего устройства, дуги графа означают переход из одного состояния в другое, причём, над каждой дугой будем писать символ(ы), по которому выполняется переход, а после знака ® – замещающий символ(ы) и на 
правление движения головки.
Следовательно, 
.
Функцию переходов представим в виде таблицы, содержащей значения 
.–
| q | s | |||
| * | b | |||
| q 0 | (qN, b, 1) | (q 1, 0, 1) | (qN, b, 1) | (qN, b, 1) |
| q 1 | (qN, b, 1) | (q 1, 1, 1) | (qN, b, 1) | (q2, *, 1) |
| q 2 | – | – | – | (q3, 1, -1) |
| q 3 | (q4, 0, 1) | (q3, 1, -1) | (q3, *, -1) | – |
| q 4 | – | (q5, 0, 1) | (q6, *, -1) | – |
| q 5 | – | (q5, 1, 1) | (q5, *, 1) | (q3, 1, -1) |
| q 6 | (q6, 1, -1) | – | – | (qY, b, 1) |
Второй подход основан на понятии вычисления и числовой функции, основная теоретическая модель этого вида – рекурсивные функции.
Работу ДМТ-программы можно рассматривать, как вычисление некоторой функции 
. Если слово 
и программа останавливается на любом входе из S*, то результатом вычисления 
будет слово, составленное из символов, записанных на ленте после остановки машины в ячейках с 1-ой по последнюю непустую ячейку.
Классом функций, для которых вычисляющий их алгоритм существует, являются частично-рекурсивные функции.
Функция называется частично рекурсивной, если она может быть построена из 0, функций 
и 
с помощью конечного числа применений операторов суперпозиции, примитивной рекурсии и m-оператора.
Задание 2. Доказать примитивную рекурсивность следующих функций:
1) 
;
2) 
;
3) 
;
4) 
;
5) 
.
Решение.
1)
2)