Автоматическое доказательство теорем методом резолюций

Алгоритм, который проверяет соотношение G |-_T S для формулы S, множества формул G и теории T называется алгоритмом автоматического доказательства теорем. Для прикладных исчислений первого порядка такое доказательство проводится методом резолюций.

Метод резолюций работает со стандартной формой формул, называемой предложениями. Предложением называется бескванторная дизъюнкция литералов. Любая формула исчисления предикатов может быть преобразована в множество предложений по следующему алгоритму.

1. Построить предварённую нормальную форму формулы. Напомним, что для этого нужно:

a) преобразовать формулу к приведённому виду, т.е. исключить операцию ® и спустить операцию отрицания до атомарных формул;

b) провести разделение связанных переменных;

c) вынести операции связывания переменных в начало формулы.

2. Преобразовать предварённую нормальную форму в предклазуальную, т.е. привести матрицу U нормальной формы к КНФ.

3. Провести сколемизацию нормальной формы (построить клазуальную нормальную форму, исключив операции связывания переменных).

4. Удалить операции Ù (дизъюнкции клазуальной нормальной формы составят искомое множество предложений).

Далее к предложениям, полученным из формул множества G и из формулы Ø S, применяется правило резолюции.

Определение. Пусть – предложения исчисления предикатов, такие что , , 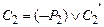а атомарные формулы унифицируемы наиболее общим унификатором t. Правило вывода

называется правилом резолюции исчисления предикатов, предложения – резольвируемыми, а – резольвентой.

Таким образом, множество предложений будет являться противоречивым, если в результате последовательного применения правила резолюции, получим пустую формулу, которую будем обозначать š. Действительно, если резольвента пуста, то резольвируемые предложения – взаимно противоположные высказывания и система предложений противоречива.

Работа метода резолюций может иметь следующие варианты результатов:

1) на очередном шаге получено пустое предложение и, следовательно, формула S является следствием G (теорема 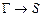доказана);

2) если во множестве предложений нет новых резольвируемых предложений, то теорема опровергнута;

3) множество предложений постоянно пополняется новыми предложениями (зацикливание), что означает, что средств данной теории недостаточно ни для того, чтобы доказать теорему, ни для того, чтобы её опровергнуть.

Представим алгоритм работы метода резолюций на языке описания алгоритмов. Результат 1 – если S выводимо из G, 0 – в противном случае. Обозначим M – множество предложений, C – множество предложений, полученное из G и Ø S. Функция choose выполняет выбор резольвируемых предложений, R – вычисляет резольвенту.

while ÿÏ C

begin choose ()

if then return 0

R()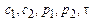

end

return 1

В качестве примера рассмотрим проверку выводимо ли утверждение дядя(cергей, Y) из множества предложений «Родственные отношения» (см. задания для РПР).

Добавим в множество предикат

дядя(X, Y) X – дядя Y

и правило вывода

дядя(X, Y) род(Z, Y) Ù брат(X, Z).

Запишем это правило в виде предложения

82. дядя(X, Y) Ú Ø род(Z, Y) Ú Øбрат(X, Z).

Добавим в множество предложений отрицание проверяемого утверждения

83. Ø дядя(cергей, Y)

и будем применять к предложениям множества правило резолюции.

Таким образом, предложение дядя(cергей, Y) выводимо из заданного множества предложений при Y=павел.