Добавление к заданию 6-7.04.20 по электротехнике по результатам первых ответов.
Студенты, приславшие первые ответы на выданное задание по расчёту электрических цепей переменного тока, дружно показали не понимание материала, а именно: векторной диаграммы правил её построения ну и конечно её значения для расчётов и методов расчёта с применением комплексных чисел.
Векторная диаграмма.
Как сказано в учебнике, кроме графического изображения (осциллограммы) переменного тока всем до боли знакомой синусоиды, имеется векторное изображение.
Это изображение очень полезно и наглядно для иллюстрации сдвига фаз между напряжениями и токами в разных точках электрической схемы.
Правила построения векторной диаграммы следующие:
1. Вектора, отображающие напряжение, ток или мощность, вращаются по окружности против часовой стрелки со скоростью круговой частотой ω=2·π·f.
2. Вектор, опережающий другой вектор на угол φ, будет изображаться опережающим основной вектор, с которым этот фазовый угол сравнивается. То есть он уйдёт влево.
3. Вектор, отстающий от другого вектора на угол φ, будет изображаться отстающим от основного вектора, с которым этот фазовый угол сравнивается. То есть он уйдёт вправо.
4. Для простых электрических цепей, одно активное сопротивление, одна ёмкость, одна индуктивность, последовательно/параллельно включенные пары активное сопротивление - ёмкость, активное сопротивление - индуктивность или колебательный контур - активное сопротивление - индуктивность – ёмкость, векторная диаграмма простая, представляет прямоугольный треугольник и расчёты можно проводить с помощью формулы Пифагора и понятий тригонометрии. Здесь я сознательно пользовался терминами: активное сопротивление, индуктивность, ёмкость, так как это могут быть не детали (резистор, конденсатор, катушка индуктивности), а, например, входное сопротивление транзистора, входная ёмкость транзистора, индуктивность выводов транзистора и т.д.
В вашей работе векторные диаграммы необходимо строить на миллиметровке со соблюдением масштаба и выверкой углов по транспортиру. Тогда я пойму, что вы разобрались с векторной диаграммой и оценки будут совсем другие.

Работа с комплексными числами.
При расчётах электрических цепей на переменном токе необходимо пользоваться комплексными числами.

Иерархия чисел
Комплексное число состоит из вещественного числа (всегда и везде мы его применяем) и мнимого числа, в свою очередь состоящего из вещественного коэффициента при мнимом числе, за которое принят √(-1) (корень из минус единицы).
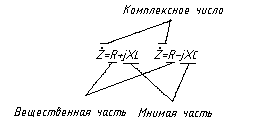
Комплексные числа имеют несколько видов записи:
1. Алгебраическая форма: Z =R+j·X;
2. Тригонометрическая форма: (sinφ+j·cosφ), где: z=√(R2+X2) модуль комплексного сопротивления.
3. Показательная форма: Z =z·e-jφ.
4. Геометрическая форма:

Связь между этими формами записи следующая:
R=z·sinφ, X= z·cosφ, z=√(R2+X2), φ=arctg(X/R), z=√(R2+X2).
В настоящем тексте вместо точки на символом обозначающей комплексное число применено подчёркивание.
Арифметические действия с комплексными числами.
Z1=R1+jX1,
Z2= R2+jX2
Сложение.
Z1 + Z2 = R1+jX1+R2+jX2 = (R1+ R2)+j(X1+ X2)
Вычитание.
Z1 - Z2 = R1+jX1-R2+jX2 = (R1- R2)+j(X1- X2)
Умножение
Z1 · Z2 = (R1+jX1)·(R2+jX2) = R1 · R2+jX1 · R2+jX1 · R2+j2X1 · X2 = (R1 · R2- X1 · X2)+ j (X1 · R2+ X1 · R2)
Умножение удобно делать в показательном виде
Z1 · Z2 =z1e-jφ1·z2e-jφ2= z1·z2e-j (φ1+φ2)
Деление
Z1 / Z2 = 
Деление удобно делать в показательном виде
Z1 / Z2 =z1e-jφ1/z2e-jφ2= z1/z2e-j (φ1-φ2)
Сопряжённые комплексные числа: Z1=R1+jX1,Z1=R1-jX1.
Если этой информации по комплексным числам будет недостаточно, для ваших услуг интернет.