Доказательство того, что некоторое утверждение D эквивалентно (равносильно) V-му постулату Евклида заключается в следующем: следует доказать, что из аксиом абсолютной геометрии (т.е. аксиом 1-1V групп) и V-го постулата Евклида следует утверждение D, и наоборот, из аксиом абсолютной геометрии и утверждения D следует V-й постулат Евклида.
Если про некоторое утверждение D1 доказано, что оно эквивалентно V-му постулату Евклида, то утверждение D эквивалентно V-му постулату Евклида, если оно эквивалентно утверждению D1.
Наиболее известны следующие эквиваленты V постулата:
1. Через точку, не лежащую на прямой а, проходит не более одной прямой, параллельной прямой а.
2. Через точку А, не лежащую на прямой а, проходит единственная прямая, параллельная а.
3. Сумма углов любого треугольника равна 2d.
4. Существует хотя бы один треугольник, сумма углов которого равна 2d.
5. Если в четырехугольнике АВСD углы А и В прямые, стороны АD и ВС конгруэнтны, то стороны АВ и СD также конгруэнтны.
6. Множество всех точек полуплоскости с границей а и равноудаленных от а, есть прямая.
7. Если две прямые не перпендикулярны, то любая прямая, перпендикулярная одной из них, пересекает другую прямую.
8. Если дан произвольный отрезок и произвольный острый угол, то существует прямоугольный треугольник, один из катетов которого равен данному отрезку, а прилежащий угол равен данному углу.
9. Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
10. Если прямая проходит через внутреннюю точку угла и не содержит вершину угла, то она пересекает хотя бы одну сторону угла.
11. Вокруг любого треугольника можно описать окружность.
|
|
Теорема. Пятый постулат Евклида эквивалентен аксиоме параллельности(Евклида): «Через точку, не лежащую на прямой а, проходит не более одной прямой, параллельной прямой а».
Доказательство.
(Þ) Пусть выполняется аксиома параллельности(Евклида).
И пусть даны две прямые АВ и СD, их секущая ХY (Х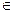 
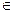АВ, Y СD) и точки В, D лежат по одну сторону от прямой ХY, причем Ð ХYD + Ð YХВ < 2 d. Так как Ð YХА + Ð YХВ = 2 d, то Ð YХА > Ð ХYD, значит существует внутренний луч ХМ угла YХА такой, что Ð YХМ @Ð ХYD, тогда из следствия к теореме 4.1 получим, что прямые МХ и СD не пересекаются. Тогда из аксиомы Евклида следует, что
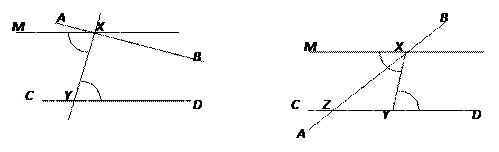
прямые АВ и СD пересекаются в точке Z.
Предположим, что точка Z принадлежит лучу YС, тогда ХZ – внутренний луч угла YХМ, поэтому 
YХМ >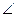 
YХZ. Но ХYD – внешний угол треугольника ХYZ, а угол YХZ – угол этого треугольника, не смежный с углом ХYD. Мы получили противоречие с теоремой о внешнем угле треугольника. Следовательно, точка Z пересечения прямых АВ и СD принадлежит лучу YD.
(Ü) Пусть выполняется пятый постулат Евклида. В плоскости α дана прямая СD и точка А, не принадлежащая этой прямой. Из теоремы 3.9 следует, что в плоскости α существует перпендикуляр АН к прямой СD. Из той же теоремы следует, что в плоскости α существует прямая АВ, перпендикулярная прямой АН. Тогда из следствия к теореме 4.1 следует, что прямые АВ и СD не пересекаются. Проведем 
через точку А прямую АМ, отличную от прямой АВ, и пусть АМ – внутренний луч Ð НАВ (в противном случае надо рассматривать внутренний луч угла НАС), тогда Ð НАМ < Ð НАВ, поэтому Ð АНD + Ð НАМ < 2 d. Из этого по пятому постулату получаем, что прямые АМ и СD пересекаются. Следовательно, верна аксиома параллельности (Евклида). ■
|
|
Теорема. Пятый постулат Евклида эквивалентен утверждению: «Сумма углов треугольника равна 2d»
Доказательство.