Из (2) видно, что проводник обладает большой электроемкостью, если он обладает большими линейными размерами. Так, проводящий шар должен иметь большой радиус R. В технике же часто требуются устройства, которые при небольших линейных размерах и небольших приложенных напряжениях, могли бы накапливать большой электрический заряд, то есть обладать большой электроемкостью. Причем, электроемкость таких устройств не должна зависеть от расположения окружающих тел. Такие устройства называются конденсаторами. Если к заряженному проводнику поднести другой незаряженный проводник, то в результате электрической индукции на ближайшей к заряженному проводнику поверхности незаряженного проводника появится свободный заряд, разноименный с зарядом заряженного проводника, что приведет к уменьшению потенциала результирующего поля вблизи поверхности заряженного проводника (по принципу суперпозиции полей), а, следовательно, согласно (1), к увеличению его электроемкости. Следовательно, система из двух проводников будет обладать большей электроемкостью, чем один из этих проводников. Но электроемкость системы из 2-х произвольно расположенных проводников произвольной формы будет зависеть от расположения окружающих тел, так как электрическое поле, созданное этими двумя проводниками, будет существовать не только в пространстве между ними, но и за их пределами и вызывать смещение свободных зарядов в окружающих их проводниках и связанных зарядов в диэлектрических телах, что по принципу суперпозиции приведет к изменению разности потенциалов результирующего поля между двумя проводниками, а значит и к изменению их электроемкости.
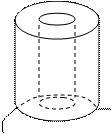
Конденсатор – это система таких двух проводников, служащая для накопления заряда, электроемкость которой не зависит от расположения окружающих тел. Оба проводника называются обкладками конденсатора. Они разделены слоем диэлектрика и имеют такую форму, чтобы создаваемое ими поле было сосредоточено в узком зазоре между ними и отсутствовало за их пределами. Тогда емкость конденсатора не будет зависеть от расположения окружающих тел. Электрическое поле будет существовать только между обкладками, если они представляют собой: 1) две плоские параллельные пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Причем, в каждом из этих случаев заряды на обкладках должны быть равными по модулю и противоположных знаков. Модуль заряда на каждой из обкладок называется зарядом конденсатора q.
+ - - - -
|
- -
- - -
|
|
|
|
- -
- - Рис. 3
|
|
- -
- -
|
|
- -
- - - -
Разность потенциалов между двумя точками поля еще называют электрическим напряжением между ними и обозначают U, то есть j 1- j 2 = U.
Тогда можно записать, что:
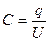(3а)
Конденсаторы бывают: 1) плоские – две плоские платины; 2) цилиндрические – два коаксиальных цилиндра; 3) сферические – две концентрические сферы (рис.3)
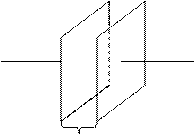
Рассчитаем электроемкость плоского конденсатора, площадь каждой пластины которого S, толщина диэлектрика или расстояние между пластина
ми (обкладками) – d, а диэлектрическая проницаемость - e.
+ ¾
 |
S
d
Рис.4
где U – напряжение между пластинами, Е – напряженность поля между ними. С другой стороны, эту напряженность можно записать по формуле напряженности поля, созданного двумя параллельными разноименно заряженными плоскостями с поверхностной плотностью заряда s
;
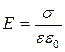здесь e - диэлектрическая проницаемость диэлектрика, находящегося между плоскостями.
Тогда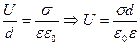 
, но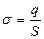 
,
где q – модуль заряда на пластине. Следовательно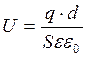 
.
Тогда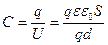 
, то есть 
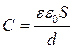(4)
Плавно изменяя площадь перекрытия пластин S, мы будем плавно изменять емкость плоского конденсатора. На этом основано действие конденсаторов переменной емкости.
Из (4) видно, что для дополнительного увеличения емкости плоского конденсатора надо увеличить площадь пластин и уменьшить толщину диэлектрика. Применение в качестве диэлектрика сегнетоэлектрики с аномально большой диэлектрической проницаемостью значительно увеличивают емкость конденсаторов.
Для варьирования емкости в широких пределах, имея набор конденсаторов постоянной емкости, используют параллельное и последовательное соединение, а также смешанное соединение конденсаторов в батареи.
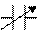При параллельном соединении конденсаторов по одной обкладке каждого конденсатора соединяются в один узел, а вторые обкладки каждого конденсатора соединяются в другой узел и оба узла подключаются к источнику напряжения (обозначение конденсаторов на схемах: - конденсатор постоянной емкости; - конденсатор переменной емкости).
Рассмотрим простейший случай – параллельное соединение двух конденсаторов (рис.5). Для параллельного соединения конденсаторов характерно следующее:
С 1
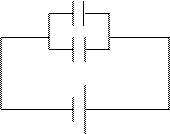- q 1 + q 2
А В
С 2
Рис.5
могут быть различными, то есть q 1 ¹ q 2, но общий заряд на полюсах батареи конденсаторов А и В будет равен сумме зарядов каждого конденсатора, то есть q = q1+q2
Из (3а) следует, что 
, где С пар – емкость батареи из параллельно соединенных конденсаторов. Тогда можно записать, что:
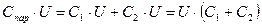
Следовательно,
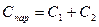
В общем случае параллельного соединения n конденсаторов
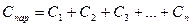(5)
то есть при параллельном соединении конденсаторов емкость всей батареи равна сумме емкостей отдельных конденсаторов, а значит она больше наибольшей из емкостей отдельных конденсаторов.
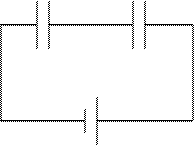
При последовательномсоединении конденсаторов одна обкладка первого конденсатора соединяется с любой обкладкой второго конденсатора, а свободная обкладка второго соединяется с обкладкой третьего конденсатора и т.д. Оставшиеся свободными обкладки первого и последнего конденсаторов подключаются к источнику напряжения.
C 1 C 2
- q + q -q +q
В 
А Д
Рис. 6
2) так как первая обкладка второго и вторая обкладка первого конденсаторов образуют единый проводник, то их потенциалы одинаковы и равны потенциалу произвольной точки В соединительного провода. Тогда получается, что:
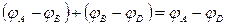или
,
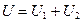то есть напряжение на полюсах батареи из последовательного соединения конденсаторов равно сумме напряжений на каждом конденсаторе. Из (За) следует, что:
,
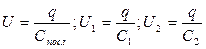где С посл – емкость батареи из последовательного соединения конденсаторов. Тогда можно записать, что:
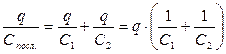
следовательно,
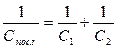(6)
в общем случае последовательного соединения n конденсаторов
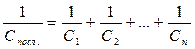, (6а)
то есть при последовательном соединении конденсаторов суммируется не сами емкости, а их обратные величины.
Из (6) следует, что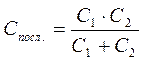 
Подстановка в эту формулу любых численных значений емкостей покажет, что при последовательном соединении конденсаторов емкость всей батареи меньше наименьшей из емкостей отдельных конденсаторов.
В любом смешанном соединении конденсаторов можно выделить участки из параллельного соединения конденсаторов, последовательно соединенные между собой, или наоборот.
В каждом из таких случаев, применяя формулу (5) и (6а), можно рассчитать емкость смешанного соединения конденсаторов.
Помимо емкости каждый конденсатор характеризуется пробивным напряжением - напряжением, при котором происходит пробой диэлектрика, конденсатор разряжается и выходит из строя. Пробивное напряжение зависит от формы обкладок, e, толщины диэлектрика.
Пробивное напряжение батареи из последовательного соединения конденсаторов равно сумме пробивных напряжений отдельных конденсаторов, а пробивное напряжение батареи из параллельно соединенных конденсаторов равно минимальному пробивному значению напряжения из имеющихся конденсаторов.
Энергия заряженного конденсатора определяется по формуле, аналогичной (3):
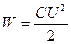. (7)
ЗАКЛЮЧЕНИЕ
Электростатика – это учение о стационарных зарядах и их взаимодействиях. Как мы уже видели, теорию можно строить на основе закона Кулона с использованием принципа суперпозиции. Однако это сложный путь. Более быстро в ряде задач можно достичь цели, используя теорему Гаусса. На основании этой теоремы нами рассмотрено поведение диэлектриков и проводников в электрическом поле и получены основные количественные соотношения.
Нами рассмотрены конденсаторы – необходимые элементы колебательных контуров, применяемые широко в устройствах автоматизации.
Разработал доцент каф. ТиЕНД Кустов Ал.И.
«___»________2020_г.