Федеральное государственное бюджетное образовательное учреждение
Высшего образования
«Воронежский государственный педагогический университет»
КАФЕДРА Технологических и естветственнонаучных дисциплин
УТВЕРЖДАЮ
Заведующий кафедрой ТиЕНД доцент Е. Чернышева
«» 2020 г.
Автор: канд. техн. наук, доцент Кустов А.И.
Дисциплина:
Прикладные вопросы физики в автоматизированных системах управления технологическими процессами
КАФЕДРАЛЬНЫЙ ТЕКСТ ЛЕКЦИИ №1-02
ВВВЕДЕНИЕ В КУРС. КОНДЕСАТОРЫ, КАК ЭЛЕМЕНТЫУСТРОЙСТВ АВТОМАТИЗАЦИИ..
«02 » сентября 2020г.
г. Воронеж-2020
ПЛАН занятия
Учебные вопросы
Вступительная часть
1. П роводники в электрическом поле и явление электрической индукции
2. Э лектроемкость проводника
3. К онденсаторы и их соединения
Заключительная часть
Вступительная часть
Прикладные вопросы физики в автоматизированных системах управления технологическими процессами – эта дисциплина многопланова и многогранна.При этом она непосредственно связана с нашим профилем – с технологиями. Нам известно, что практически все технологии опираются на фундаментальные знания, полученные, прежде всего в физике. Поэтому, в рамках изучаемой дисциплины сплелись воедино несколько современных направлений развития науки и производства. Прежде всего – опора на фундаментальные закономерности; в торое – демонстрация практического использования знаний о материальном мире, их прикладная значимость; и третье – получение технологических достижений с применением информационных технологий.
Сосредоточимся на тех областях физики, которые преуспели в прикладных вопросах, или близки к этому. Прежде всего, это такие разделы как механика, гидро- и аэродинамика, электричество и магнетизм, физика твердого тела и др. В рамках изучаемой нами дисциплины первостепенное значение имеют электромагнитные взаимодействия и компьютерные, информационные технологии (так как позволяют создавать широкий спектр датчиков, с помощью которых можно управлять различными процессами, при этом доводя автоматизацию до 100%).
|
|
Итак, наш курс достаточно ограничен по времени, поэтому сосредоточимся на главном – рассмотрим принципы создания и функционирования устройств управления, определим алгоритмы расчета параметров таких систем. Прежде всего изучим резисторы (используемые в термометр ах сопротивлений), термопары, магнитные датчики (например, Холла), конденсаторы различных типов, колебательные контуры и проч.
1. Проводники в электрическом поле и явление электрической индукции
К проводникам относятся вещества, в которых концентрация свободных зарядов очень велика, поэтому они хорошо проводят электрический ток.
Внесение незаряженного проводника в электрическое поле приводит к перемещению свободных зарядов: положительных – по полю, а отрицательных – против поля. В металлических проводниках свободными заряженными частицами являются свободные (валентные) электроны, которые смещаются против внешнего поля, создавая избыток электронов, а значит отрицательный заряд, на одной поверхности проводника, и их недостаток, а значит положительный заряд, на противоположной поверхности).
|
|
Рис. 1
Заряды, появившиеся на двух противоположных поверхностях проводника при его внесении во внешнее электрическое поле, называются индуцированными.
Таким образом, незаряженный проводник разрывает часть линий напряженности внешнего электрического поля: они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных.
Явление смещения свободных зарядов в проводнике и образование в нем внутреннего электрического поля под воздействием внешнего электрического поля называется электрической индукцией.
Так как индуцированные заряды располагаются только на поверхности проводника, то при наличии полости внутри него электрическое поле там отсутствует. На этом основана электростатическая защита – экранирование тел, например, измерительных приборов, от внешнего электростатического поля.
Таким образом, условия равновесия индуцированных зарядов на проводнике следующие:
1. Напряженность поля внутри проводника должна равняться нулю, а значит, потенциал во всех точках внутри проводника и на его поверхности должен быть одинаковым.
Из первого условия вытекает второе:
2. Поверхность проводника во внешнем поле должна быть эквипотенциальной, а значит, линии напряженности за пределами проводника должны быть перпендикулярны к его поверхности.
3. Все индуцированные заряды располагаются на поверхности проводника.
|
|
|
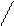
+ s DS
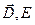
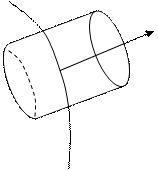
Рис. 2
Так как поле внутри проводника отсутствует, то поток вектора Ф D
через замкнутую цилиндрическую поверхность определяется только потоком сквозь его наружное основание:
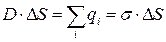, то есть 
.
.
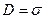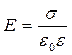Так как s - поверхностная плотность смещенных зарядов, то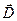 
называют вектором электрического смещения. Отсюда можно сделать вывод, что при данном потенциале поверхностная плотность зарядов определяется кривизной поверхности. Особенно велика, бывает s, а, следовательно,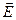 
и 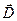на остриях, даже может происходить ионизация воздуха, возникает ощутимое движение газа, называемое электрическим ветром, при этом заряд проводника уменьшается, как бы стекает с острия (или, наоборот, натекает с других тел).
ЭЛЕКТРОЕМКОСТЬ ПРОВОДНИКА
Известно, что потенциал электрического поля, созданного точечным заряженным телом в вакууме, определяется по формуле:
,
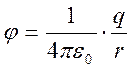где r – расстояние от данной точки поля до точечного заряженного тела. Видно, что потенциал данной точки поля пропорционален заряду точечного заряженного тела. Опыт показывает, что для заряженного проводника любой формы потенциал электрического поля, созданного этим проводником, в любой точке, в том числе в непосредственной близости от поверхности проводника, пропорционален заряду проводника. Значит и заряд заряженного проводника пропорционален потенциалу его поверхности, то есть q ~ j или
.
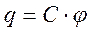Скалярная физическая величина С называется электроемкостью проводника.
Следовательно, электроемкость проводника определяется по формуле: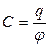 
; (1)
Из (1) следует, что электроемкость проводника численно равна заряду, который надо сообщить незаряженному проводнику, чтобы потенциал его поверхности стал равным единице потенциала или электроемкость проводника также численно равна заряду, который надо сообщить заряженному проводнику, чтобы увеличить потенциал его поверхности на единицу потенциала.
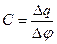(1¢)
Таким образом, электроемкость проводника характеризует его способность накапливать электрический заряд. Единица измерения электроемкости в системе СИ: [С]СИ = 1Ф = 1Кл/1В (Фарад). Проводнику емкостью 1Ф надо сообщить заряд в 1 Кл, чтобы увеличить потенциал его поверхности на 1В.
С, как коэффициент пропорциональности между q и j, не зависит ни от заряда проводника q, ни от потенциала его поверхности j. Но емкость проводника зависит от его размеров и формы и от диэлектрической проницаемости среды, в которой находится проводник. Например, потенциал поверхности сферического (шарообразного) проводника радиусом R в соответствии с формулой для потенциала электрического поля точечного заряда определяется по формуле:
,
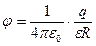где e - диэлектрическая проницаемость окружающей среды. Тогда в соответствии с (1) емкость шара будет определяться по формуле:
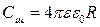, (2)
то есть действительно будет зависеть от размеров шара (от его радиуса R) и от диэлектрической проницаемости e окружающей среды.
Из (2) следует, что единица измерения электрической постоянной e 0 в системе СИ – Ф/м.
Так как проводник емкостью в 1Ф при потенциале его поверхности всего лишь в 1В успевает накопить заряд в 1Кл, а это очень большой заряд, то это значит, что 1Ф – это очень большая емкость. На практике обычно применяются гораздо меньшие емкости, и используются гораздо меньшие единицы измерения емкости. Чаще всего это 1мкФ = 10-6Ф (микрофарад) и 1пФ = 10-12Ф (пикофарад). Из (2) следует, что емкостью в 1Ф обладал бы шар, находящийся в вакууме и имеющий радиус R =9×106 км, то есть примерно в 1400 раз больше радиуса Земли (емкость Земли С з » 0,7мФ (милифарад); 1мФ = 10-3Ф).
Итак, проводник обладает способностью накапливать электрический заряд, следовательно, заряженный проводник обладает энергией – это потенциальная энергия электрического поля вокруг этого проводника
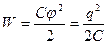. (3)