Во всех странах имеются метеорологические службы, которые занимаются регистрацией и распространением метеосводок, в том числе и данных о направлении и силе ветра. Как правило, параметры ветра регистрируются на одной стандартной высоте – 10 м. Поэтому эти данные можно использовать лишь для грубой оценки ветроэнергетических ресурсов изучаемого района, но их чаще всего недостаточно для принятия конкретных технических решений, например, для выбора оптимальной конструкции ВЭУ. Для этого, как правило, необходимы более детальные наблюдения в большом числе точек местности и на разных высотах в различные месяцы года. Результаты этих наблюдений можно сравнить со стандартными метеоданными и в дальнейшем учитывать корреляцию между ними.
Скорость ветра подразделяется метеослужбами по исторически сложившейся шкале Бофорта, в основе которой лежат визуальные наблюдения [17, 32].
Скорость ветра при стандартных метрологических измерениях определяется осреднением показателей анемометра, находящегося на 10-метровой высоте. Эти измерения могут повторяться каждый час, но обычно они проводятся значительно реже, поэтому по ним трудно судить о флуктуациях скорости ветра и его направлених, что необходимо для расчета характеристик ветроустановок.
Скорости ветра на разных высотах различны, поэтому различны и воздействия ветра на ветроколесо, расположенное на разной высоте. На рис. 9.15 показано распределение скорости ветра по высоте 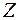 с уровня земли до высоты примерно 100 м.
с уровня земли до высоты примерно 100 м.
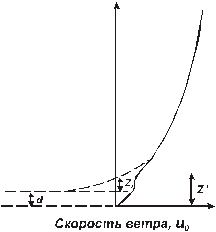
Рисунок 9.15 – Зависимость скорости 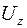 ветра над поверхностью земли (
ветра над поверхностью земли (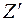 – высота местных препятствий)
– высота местных препятствий)
На поверхности земли (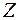 =0) скорость ветра всегда равна нулю.
=0) скорость ветра всегда равна нулю.
Затем до высоты, примерно равной высоте, расположенных в данном месте различных препятствий (зданий, деревьев и т.д.), скорость ветра увеличивается очень сложным образом, при этом его направление может изменяться практически случайно. Выше этой области зависимость скорости ветра от высоты имеет вид:
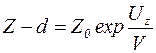 . (9.39)
. (9.39)
или в явном виде относительно 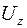 :
:
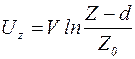 , (9.40)
, (9.40)
где 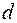 – смещение нулевого уровня, значение которого несколько меньше высоты местных препятствий;
– смещение нулевого уровня, значение которого несколько меньше высоты местных препятствий;  – высота препятствий относительно смещенного нулевого уровня;
– высота препятствий относительно смещенного нулевого уровня; 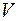 – характерная скорость.
– характерная скорость.
Опыт показывает, что наилучшим местом для размещения ВЭУ является гладкая, куполообразная, ничем не затененная возвышенность. Вообще желательно, чтобы ветроустановка в радиусе нескольких сот метров была окружена полями или водной поверхностью.
Как правило, головки ветроустановок находятся от 5 до 50 м. Для определения скорости 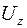 на этих высотах часто используют зависимость, в которую входит значение стандартной скорости ветра
на этих высотах часто используют зависимость, в которую входит значение стандартной скорости ветра 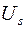 , измеренное на высоте 10 м. Она имеет вид:
, измеренное на высоте 10 м. Она имеет вид:
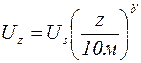 . (9.41)
. (9.41)
Как показывает опыт, для открытых мест параметр 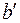 =0,14. Чем меньше значение параметра
=0,14. Чем меньше значение параметра 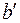 , тем меньше будут различаться нагрузки, испытываемые лопастью ветроколеса в нижнем и верхнем положениях. Очевидно, что значения параметра
, тем меньше будут различаться нагрузки, испытываемые лопастью ветроколеса в нижнем и верхнем положениях. Очевидно, что значения параметра 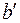 различны в разное время года, и даже в течение одного дня, поэтому формулой (40) следует пользоваться очень осторожно и осмотрительно, особенно для высоты
различны в разное время года, и даже в течение одного дня, поэтому формулой (40) следует пользоваться очень осторожно и осмотрительно, особенно для высоты 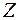 >50 м.
>50 м.
В большинстве задач ветроэнергетики гораздо важнее знать не суммарное количество энергии, которое может выработать ветроагрегат, например, за год, а ту мощность, которую она может обеспечивать постоянно. При сильном ветре, большем, например, 12 м/с, ветроустановки вырабатывают вполне достаточно электроэнергии, поэтому часто в этих условиях её приходится сбрасывать или запасать.
Основные трудности возникают в периоды длительного затишья или слабого ветра.
Поэтому для ветроэнергетики является законом считать районы со средней скоростью более 8 м/с – очень хорошими. Но независимо от этого во всех случаях требуется тщательный выбор параметров ветроустановки применительно к местным метеоусловиям.
Для детального аналитического расчета режимов работы ветроустановки следует предварительно провести или математическую обработку массивов экспериментальных данных о скорости ветра в течение года, или, пользуясь определенной теоретической функцией распределения 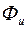 для вероятности скорости ветра, найти аналитическое выражение, соответствующее экспериментальным данным.
для вероятности скорости ветра, найти аналитическое выражение, соответствующее экспериментальным данным.
Второй случай более предпочтителен, так как, во-первых, резко сократилось бы необходимое количество замеров скорости ветра и, во-вторых, появилась бы возможность аналитического расчета характеристик ВЭУ.
Величина 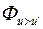 – это часть времени года, в течение которого будут ветра со скоростью большей
– это часть времени года, в течение которого будут ветра со скоростью большей 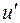 . Эта величина безразмерная. Часто пользуются величиной
. Эта величина безразмерная. Часто пользуются величиной 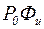 – это мощность ветрового потока единичного сечения (удельная мощность) Величину
– это мощность ветрового потока единичного сечения (удельная мощность) Величину 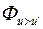 можно описать так:
можно описать так:
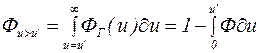 . (9.42)
. (9.42)
Откуда следует, что
 . (9.43)
. (9.43)
График 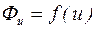 изображен на рис. 9.16.
изображен на рис. 9.16.
Практика показывает, что очень хорошо функцию 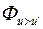 аппроксимирует так называемая функция Вейбулла (см. рис. 9.17), записанная в виде:
аппроксимирует так называемая функция Вейбулла (см. рис. 9.17), записанная в виде:
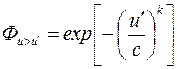 , (44)
, (44)
или
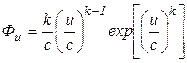 , (45)
, (45)
где 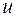 – скорость ветра,
– скорость ветра, 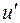 – величина скорости меньше заданной.
– величина скорости меньше заданной.
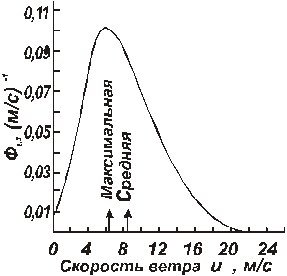
Рисунок 9.16 – Функция распределения скорости ветра

Рисунок 9.17 – Функция вероятности скорости ветра, большей 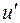 (для плотности вероятности, вычисленной по рисунку 9.16)
(для плотности вероятности, вычисленной по рисунку 9.16)
Более точное соответствие экспериментальным данным получается при значениях параметра 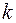 =1,8-2,3 и параметра
=1,8-2,3 и параметра 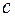 , близкого к значению средней скорости ветра
, близкого к значению средней скорости ветра 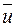 .
.
Выражение (9.45) можно ещё более упростить – свести к одному параметрическому так называемому распределению Рэлея Х–квадратичному распределению), полагая 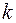 =2:
=2:
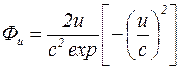 . (9.46)
. (9.46)
Выразим среднее значение скорости ветра 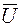 через функцию:
через функцию:
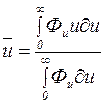 . (9.47)
. (9.47)
Подставляя в (9.47), например, функцию Вейбулла, получаем:
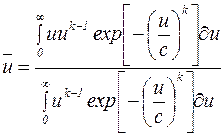 . (9.48)
. (9.48)
Обозначим  , тогда
, тогда  , и уравнение (9.48) примет вид:
, и уравнение (9.48) примет вид:
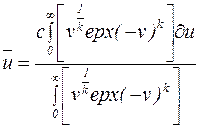 . (9.49)
. (9.49)
В этом выражении знаменатель равен единице, а числитель – стандартная функция, именуемая гамма-функцией, или факториалом, обозначаемая как
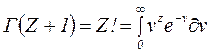 . (9.50)
. (9.50)
Так как аргумент в гамма-функции принято обозначать 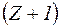 , а не
, а не 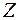 , то (9.50) следует представить в виде:
, то (9.50) следует представить в виде:
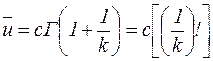 . (9.51)
. (9.51)
Используя известные свойства гамма-функции, нетрудно вычислить среднее значение переменной 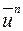 , где
, где 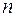 – целое или дробное число. В общем случае для функции Вейбулла имеем:
– целое или дробное число. В общем случае для функции Вейбулла имеем:
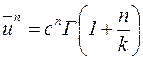 . (9.52)
. (9.52)
При 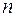 =3 имеем
=3 имеем
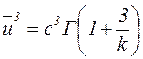 . (9.53)
. (9.53)
Откуда можно получить выражение для энергии ветра.
Значения параметров 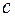 и
и 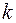 определятся из аппроксимации конкретных данных метеонаблюдений распределением Вейбулла. Но если, например, известны
определятся из аппроксимации конкретных данных метеонаблюдений распределением Вейбулла. Но если, например, известны 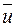 и
и  , то параметры
, то параметры 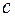 и
и 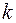 определяются системой уравнений (9.51) и (9.53). Современные методы первичной обработки метеоинформации позволят достаточно просто определить
определяются системой уравнений (9.51) и (9.53). Современные методы первичной обработки метеоинформации позволят достаточно просто определить 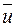 и
и  , не обращаясь к результатам многочисленных отдельных измерений.
, не обращаясь к результатам многочисленных отдельных измерений.