ЗАДАНИЕ К УРОКУ №42,43
Дата 03.11.2020 Группа МР-111
Дисциплина/МДК/УП: Физика
Темы уроков: Твердые тела
План занятия:
1. Посмотрите материал https://resh.edu.ru/subject/lesson/3741/start/78608/ Урок 22. Жидкости и твердые тела класс 10
2. Прочитайте учебник Мякишев «Физика» углубленный уровень глава 12 параграф 73-74
3. Дополнительно можно использовать учебник Дмитриев «Физика для технических специальностей » глава 8 параграф 8.1-8.5
4. На оценку «3»
Написать в тетрадь глоссарий (смотри ниже). Срок сегодня до 17.00
На оценку «4»
На сайте РЭШ пройти тренировочное задание 5 из 14 https://resh.edu.ru/subject/lesson/3741/train/78614/, скриншоты отправить мне в личку ВК
Срок сегодня
На оценку «5»
На сайте РЭШ пройти тренировочное задание 5 из 14 https://resh.edu.ru/subject/lesson/3741/train/78614/, скриншоты отправить мне в личку ВК до …….. и привести 5 примеров поверхностного натяжения жидкости.
Срок сегодня
Желаю плодотворной работы!
Конспект урока
Физика, 10 класс
Урок 22. Жидкости и твёрдые тела
Перечень вопросов, рассматриваемых на уроке:
Модели твердого тела и жидкости;
Поверхностное натяжение жидкости;
Смачивание;
Капиллярность
Глоссарий по теме
Кристаллическая решетка– это упорядоченное расположение атомов или молекул в определенных точках пространства.
Коэффициент поверхностного натяжения жидкости – это величина равная работе, которую необходимо совершить, чтобы увеличить площадь поверхности на единицу.
Угол смачивания – это угол, образованный поверхностью жидкости с поверхностью твердого тела, откладываемый внутри жидкости.
Основная и дополнительная литература по теме урока:
1. А.В. Грачев, В.А. Погожев, А.М. Салецкий и др. Физика. 10 класс. - М. «Вентана-Граф», 2014.
2. А. П. Рымкевич. Сборник задач по физике. 10-11 класс. - М. «Дрофа»,2009.
3. Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н. Ракина, К.С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 178-184
4. Я.И. Перельман Занимательная физика. - М.: “Наука”, 1991.- С. 51 - 54
5. А.К. Кикоин О силах поверхностного натяжения. Квант. – 1983. - №12 – С. 27 - 28
Основное содержание урока
Каковы главные особенности в строении жидкости и твердого тела, которые отражаются на различии их физических свойств. Главными признаками при сравнении жидкости и твердого тела являются упорядоченность в расположении частиц и расстояния между ними.
В разных условиях одни и те же вещества могут находиться в разных агрегатных состояниях: газообразном, жидком и твердом состояниях. При этом одни и те же молекулы одного и того же вещества по-разному движутся и взаимодействуют друг с другом.
По современным представлениям в жидкости молекулы колеблются относительно некоторой точки равновесия и время от времени совершают скачкообразное движение, покидая своих соседей. Такое движение молекул объясняет известное свойство жидкости, как текучесть, способность жидкости принимать форму сосуда, в котором она содержится. При соблюдается некоторый «ближний» порядок в расположении молекул.
В модели кристаллов молекулы совершают только колебательные движения около точек, которые называются узлами кристаллической решетки.
Кристаллическая решетка – это упорядоченное расположение упорядоченное расположение определенных точках пространства.
Таким образом в расположении частиц твердого тела соблюдается не только ближний, но и «дальний» порядок, распространяющийся по всем направлениям кристалла.
Фаза – это равновесное состояние вещества, отличающееся по своим физическим свойствам от других состояний. Переход от одной фазы вещества к другой сопровождается изменением внутренней энергии системы.
Одно и то же вещество в твёрдом и жидком состояниях может иметь по нескольку различных фаз.
Твердые тела характеризуются высокой механической прочностью.
По сравнению с твердыми телами жидкости характеризуются большой подвижностью молекул, и как следствие, меньшей упорядоченностью молекул и их слабым взаимодействием.
Кроме кристаллов к твёрдым телам относя аморфные и жидкие кристаллы.
Аморфные тела – это твёрдые тела, в которых соблюдается только ближний порядок в расположении частиц и отсутствует определенная температура плавления. ряд явлений, присущих только жидкому состоянию вещества.
Среди свойств жидкости особую роль играют такие свойства, как поверхностное натяжение и смачивание. Молекулы поверхностного слоя жидкости находятся в условиях, отличающихся от условий существования молекул внутри её объёма.
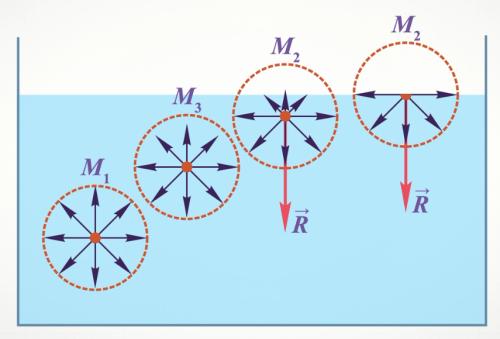
На каждую молекулу поверхностного слоя действует результирующая сила со стороны остальных молекул, направленная вовнутрь жидкости. Таким образом, жидкость как будто находится под натянутой пленкой.
Поэтому, если жидкость оказывается без стенок сосуда и в условиях невесомости, то она приобретает форму с мини минимальной площадью поверхности, т.е. шара.
Среди свойств жидкости особую роль играют такие свойства, как поверхностное натяжение и смачивание.
При увеличении площади поверхности жидкости на некоторую величину внешними силами совершается работа.
Отношение этой работы к изменению площади поверхности называется коэффициентом поверхностного натяжения
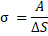
На рисунке изображена проволочная рамка с одной подвижной стороной, на которую «натянута» мыльная плёнка.

Прикладывая внешнюю силу можно растягивать эту пленку, совершая работу против силы поверхностного натяжения.
Из формулы для работы внешних сил найдём
 ,
,
откуда 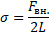
Учитывая тот факт, что у мыльной пленки две поверхности натяжения,
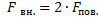
получим ещё одну формулу для коэффициента поверхностного натяжения жидкости

Коэффициент поверхностного натяжения равен силе, действующей со стороны поверхности жидкости на единицу длины контура (границы) поверхности и стремящейся уменьшить площадь этой поверхности.
Рассмотрим границу между жидкой и твердой фазой на примере жидкости в цилиндрическом сосуде.
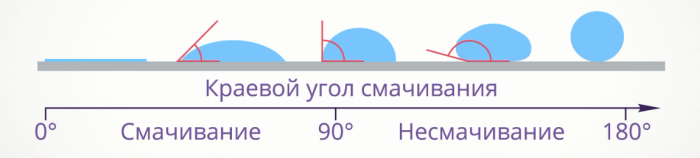
Твердое тело – стенка сосуда. Влиянием газовой фазы пренебрегаем. Если молекулы жидкости, находящиеся вблизи границы Т-Ж(твёрдое тело – жидкость) на ее свободной поверхности, притягиваются к твердому телу сильнее, чем к жидкости, то они «вытягивается» из жидкости в сторону твердого тела, т.е. увеличивается площадь границы Т-Ж. И наоборот. Если силы притяжения молекул из граничной области к жидкой фазе больше, чем к твердой, то площадь границы Т-Ж стремится к уменьшению. Получающийся на границе угол края жидкости к твердому телу называется углом смачивания.
Если этот угол меньше 900, говорят имеет место смачивание; если – больше 900, несмачивание. Если угол равен 00, то такое явление называется растеканием (говоря другими словами - очень хорошее смачивание).
Поверхностное натяжение и смачивание является причиной такого явления как капиллярность - необычного поведения жидкостей в тонких трубках (капиллярах) и узких щелях.
В зависимости от смачивания или несмачивания жидкость в капиллярах может иметь высоту подъёма больше или меньше уровня свободной поверхности жидкости в большом сосуде. Формула высоты уровня жидкости в капилляре для случая идеального смачивания имеет вид
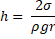
Разбор тренировочных заданий
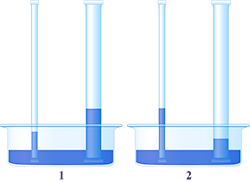
1. На рисунках изображены разные моменты опыта по измерению высоты поднятия жидкости в капилляре.
Расположите рисунки в правильной временной последовательности.

Решение. В опыте капилляр опускается в жидкость, и жидкость поднимается до некоторого предельного уровня. Учитывая эту последовательность, расставим картинки

2. Ответьте на вопросы:
1.Найдите радиус капилляра (мм), если известно, что

2.Чему равен угол смачивания, если жидкость растекается по поверхности твердого тела?
3.Чему равен угол смачивания, если жидкость не смачивает твердое тело?
4.Приведите номер рисунка, верно отражающего явление капиллярности
5. выберите номер капилляра, в котором жидкость поднимется выше? Если
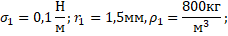

Решение.
1.Из формулы для высоты поднятия жидкости в капилляре в случае хорошего смачивания имеем
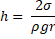
Отсюда получим выражение для радиуса

вычислим r = (2*0,1)/(800*10*0,025) =0,001 м = 1 мм;
2.Если жидкость растекается, угол смачивания равен нулю (00);
3.Есмли жидкость не смачивает твёрдое тело, угол смачивания равен 1800;
4.Если в одну и ту же жидкость опустить два капилляра из одного и того же материала, смачивающегося данной жидкостью, но разного радиуса, то чем меньше радиус капилляра, тем больше высота уровня жидкости в капилляре. Верный вариант – 2;
5. Считаем по формуле:
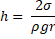
h1 = (2*0,1)/(800*10*0,0015) =0,01666 м =16,7 мм;
h2 = (2*0,05)/(1000*10*0,0005) =0,02 м = 20 мм
Ответ:1; 0; 180; 2; 2.