Определение1. Тройка некомпланарных векторов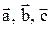 
называется правой (левой) если, находясь внутри телесного угла, образованного приведенными к общему началу векторами 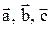и от него к 
, човершающимся против часовой стрелки (по часовой стрелке)
 |
Тройка правая Тройка левая
Определение 2. Векторным произведением вектора на вектор 
называется вектор 
, длина и направление которого определяются условиями:
1. 
, где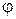 
- угол между 
.
2. 
.
3. 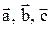- правая тройка векторов.
Свойства векторного произведения
1. 
(свойство антиперестановочности сомножителей);
2. 
(распределительное относительно суммы векторов);
3. 
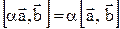(сочетательное относиельно числового множителя);
4. 
(равенство нулю векторного произведения означает коллинеарность векторов);
5. 
, т. е. момент сил равен векторному произведению силы на плечо.
Если вектор 
, то 
.
Определение 3. Смешанным произведением 
трех векторов называется число, определяемое следующим образом: 
. Если векторы заданы своими координатами: 
, то
~ 
.
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности векторов 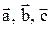является равенство = 0.
2. Объем параллелепипеда, построенного на векторах 
: 
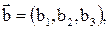
Примеры решения задач
Задача 1. Найти координаты векторного произведения 
, если 
, 
.
Решение. Найдем 
и 
. Векторное произведение, по определению, равно 
.
Задача 2. Силы 
и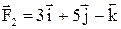 
приложены к точке 
. Вычислить величину момента равнодействующей этих сил 
относительно точки 
.
Решение. Найдем силу и плечо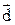 
: 
. Момент
сил 
вычисляется по формуле
, а его модуль 
.
Задача 3. Даны координаты вершин параллелепипеда: 
. Найти объем параллелепипеда, его высоту, опущенную из вершины С, угол между вектором AD и гранью, в которой лежат векторы АВ и АС.
Решение. По определению, объем параллелепипеда равен смешанному произведению векторов, на которых он построен. Найдем эти векторы:
.
Объем этого параллелепипеда 
.
С другой стороны, объем параллелепипеда 
, 
- это площадь параллелограмма: 
.
, тогда высота 
.
Угол между вектором и гранью 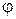найдем по формуле
.
так как вектор 
перпендикулярен грани, в которой лежат векторы 
. Угол между этим вектором и вектором 
находим по известной формуле
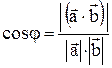. Очевидно, что искомый угол 
.
Итак: 
.
Задача 4. Проверить, лежат ли в одной плоскости точки 
, 
. Найти линейную зависимость вектора 
, если это возможно.
Решение. Найдем три вектора: 
.
.
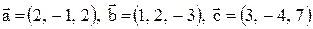Три вектора лежат в одной плоскости, если они компланарны, т. е. их смешанное произведение равно нулю: 
. Следовательно, эти три вектора линей-
но зависимы. Найдем линейную зависимость 
от 
.
.
Решая эту систему, получим 
, т.е. 
.
Задачи
1. 
. Вычислить: а) 
; б) 
;
в) 
.
2. 
. Вычислить площадь треугольника, построенного на векторах 
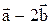и 
.
3. Заданы векторы 
. Найти координаты векторов:
а) 
б) 
; в) 
.
4. Вычислить площадь треугольника с вершинами 
.
5. В треугольнике с вершинами 
, 
и 
найти высоту 
.
6. Найти вектор 
, если векторы 
имеют следующие координаты:
.
7. Сила 
приложена к точке 
. Определить момент этой силы относительно точки 
.
8. Установить, образуют ли векторы 
базис в множестве всех вектров, если а) 
; б)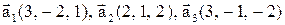 
.
9. Вычислить объем тетраэдра ОАВС, если 
.
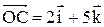10. В тетраэдре с вершинами в точках 
и
вычислить высоту 
.
11. Проверить, компланарны ли данные векторы:
а) 
;
б) 
.
12. Доказать, что четыре точки 
лежат в одной плоскости.
13. Найти координаты четвертой вершины тетраэдра ABCD, если известно, что она лежит на оси Oy, а объем тетраэдра равен V:
а)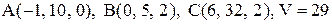 
;
б) 
.
Домашнее задание
1. Упростить выражение 
.
2. Найти площадь параллелограмма, построенного на векторах 
и 
, где 
- единичные векторы, угол между которыми равен 
.
3. Даны векторы 
. Найти вектор
.
4. Дан треугольник с вершинами 
. Найти его площадь.
5. Даны силы 
, приложенные к точке 
. Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки 
.
6. Вычислить объем параллелепипеда, построенного на векторах:
1) 
, где 
- взаимно перпендикулярные орты;
2) 
.
7. Доказать, что точки 
лежат в одной
плоскости.
8. Даны вершины тетраэдра 
. Найти длину высоты, опущенной из вершины О на грань АВС.
9. Векторы 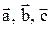, образующие правую тройку, взаимно перпендикулярны. Зная,
что 
, вычислить 
.
10. Вектор перпендикулярен к векторам , угол между равен 
. Зная, что 
, вычислить .
11. Даны векторы 
. Вычислить 
.
12. Установить, компланарны ли векторы 
, если
1) 
;
2) 
;
3) 
.
13. Доказать, что точки 
лежат в одной плоскости.
14. Вычислить объем тетраэдра, вершины которого находятся в точках 
.
15. Даны вершины тетраэдра 
. Найти его высоту, опущенную из вершины D.
16. Объем тетраэдра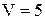 
, три его вершины находятся в точках 
. Найти координаты четвертой вершины D, если известно, что она лежит на оси 
.
Ответы к задачам
1) 
. 2) 
. 3) (-3, 5, 7), (-6, 10, 14), (-12, 20, 28).
4) 
. 5) 5. 6) (-20, 7, -11). 8) Нет, да. 9) 17/2. 10) 
. 11) Да, нет.
13) (0, 0, 0), (0, 1, 0).
Ответы к домашнему заданию
1) 
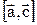. 2) 
. 3) 
. 4) 
. 5) 
. 6) 0. 8) 11.
9) 24. 10) 
. 11) -7. 12) Да, нет, да. 14) 3. 15) 11. 16) (0, 8, 0), (0, -7, 0).
 |