ПРАКТИЧЕСКИЕ
ЗАНЯТИЯ
«ВЕКТОРНАЯ АЛГЕБРА »
 Занятие 1
Занятие 1
Линейные операции над векторами. Линейная зависимость векторов
Определение 1. Геометрическим вектором, или просто вектором, называется направленный отрезок.
Будем обозначать вектор либо как направленный отрезок символом  , где точки А и В - начало и конец данного вектора, либо
, где точки А и В - начало и конец данного вектора, либо  . Начало вектора называют точкой его приложения.
. Начало вектора называют точкой его приложения.
Определение 2. Вектор называется нулевым, если начало и конец егосовпадают.
Нулевой вектор не имеет определенного направления и имеет длину, равную нулю. Это позволяет при записи отождествлять нулевой вектор с вещественным числом нуль.
Определение 3. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.
Определение 4. Три вектора называются компланарными, если они лежат в одной плоскости.
Определение 5. Два вектора называются равными, если они коллиннеарны, имеют одинаковую длину и одинаковое направление.
Все нулевые векторы считаются равными.
Определение 6. Суммой 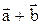 двух векторов
двух векторов  и
и  называется вектор, идущий из начала вектора
называется вектор, идущий из начала вектора  в конец вектора
в конец вектора  при условии, что вектор
при условии, что вектор  приложен к концу вектора
приложен к концу вектора  .
.
Определение 7. Разностью  вектора
вектора  и вектора
и вектора  называется такой вектор
называется такой вектор  , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор  .
.
Определение 8. Произведением 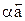 вектора
вектора  на действительное число
на действительное число  называется вектор
называется вектор  , коллинеарный вектору
, коллинеарный вектору  , имеющий длину, равную
, имеющий длину, равную  , и имеющий направление, совпадающее с направлением вектора
, и имеющий направление, совпадающее с направлением вектора  при
при 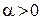 и противоположное направлению вектора
и противоположное направлению вектора  при
при 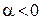 .
.
Обозначим буквами  основания перпендикуляров, опущенных на ось
основания перпендикуляров, опущенных на ось  из точек А и В соответственно.
из точек А и В соответственно.
 В
В

А



Определение 9. Проекцией вектора  на ось
на ось  называется величина
называется величина 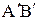
направленного отрезка  оси
оси  и обозначается
и обозначается  .
. 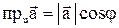 , где
, где 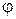 - угол между вектором
- угол между вектором  и осью
и осью  .
.
Любой вектор  может быть разложен по декартову прямоугольному базису
может быть разложен по декартову прямоугольному базису  :
:  .
.
Числа  - называется декартовыми прямоугольными координатами вектора
- называется декартовыми прямоугольными координатами вектора  . Обозначим буквами
. Обозначим буквами 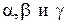 углы наклона вектора
углы наклона вектора  к осям координат;
к осям координат;  называются направляющими косинусами вектора
называются направляющими косинусами вектора  .
.
Длина вектора через его координаты имеет вид  .
.
Направляющие косинусы вектора вычисляются по формулам:
 ;
;  ;
;  ,
,
откуда следует  .
.
Определение 10. Ортом вектора  называется вектор
называется вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям:
1)  коллинеарен вектору
коллинеарен вектору  ,
,
2)  .
.
Координатами орта вектора являются направляющие косинуса.
Если два вектора  заданы в декартовых прямоугольных координат
заданы в декартовых прямоугольных координат  ,
,  ,то
,то 
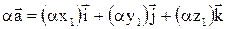 .
.
Условие коллинеарности векторов имеет вид  .
.
Примеры решения задач
Задача 1. В равнобедренной трапеции ОАСВ угол  ,
, 
 ,
,
 - середина сторон ВС и АС. Выразить векторы
- середина сторон ВС и АС. Выразить векторы  через
через  - единичные векторы направлений
- единичные векторы направлений  .
.
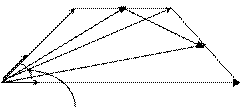 В М С
В М С
 N
N
O A


Решение.  . Так как
. Так как  . Найдем
. Найдем
вектор  . Из треугольника ОСА
. Из треугольника ОСА 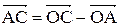 , а так как
, а так как  , а
, а
 , вектор
, вектор  . Найдем
. Найдем  из треуголь-
из треуголь-
ника ONC  , а так как
, а так как  ,
,  ,
,  .
.
Из треугольника OMN  .
.
Задача 2. Даны векторы  и
и  , приложены к общей точке. Найти орт биссектрисы угла между
, приложены к общей точке. Найти орт биссектрисы угла между  .
.
Решение. Диагональ четырехугольника совпадает с биссектрисой, если этот четырехугольник – ромб (квадрат). Найдя  , получим угол с одинаковыми по длине сторонами, равными единице. Таким образом, вектор
, получим угол с одинаковыми по длине сторонами, равными единице. Таким образом, вектор  направлен по биссектрисе угла между
направлен по биссектрисе угла между  .
.
 ,
, 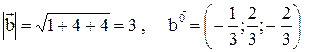 ,
,
 .
.
Найдем длину вектора 
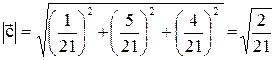 , тогда орт биссектрисы равен
, тогда орт биссектрисы равен  .
.
Задача 3. Разложить вектор  по трем некомпланарным векторам:
по трем некомпланарным векторам: 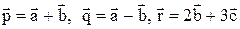 .
.
Решение.  .
. 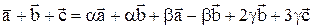 .
.
Приравняем коэффициенты справа и слева:
 тогда
тогда 
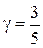 и
и 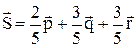 .
.
Задачи
1. Построить вектор 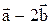 по данным векторам
по данным векторам  .
.
2. В треугольнике ОАВ даны векторы 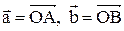 . Найти векторы
. Найти векторы 
 , где М – середина стороны АВ.
, где М – середина стороны АВ.
3. Пользуясь параллелограммом, построенным на векторах  , проверить на чертеже справедливость тождества
, проверить на чертеже справедливость тождества  .
.
4. В равнобочной трапеции АВСD известно нижнее основание  , боковая
, боковая
сторона  и угол между ними
и угол между ними  . Разложить по
. Разложить по  все векторы,
все векторы,
составляющие остальные стороны и диагонали трапеции.
5. Даны модуль вектора  и углы
и углы 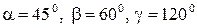 . Вычислить проекции вектора
. Вычислить проекции вектора  на координатные оси.
на координатные оси.
6. Вычислить направляющие косинусы вектора  .
.
7. Вектор составляет с осями ОХ и OZ углы  и
и  . Какой угол он
. Какой угол он
составляет с осью OY?
8. Даны  . Найти
. Найти  .
.
9. Даны 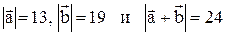 . Вычислить
. Вычислить  .
.
10. Векторы 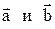 образуют угол
образуют угол  , причем
, причем  . Определить
. Определить  .
.
11. Даны четыре вектора:  . Определить разложение каждого из этих четырех векторов, принимая в качестве базиса три остальных.
. Определить разложение каждого из этих четырех векторов, принимая в качестве базиса три остальных.
12. Даны точки  . Проверить, что векторы
. Проверить, что векторы  коллинеарны; установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну сторону или в противоположные.
коллинеарны; установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну сторону или в противоположные.
13. Найти орт вектора  .
.
14. Два вектора 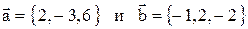 приложены к одной точке. Определить координаты вектора
приложены к одной точке. Определить координаты вектора  , направленного по биссектрисе угла между векторами
, направленного по биссектрисе угла между векторами  и
и  , при условии, что
, при условии, что  .
.
15. Исследовать на линейную зависимость систему векторов 
 .
.
16. Доказать, что векторы 

 линейно независимы и разложить по ним вектор
линейно независимы и разложить по ним вектор  .
.
Домашнее задание
1. Определить точку N, с которой совпадает конец вектора 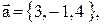 если его
если его
начало совпадает с точкой М (1, 2,- 3).
2. Вектор  составляет с осями координат острые углы
составляет с осями координат острые углы  при
при  и
и  . Найти его координаты, если
. Найти его координаты, если  .
.
3. Векторы  образуют угол
образуют угол 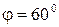 , причем
, причем 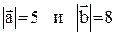 . Определить
. Определить  .
.
4. Точка О является центром масс треугольника АВС. Доказать, что  .
.
5. Три силы  , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей
, приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей  , если известно, что
, если известно, что  .
.
6. Найти орт вектора  .
.
7. Векторы 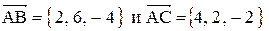 совпадают со сторонами треугольника АВС. Определить координаты векторов, приложенных к вершинам треугольника и совпадающих с его медианами АМ, BN, CP.
совпадают со сторонами треугольника АВС. Определить координаты векторов, приложенных к вершинам треугольника и совпадающих с его медианами АМ, BN, CP.
8. Даны вершины треугольника:  . Вычислить длину биссектрисы его внутреннего угла при вершине А.
. Вычислить длину биссектрисы его внутреннего угла при вершине А.
9. Зная векторы, служащие сторонами треугольника  , найти векторы, соответственно коллинеарные биссектрисам углов этого треугольника.
, найти векторы, соответственно коллинеарные биссектрисам углов этого треугольника.
10. На плоскости даны четыре точки:  . Определить разложение векторов
. Определить разложение векторов  , принимая в качестве базиса векторы
, принимая в качестве базиса векторы  .
.
11. Даны три вектора:  . Найти разложение вектора
. Найти разложение вектора  по базису
по базису  .
.
Ответы к задачам
4.  .
.
5. 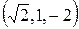 . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9. 22. 10.  .
.
11. 

 .
.
13. 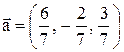 . 14.
. 14.  . 16.
. 16.  .
.
Ответы к домашнему заданию
1.  . 2.
. 2.  . 3.
. 3.  .
.
5.  . 6.
. 6.  . 7.
. 7.  .
.
8. 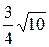 .
.
9. 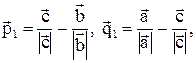
 ,
,
где  имеют направление внутренних углов А, В и С
имеют направление внутренних углов А, В и С 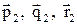 имеют направления биссектрис одноименных внешних углов треугольника.
имеют направления биссектрис одноименных внешних углов треугольника.
10. 

 . 11.
. 11.  .
.
 Занятие 2
Занятие 2
Скалярное произведение векторов
 Определение. Скалярным произведением ненулевых векторов
Определение. Скалярным произведением ненулевых векторов  называется число
называется число  ;
;  .
.
Свойства скалярного произведения:
1)  (переместительное);
(переместительное);
2)  (сочетательное относительно числового множителя);
(сочетательное относительно числового множителя);
3)  (распределительное относительно суммы векторов).
(распределительное относительно суммы векторов).
Если  , то
, то 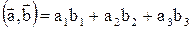 ,
,  .
.
Условие перпендикулярности векторов 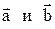 :
:  .
.
Длина вектора  :
: 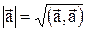 .
.
Физический смысл скалярного поизведения: если вектор  представляет силу, точка приложения которой перемещается из начала в конец вектора
представляет силу, точка приложения которой перемещается из начала в конец вектора 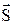 , то работа А этой силы определяется равенством
, то работа А этой силы определяется равенством  .
.
Примеры решения задач
 Задача 1. Определить длины диагоналей параллелограмма, построенного на векторах
Задача 1. Определить длины диагоналей параллелограмма, построенного на векторах  и
и  , где
, где  таковы, что
таковы, что  .
.
Решение. Диагонали параллелограмма есть векторы 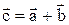 и
и  . Вычислим длину вектора
. Вычислим длину вектора  :
:  .
.
Аналогично вычисляется длина вектора 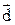 .
.
Задача 2. Найдите вектор  , коллинеарный вектору
, коллинеарный вектору  и удовлетворяющий условию
и удовлетворяющий условию 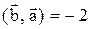 .
.
Решение. Обозначим вектор 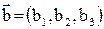 , тогда из условий задачи
, тогда из условий задачи
 или
или 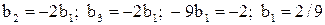 ,
,
тогда  . Итак:
. Итак:  .
.
Задача 3. Найти проекцию вектора 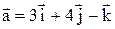 на направление вектора
на направление вектора  .
.
Решение.  . По формуле проекции вектора на ось будет иметь место равенство
. По формуле проекции вектора на ось будет иметь место равенство
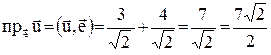 .
.
Задача 4. Даны векторы:  .
.
 Проверить, есть ли среди них коллинеарные. Найти
Проверить, есть ли среди них коллинеарные. Найти  .
.
Решение. Условие коллинеарности имеет вид  . Этому условию удовлетворяют векторы
. Этому условию удовлетворяют векторы  . Следовательно, они коллинеарны. Найдем длины
. Следовательно, они коллинеарны. Найдем длины
векторов  :
:  .
.
Угол между векторами определяется по формуле  .
.

 Тогда
Тогда  ,
,  .
.
Используя формулу  , получим
, получим 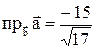 .
.
Задача 5. На материальную точку действуют силы 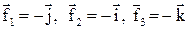 . Найти работу равнодействующей этих сил
. Найти работу равнодействующей этих сил  при перемещении точки из положения
при перемещении точки из положения  в положение
в положение  .
.
Решение. Найдем силу  и вектор перемещения
и вектор перемещения  .
.  , тогда искомая работа
, тогда искомая работа  .
.
Задачи
1. Векторы  взаимно перпендикулярны, а вектор
взаимно перпендикулярны, а вектор  образует с ними углы
образует с ними углы  . Зная, что
. Зная, что  , найти: 1)
, найти: 1)  ; 2)
; 2) 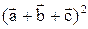 .
.
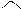 2. Вычислить длину диагоналей параллелограмма, построенного на векторах
2. Вычислить длину диагоналей параллелограмма, построенного на векторах  , если известно, что
, если известно, что  .
.
3. Доказать, что вектор  перпендикулярен к вектору
перпендикулярен к вектору  .
.
 4. Зная, что
4. Зная, что 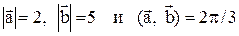 , определить, при каком значении коэффициента
, определить, при каком значении коэффициента  векторы
векторы 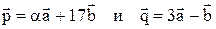 окажутся перпендикулярными.
окажутся перпендикулярными.
5. Даны вершины четырехугольника: 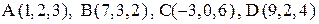 . Доказать, что его диагонали взаимно перпендикулярны.
. Доказать, что его диагонали взаимно перпендикулярны.
6. Найти острый угол между диагоналями параллелограмма, построенного на векторах 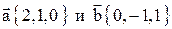 .
.
7. Даны силы  . Найти работу их равнодействующей при перемещении точки из начала координат в точку
. Найти работу их равнодействующей при перемещении точки из начала координат в точку  .
.
8. Даны вершины треугольника:  . Найти проекцию вектора
. Найти проекцию вектора  на вектор
на вектор  .
.
9. Найти вектор  , перпендикулярный векторам
, перпендикулярный векторам  , если известно, что его проекция на вектор
, если известно, что его проекция на вектор  равна единице.
равна единице.
10. Сила, определяемая вектором 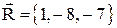 , разложена по трем направлениям, одно из которых задано вектором
, разложена по трем направлениям, одно из которых задано вектором  . Найти составляющую силы
. Найти составляющую силы  в направлении вектора
в направлении вектора  .
.
11. Даны вершины треугольника: 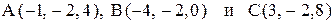 . Найти его внутренний угол при вершине А и внешний угол при вершине В.
. Найти его внутренний угол при вершине А и внешний угол при вершине В.
12. Даны три последовательные вершины параллелограмма:  . Найти его четвертую вершину D и угол между векторами
. Найти его четвертую вершину D и угол между векторами  .
.
13. На оси  найти точку, равноудаленную от точек
найти точку, равноудаленную от точек  .
.
14. Доказать, что треугольник с вершинами 
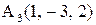 прямоугольный.
прямоугольный.
Домашнее задание
1. Вычислить скалярное произведение двух векторов 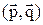 , зная их разложение по трем единичным взаимно перпендикулярным векторам
, зная их разложение по трем единичным взаимно перпендикулярным векторам 
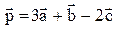 ;
;  .
.
2. Найти длину вектора  , зная, что
, зная, что  – взаимно перпендику-
– взаимно перпендику-
лярные орты.
3. Векторы 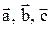 попарно образуют друг с другом углы, каждый из которых равен
попарно образуют друг с другом углы, каждый из которых равен  . Зная, что
. Зная, что  , определить модуль вектора
, определить модуль вектора  .
.
4. Доказать, что вектор 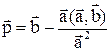 перпендикулярен к вектору
перпендикулярен к вектору  .
.
5. Даны векторы 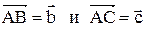 , совпадающие со сторонами треугольника АВС. Найти разложение вектора, приложенного к вершине В этого треугольника и совпадающего с его высотой BD по базису
, совпадающие со сторонами треугольника АВС. Найти разложение вектора, приложенного к вершине В этого треугольника и совпадающего с его высотой BD по базису  .
.
6. Вычислить угол между векторами  , где
, где  - единичные взаимно перпендикулярные векторы.
- единичные взаимно перпендикулярные векторы.
7. Даны силы 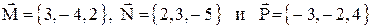 , приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения
, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения 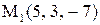 в положение
в положение  .
.
8. Даны вершины треугольника  . Определить его внутренний угол при вершине В.
. Определить его внутренний угол при вершине В.
9. Вычислив внутренние углы треугольника с вершинами 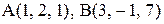 ,
,  , убедиться, что этот треугольник равнобедренный.
, убедиться, что этот треугольник равнобедренный.
10. Найти вектор  , зная, что он перпендикулярен векторам
, зная, что он перпендикулярен векторам  и
и 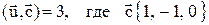 .
.
11. Найти вектор  , коллинеарный вектору
, коллинеарный вектору  и удовлетворяющий условию
и удовлетворяющий условию  , где
, где 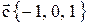 .
.
12. Вычислить проекцию вектора 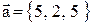 на ось вектора
на ось вектора  .
.
13. Даны векторы  . Вычислить
. Вычислить 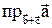 .
.
14. Даны точки 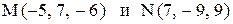 . Вычислить проекцию вектора
. Вычислить проекцию вектора 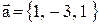 на ось вектора
на ось вектора  .
.
Ответы к задачам
1) -7, 13. 2) 15,  . 4)
. 4)  . 6)
. 6)  . 7) 2. 8) -1/3.
. 7) 2. 8) -1/3.
9) 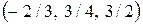 . 10)
. 10)  . 11)
. 11)  .
.
12) 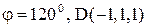 . 13)
. 13) 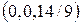 .
.
Ответы к домашнему заданию
1) 9. 2) 5. 3) 10. 5)  . 6)
. 6) 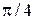 . 7) 13. 8)
. 7) 13. 8) 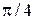 .
.
10)  . 12) 6. 13) 5. 14) 3.
. 12) 6. 13) 5. 14) 3.
Занятие 3