Векторным произведением вектора

Векторная алгебра

1. Вектор (направленный отрезок) — упорядоченная пара точек. Первая называется началом вектора, вторая концом.Закрепленный вектор с началом в точке A и концом в точке B обозначается .Вектор, у которого начало и конец совпадает, называется нулевым и обозначается 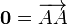. Длина вектора (модуль или абсолютная величина) — расстояние между его началом и концом, обозначается .

Операции над векторами

Пусть в линейном пространстве выбран базис и в нём представлены вектора вектора , , тогда суммой векторов будет называется следующий вектор: .
Пусть есть число λ, тогда произведением вектора 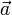на число λ будет называться следующий вектор: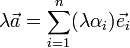
Два ненулевых вектора 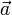и 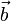называются коллинеарными, если .

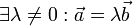Свойства

Сложение векторов коммутативно: .

Сложение векторов ассоциативно: .

Прибавление нулевого вектора к любому не меняет последнего: 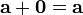. Очевидно, .

Для любого вектора существует вектор такой, что или .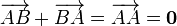

Проекция вектора на ось

Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора.

Теорема 1

.

Проекция вектора а на ось равна:

Доказательство:

Х – проекция вектора а на ось,

Теорема доказана.

Теорема 2.

Проекция суммы векторов на ось равна сумме проекций слагаемых векторов на ту же ось.

Доказательство:

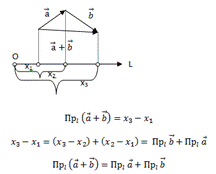
Теорема 3.

Если вектор а умножить на число, то и его проекция на ось умножиться на это число.

Доказательство:

Если λ>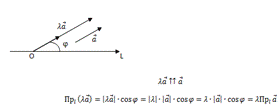

Если λ<0

 

Теорема доказана.

3. Базисом на плоскости (в пространстве)-называется упорядоченная пара (тройка) неколлинеарных (некомпланарных) векторов. Любой вектор однозначным образом раскладывается по базису. Коэффициенты разложения называются координатами этого вектора относительно данного базиса. Векторы образуют базис в декартовом координатном пространстве Oxyz.

Разложение вектора по базису.

Определение. Пусть 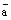– произвольный вектор, 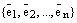– произвольная система векторов. Если выполняется равенство

, (1)

то говорят, что вектор 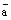представлен в виде линейной комбинации данной системы векторов. Если данная система векторов 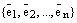является базисом векторного пространства, то равенство (1) называется разложением вектора 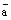по базису 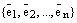. Коэффициенты линейной комбинации называются в этом случае координатами вектора 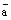относительно базиса .

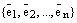Скалярное произведение векторов

Скалярное произведение — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. a*b={a_x*b_x + a_y*b_y + a_z* b_z}

Если хотя бы один из векторов равен нулю, то скалярное произведение равно нулю.

Скалярное произведение в координатах

Если 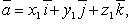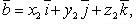то

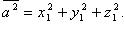
Ортогональность двух векторов

Для того, чтобы два вектора были ортогональны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю, то есть (х, у)=0.

(х, у)=0 – условие ортогональности двух векторов

Векторным произведением вектора

C = A x B

1) Вектор С действует вдоль прямой перпендикулярой A и B = > C перпендик. A и B

2) С по длине равен площади параллелограмма С = S = |A| * |B| sin α

3) A, B, C –правая тройка A x B = -B x A