Задачу по оптимизации маршрута легко представить в виде сети, так как каждое перемещение из пункта отправки в пункт прибытия является направленным и представляет собой дугу, а сами пункты в таком случае, представляют вершины сети (сетью называется ориентированный граф, в котором существует лишь одна вершина, не имеющая входящих дуг, и лишь одна вершина, не имеющая выходящих дуг).
Карта, приведенная на рисунке 25, по своей сути сама является сетью, но сеть удобнее представлять в упрощенном виде, не соблюдая масштабов и пропорций, а указывая только связи между вершинами:
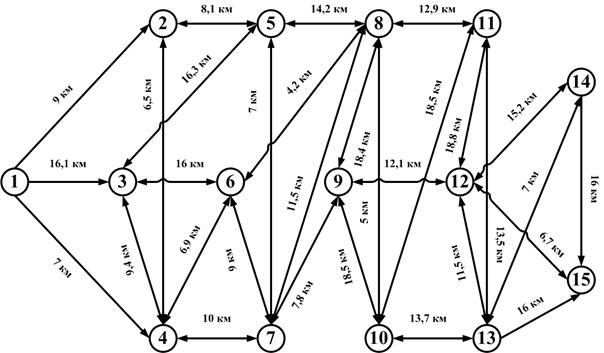
Рисунок 32. Сеть поставленной задачи по оптимизации маршрута
Пункты пронумерованы в порядке «слева-направо, сверху-вниз». Стрелки на концах дуг указывают направления, в которых может происходить перемещение транспорта из одного пункта в другой. В целях упрощения расчетов будем считать, что перемещение обратно в пункт 1 из пунктов 2, 3 и 4 невозможно (так как не соответствует требованиям задачи); также невозможен выезд из пункта 15 (так как цель уже достигнута). Рядом с каждой дугой указана ее характеристика (в данном случае – расстояние между пунктами в километрах).
Для решения задач оптимизации маршрута разработаны несколько методов: метод полного перебора вариантов, метод ветвей и границ, метод Дейкстры и т.д. Но для выполнения вручную они требуют значительных затрат времени, а для автоматизированного решения – специальных программных средств.
Практически любую сетевую задачу оптимизации маршрута движения можно решить с помощью методов линейного программирования. В качестве переменных в данной задаче принимаются передвижения по дугам.
Например, передвижение из пункта 2 в пункт 4 будет обозначено переменной X2-4, а переезд из пункта 4 в пункт 2 – переменной X2-4. Таким образом, дуге с двумя стрелками на концах будут соответствовать две переменные, дуге с одной стрелкой – одна переменная. Переменные в этой задаче – булевого (двоичного) типа, они принимают значение 0, если перемещение по дуге состоялось, и значение 1, если перемещения не было.
Выезд транспортного средства из пункта 1 может быть описан в следующем виде:
 .
.
Так как переменная булева, то лишь одна из трех переменных примет значение 1. Например, если X1-3 = 1, то транспортное средство переместится из пункта 1 в пункт 3.
Проезд через остальные пункты будет обеспечен уравнениями следующего вида (пример ‑ уравнение для пятого пункта):
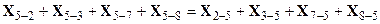 .
.
По этому условию количество выездов из 5 пункта (во 2, 3, 7 или 8 пункт) равно количеству въездов в него (из 2, 3, 7 или 8 пункта). В левой, как и в правой части уравнения, лишь одна переменная может принять значение 1. Например, X5-8 = 1 и X3-5 = 1, таким образом, в пятый пункт транспорт прибыл из третьего, а уедет – в восьмой. Для простоты реализации этих уравнений в «Поиске решения» перенесем переменные из правой части в левую:
 .
.
Достижение конечного (пятнадцатого) пункта будет реализовано следующим уравнением:
 .
.
Целевая функция данной задачи представляет собой пройденное расстояние, находимое как сумма произведений расстояний между пунктами на количество переездов между ними (0 или 1):
 .
.
В структурном виде данная задача записывается следующим образом:

где n – количество вершин сети (или номер конечного пункта назначения), Сi-j – вес дуги i-j (расстояние от i-го пункта до j-го пункта).
Сетевая модель в матричной форме приведена в таблице 36.
Таблица 21. Модель по оптимизации маршрута движения в табличной (матричной форме)
| № | 1_2 | 1_3 | 1_4 | 2_4 | 2_5 | 3_4 | 3_5 | 3_6 | 4_2 | 4_3 | 4_6 | 4_7 | 5_2 | 5_3 | 5_7 | 5_8 | 6_3 | 6_4 | 6_7 | 6_8 | 7_4 | 7_5 | 7_6 | 7_8 | 7_9 | 8_5 | 8_6 | 8_7 | 8_9 |
| -1 | -1 | -1 | |||||||||||||||||||||||||||
| -1 | -1 | -1 | -1 | ||||||||||||||||||||||||||
| -1 | -1 | -1 | -1 | -1 | |||||||||||||||||||||||||
| -1 | -1 | -1 | -1 | ||||||||||||||||||||||||||
| -1 | -1 | -1 | -1 | ||||||||||||||||||||||||||
| -1 | -1 | -1 | -1 | ||||||||||||||||||||||||||
| -1 | -1 | -1 | |||||||||||||||||||||||||||
| -1 | -1 | ||||||||||||||||||||||||||||
| Z | 9,0 | 16,1 | 7,0 | 6,5 | 8,1 | 9,4 | 16,3 | 16,0 | 6,5 | 9,4 | 6,9 | 10,0 | 8,1 | 16,3 | 7,0 | 14,2 | 16,0 | 6,9 | 9,0 | 4,2 | 10,0 | 7,0 | 9,0 | 11,5 | 7,8 | 14,2 | 4,2 | 11,5 | 18,4 |
Продолжение таблицы 21
| № | 8_10 | 8_11 | 9_7 | 9_8 | 9_10 | 9_12 | 10_8 | 10_9 | 10_11 | 10_13 | 11_8 | 11_10 | 11_12 | 11_13 | 12_9 | 12_11 | 12_13 | 12_14 | 12_15 | 13_10 | 13_11 | 13_12 | 13_14 | 13_15 | 14_12 | 14_13 | 14_15 | Bi | |
| = | |||||||||||||||||||||||||||||
| = | |||||||||||||||||||||||||||||
| = | |||||||||||||||||||||||||||||
| = | |||||||||||||||||||||||||||||
| = | |||||||||||||||||||||||||||||
| = | |||||||||||||||||||||||||||||
| -1 | = | ||||||||||||||||||||||||||||
| -1 | -1 | -1 | = | ||||||||||||||||||||||||||
| -1 | -1 | = | |||||||||||||||||||||||||||
| -1 | -1 | -1 | -1 | = | |||||||||||||||||||||||||
| -1 | -1 | -1 | -1 | = | |||||||||||||||||||||||||
| -1 | -1 | -1 | -1 | = | |||||||||||||||||||||||||
| -1 | -1 | -1 | -1 | = | |||||||||||||||||||||||||
| -1 | -1 | = | |||||||||||||||||||||||||||
| -1 | -1 | -1 | = | -1 | |||||||||||||||||||||||||
| Z | 5,0 | 12,9 | 7,8 | 18,4 | 18,5 | 12,1 | 5,0 | 18,5 | 18,5 | 13,7 | 12,9 | 18,5 | 18,8 | 13,5 | 12,1 | 18,8 | 11,5 | 15,2 | 6,7 | 13,7 | 13,5 | 11,5 | 7,0 | 16,0 | 15,2 | 7,0 | 16,0 | ||