Практическая работа №3
«Расчёт неразветвленной цепи переменного тока»
Цель: закрепить навыки расчета неразветвленных цепей переменного тока, построение векторных диаграмм.
Средства обучения: методические указания по выполнению практической работы, калькулятор, карандаш, шариковая ручка, линейка, транспортир.
Краткие теоретические сведения.
Решение задачи этой группы требует знания учебного материала по теме «неразветвленные цепи переменного тока» и предоставления об особенностях расчета таких цепей. Для пояснения методики расчета подобных схем рассмотрим пример. На рисунке 1 изображена схема неразветвленной цепи.

Рисунок 1- Схема неразветвленной цепи
Все элементы электрической цепи обладают сопротивлением, которые делятся на:
активное - резистор, R, Ом;
реактивное - конденсатор, емкостное XC, Ом;
катушка индуктивности, индуктивное ХL, Ом.
полное - Z, Ом.
Сопротивления определяются по формулам
R = ρ· 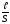 ; (1)
; (1)
XC = 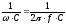 ; (2)
; (2)
ХL = 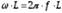 ; (3)
; (3)
Z = 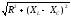 (4)
(4)
где ρ - удельное сопротивление проводника, 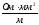 ; ᶩ -длина проводника, м; S – сечение проводника, мм2, ω – циклическая частота, рад/м; L – индуктивность, Гн; f – линейная частота, Гц; C – емкость,Ф.
; ᶩ -длина проводника, м; S – сечение проводника, мм2, ω – циклическая частота, рад/м; L – индуктивность, Гн; f – линейная частота, Гц; C – емкость,Ф.
Основными параметрами, характеризующими электрическую цепь, являются сила тока I, А, напряжение U, В, связанные законом Ома
I = 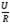 (5)
(5)
Коэффициент мощности или угол сдвига фаз между векторами тока и напряжения определяется
Сosφ = 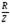 (5.6)
(5.6)
Активную P, реактивную Q и полную S мощности цепи определяют соответственно по формулам
Р = I·U·Cosφ, Вт; (7)
Q = I·U·Sinφ, ВАр; (8)
S = 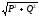 = I·U, В·А (9)
= I·U, В·А (9)
Методика построения топографической векторной диаграммы напряжений неразветвленной цепи.
1. Определяем значения реактивных сопротивлений ХL, XC для элементов L1, L2, C1, C2 по формулам (2),(3)
XC1 = 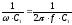 ; XC2 =
; XC2 = 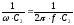 ;
;
ХL1 = 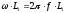 ; ХL2 =
; ХL2 = 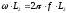 ,
,
где ω – циклическая или угловая частота, рад/с;
f – линейная частота, f =50Гц;
L – индуктивность катушки, Гн;
С – емкость конденсатора, Ф.
2. Определяем значения падения напряжения UR, UL, UC, В, на элементах цепи R1, R2, L1, L2, C1, C2 согласно закона Ома (5.5)
UR1 = I0· R1; UR2 = I0· R2;
UL1 = I0· ХL1; UL2 = I0· ХL2;
UC1 = I0· XC1 ; UC2 = I0· XC2.
3. Выбираем масштаб векторной диаграммы значений тока и напряжения.
4. По полученным значениям падения напряжения строимтопографическую векторную диаграмму напряжений, основываясь на следующих принципах:
а) вектор тока I0 откладывают по горизонтальной прямой, так как его начальная фаза равна нулю;
б) вектор UR совпадает по фазе с вектором I;
в) вектор UL откладывают вертикально вверх, так как его фаза равна плюс π/2;
г) вектор UС откладывают вертикально вниз, так как его фаза равна минус π/2;
д) результирующий вектор напряжения U как геометрическая сумма всех составляющих:
U = UR1 + UR2 + UC1 + UC2 + UL1 + UL2.
5. На построенной диаграмме графически определяем угол сдвига фаз между вектором тока I0 и результирующим вектором напряжения U -  φ.
φ.
6. Определяем результирующие активные R и реактивные ХL, XC, полное сопротивления Z цепи по формулам
R = R1 + R2; ХL = ХL1 + ХL2; XC = XC1 + XC2;
Z = 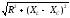 .
.
7. Определяем угол сдвига фаз между векторами тока и напряжения
Сosφ = 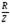 ; Sinφ =
; Sinφ = 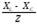 .
.
+8. Определяем активную UR, реактивную UL,UC и полную U составляющую напряжения.
UR = UR1 + UR2; UL = UL1 + UL2; UC = UC1 + UC2;
U = 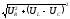 .
.
9. Определяем активную, реактивную и полную мощности неразветвленной цепи
Р1 = I0·U·Cosφ, Вт;
Q1 = I0·U·Sinφ, ВАр;
S1 = 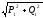 = I1·U1, В·А
= I1·U1, В·А
Пусть по цепи протекает ток с начальной фазой φ, равной нулю 𝑖 = 𝐼𝑚 ∙ 𝑠𝑖𝑛𝜔𝑡. Переходя к действующим значениям, можно записать векторную сумму напряжений:
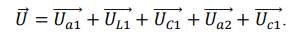
Эта сумма лежим в основе построения векторной диаграммы. Таким образом, напряжение цепи равно геометрической сумме напряжений на всех участках этой цепи. Из векторной диаграммы следует (рисунок 2)
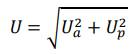
где 𝑈𝑎 - активное напряжение цепи, равное арифметической сумме напряжений на активных участках цепи: 𝑈𝑎 = 𝑈𝑎1 + 𝑈𝑎2;
𝑈𝑝 - реактивное напряжение цепи, равное алгебраической сумме напряжений на реактивных участках цепи: 𝑈𝑝 = 𝑈𝐿1 − 𝑈𝐶1 − 𝑈𝐶2
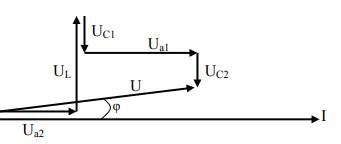
Рисунок 2 – Векторная диаграмма
Те же рассуждения можно отнести и к сопротивлениям:
- полное сопротивление цепи: 𝑍 = √𝑟2 + 𝑥2;
- активное сопротивление цепи: 𝑟 = 𝑟1 + 𝑟2;
- реактивное сопротивление цепи: 𝑥 = 𝑥𝐿1 − 𝑥𝐶1 − 𝑥𝐶2.
После построения векторной диаграммы можно с помощью транспортира и линейки сравнить угол сдвига фаз φ и длину вектора напряжения с расчетными значениями.
Задание.
1. Начертить схему согласно исходных данных (таблица 1).
2. Найти I, UR,UL, UC, P, Q, S.
3. Построить векторную диаграмму напряжений.
4. Написать выражение для мгновенного значения u.
Пример выполнения расчёта.
Дано:
L1=20мГн
R1=22 Ом
C1=25мкФ
U=200 В
f=50Гц
Задание.
1. Начертить схему согласно исходных данных (таблица 1).
2. Найти I, UR,UL, UC, P, Q, S.
3. Построить векторную диаграмму напряжений.
4. Написать выражение для мгновенного значения u.
Решение.
1.Начертить схему с1

2. Найдем сопротивления всех элементов цепи:
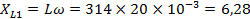 Ом
Ом
где 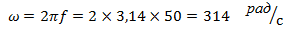
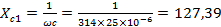 Ом
Ом
3. Найдем полное сопротивление всей цепи: 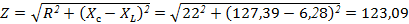 Ом
Ом
4. Найдем полный ток:
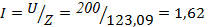 А
А
5. Найдем активную мощность:
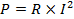
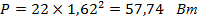
4. Найдем реактивную мощность:
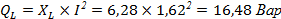
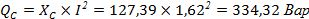
5. Найдем полную мощность:
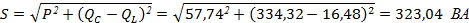
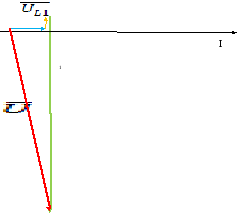
6. Построим векторную диаграмму напряжений.
Для того чтобы построить векторную диаграмму напряжений найдем напряжения на каждом элементе цепи:
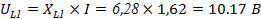
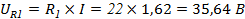
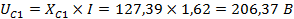
Масштаб: возьмём в 1см=10 В.
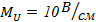 =1см:
=1см:
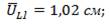
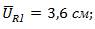
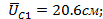
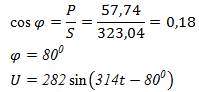
Содержание отчета.
1. Название и цель практической работы.
2. Схема и исходные данные согласно своему варианту.
4. Расчеты пункта задания 2.
4. Векторная диаграмма напряжений в масштабе.
5. Ответы на контрольные вопросы.
Контрольные вопросы.
1.Что означают выражения Z, XL, Xc, R и как они записываются?
2.Дайте понятие − активной Р, реактивной Q и полной S мощности.
3.Что показывает векторная диаграмма напряжений?
Таблица 1 – Варианты индивидуальных заданий
| № варианта | L, м Гн | С, мкФ | R, Ом | f, Гц | U, В |