Векторная алгебра.
В природе имеют место векторные и скалярные величины. Скалярная величина характеризуется только числом (температура, время, масса). Векторные величины характеризуются величиной и направлением в пространстве.
Вектором называется отрезок, имеющий определенную длину и определенное направление в пространстве.


B Обозначение АВ, a.
a

A |AB|, | a| − длина вектора.
Два вектора называются равными, если 1) их длины равны, 2) векторы параллельны имеют одинаковое направление в пространстве.


 a = b. B
a = b. B
 a C
a C
b

 A AB ≠ CD
A AB ≠ CD
D
 | |||
 | |||
AB = a, CD = - a
Сложение векторов.




 Суммой двух векторов называется третий вектор, исходящий из их общего начала, и являющийся диагональю параллелограмма, построенного на слагаемых векторах как на сторонах. c = a + b
Суммой двух векторов называется третий вектор, исходящий из их общего начала, и являющийся диагональю параллелограмма, построенного на слагаемых векторах как на сторонах. c = a + b

 B
B
C AC = b, a + AC = c

 b c
b c
b c
 O a A b
O a A b
a
правило треугольника


 Правило треугольника распространяется на сложение большего числа векторов.
Правило треугольника распространяется на сложение большего числа векторов.


 c
c
a+b + cd
ba + b + c = 
a
В конце предыдущего вектора помещается начало последующего. Вектор, замыкающий эту ломаную, есть вектор суммы. Начало его совпадает с началом первого вектора, а конец с концом последнего вектора.
Свойства суммы векторов.
1. a + b = b + a − коммутативность.
2. (a + b) + c = a + (b + c) − сочетательность (ассоциативность).
Разность векторов.
Векторc называется разностью векторов c = a – b, если b + c = a.
 |
b c = a - b
a
Умножение вектора на число.
Произведением вектора a на число λ называется вектор, длина которого равна
| λ|∙|c|, параллельный вектору a и направленный в ту же сторону, что и вектор a, если λ > 0, и в противоположную, если λ < 0.
 .
.

 a
a
λ a (λ > 0)
λ a (λ < 0)
1. (λ + μ) a = λ a + μ a,
2. λ(μ a) = (λμ )∙a.
3. 






 λ(a + b) = λ a + λ b
λ(a + b) = λ a + λ b
 λ b
λ b
λ cc = a + b
b c (-1) a = -a.
a λ a
Проекция вектора на ось.
 Рассмотрим вектор АВ и ось l. ПустьА1 – проекция точки А на ось l,
Рассмотрим вектор АВ и ось l. ПустьА1 – проекция точки А на ось l,
В1 – проекция точки В на ось l.


 Проекцией вектора АВ на ось l называется число, равное длине вектора А1В1, расположенного на оси, взятой со знаком (+), если направление вектора А1В1совпадает с направлением оси и со знаком (−), если эти направления противоположны.
Проекцией вектора АВ на ось l называется число, равное длине вектора А1В1, расположенного на оси, взятой со знаком (+), если направление вектора А1В1совпадает с направлением оси и со знаком (−), если эти направления противоположны.


















 B B
B B

 A A
A A


 B1 A1 l
B1 A1 l

 A1 B1 l
A1 B1 l
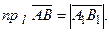

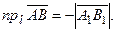
Теоремы о проекциях.
1. 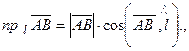
-
 Проекция суммы векторов равна сумме проекций.
Проекция суммы векторов равна сумме проекций.


 a b
a b

 c=a+b
c=a+b
 |  |
A1 A2 A3
Координаты вектора.


 Рассмотрим три единичных взаимно перпендикулярных вектора i, j, k, образующих правую тройку.
Рассмотрим три единичных взаимно перпендикулярных вектора i, j, k, образующих правую тройку.
kk




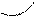 j i
j i
j
i
правая тройка левая тройка.
|i| = |j| = |k| = 1. Единичные векторы i, j, k называются ортами.
В направлении каждого из этих векторов проведем оси. Получим пространственную систему координат.
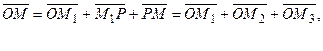
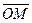 = X i + Y j + Z k (*)
= X i + Y j + Z k (*)


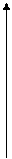


z

 M3
M3




 М
М
 |
k
j M2 y
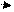


 i
i
 M 1
M 1


 P
P
x
X, Y, Z – проекции вектора 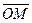 на оси координат. Числа X, Y, Z называются координатами вектора
на оси координат. Числа X, Y, Z называются координатами вектора 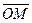 . Соотношение (*) устанавливает взаимно однозначное соответствие между векторами и упорядоченными тройками чисел – координатами векторов.
. Соотношение (*) устанавливает взаимно однозначное соответствие между векторами и упорядоченными тройками чисел – координатами векторов.
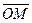 = {X, Y, Z}.
= {X, Y, Z}.
i = {1, 0, 0}; j = {0, 1, 0}; k = {0, 0, 1}.
Действия над векторами, заданными своими координатами.
1. При сложении векторов их одноименные координаты складываются, а при вычитании вычитаются.
a ± b = X 1 i + Y 1 j + Z 1 k ± (X2 i + Y2 j + Z 2 k) = (X 1 ± X2) i + (Y1 ± Y2) j ± ( Z1 ± Z 2) k.
2. При умножении вектора на число координаты его умножаются на то же число.
a = X 1 i + Y 1 j + Z 1 k. λ a = λ X 1 i + λ Y 1 j + λ Z 1 k.
Следствие.
Условие коллинеарности (параллельности) векторов. Пусть a ║ b. b = |b|/|a| ∙a.
|b|/|a| = λ, b = λ a. Тогда получим X2 = λ X1, Y2 = λY1, Z2 = λZ1.

Скалярное произведение векторов.
Рассмотрим два вектора a и b.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
 (a b) = |a| |b| cos φ = a| |b| cos
(a b) = |a| |b| cos φ = a| |b| cos 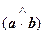
b
 φ a
φ a
Заметим, что | b | cos φ = пр a b. Следовательно, (a b) = | a| пр a b или (a b) = | b| пр b a.
Понятие скалярного произведения имеет свой источник в физике. Действительно, если a - сила, b – перемещение, то (a b) – работа этой силы.