Свойства скалярного произведения.

1.

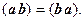
2. ( λ a) b = λ(ab),

Доказательство.

.

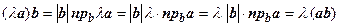3. a(b + c) = (ab) + (bc).

Доказательство.

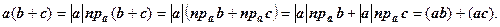
4. Если векторы a и b перпендикулярны, то ( ab) = 0.

5. Если скалярное произведение двух ненулевых векторов равно нулю, то векторы перпендикулярны.

 

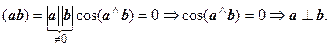
Скалярное произведение в координатах.

Пусть векторы a и b заданы своими координатами

a = {X₁, Y₁, Z₁}, b = {X₂, Y₂, Z₂}

Тогда

(a b) = (X₁ i + Y₁ j + Z₁ k) (X₂ i + Y₂ j + Z₂ k).

(i i) = i² = | i| |i| cos 0 = 1, аналогично (j j) = (k k) = 1, (i j) = (i k) =…= 0.

Отсюда

(ab) = X₁X₂ + Y₁Y₂ + Z₁Z₂.

 

Угол между векторами.

b

φ a (ab) = | a | | b |, cos =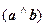

 

Если векторы a и b заданы своими координатами, то

 

cos = .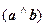

П р и м е р.

a = {1, 2, -3}, b = {-1, 3, 1}. cos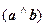

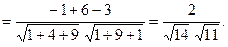
Проекция вектора на вектор.

(ab) = |b| пр _ba

a

b пр _ba =

 

Векторное произведение.

Векторным произведением двух векторов a и b называется третий вектор с, длина которого равна площади параллелограмма, построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный в ту сторону, что если смотреть с конца его, кратчайший поворот от a к b представляется происходящим против часовой стрелки (векторы a, b, с образуют правую тройку).

c = [ ab ] [ ab ] = c a

| c| = S _пар = | a| |b| sin(a^b).

b b

c = [ ab ]

a

Свойства векторного произведения.

1. [ ab } = −[ ba ],

a

 

b

 

c = [ ab ]

 

 

2. [λ ab ] = λ[ ab ] или [ a λ b ] = λ[ ab ]

3. [ a (b + c)] = [ ab ] + [ ac ],

4. Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.

Необходимость. Пусть a ║ b.

(a^ b) = 0

a b

 

ba (a^ b) = π

 

| c| = 0.

 

Достаточность.

Пусть | c | = 0. | a | | b | ≠ 0→ sin(a b) = 0, a ║ b.

Векторное произведение в координатах.

Пусть векторы a и b заданы своими координатами

a = {X₁, Y₁, Z₁}, b = {X₂, Y₂, Z₂}.

[ ab ] = [(X₁ i + Y₁ j + Z₁ k) (X₂ i + Y₂ j + Z₂ k)].

[ i i ] = [ j j ] = [ k k ] = 0, [ i j ] = k, [ j k ] = i, [ k i ] = j.

I j

 

k

 

 

[ ab ] = (Y₁Z₂ – Z₁ Y₂) i – (X₁Z₂ – Z₁X₂) j + (X₁Y₂ – Y₁X₂) k = .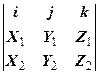

П р и м е р. Найти площадь треугольника, построенного на векторах a = {2, -1, 0}, b = {1, 1, -2}.

c = [ ab ], S_пар = | c |, S_Δ= ½ | c|.

b

 

a

 

Смешанное произведение.

Рассмотрим три вектора a, b, c. Пусть [ ab ] = d. Тогда (dc) = [ ab ] c = (abc) – смешанное или векторно-скалярное произведение.

Геометрический смысл смешанного произведения.

d Рассмотрим параллелепипед, построенный на векторах a, b, c.

a, b, c – правая тройка. Пусть d = [ ab ].

c h 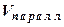= S_осн h, S_осн = | d|.

 

b

a

 

 

h = пр _d c, 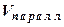= | d| 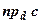= (dc) = (abc).

Пусть векторы a, b, c образуют левую тройку (вектор d направлен вниз).

c

h

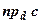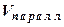a h = - , = - d =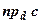

 

b = - (abc).

 

d

Смешанное произведение есть число, абсолютная величина которого равна объему параллелепипеда, построенного на перемножаемых векторах как на ребрах.

Смешанное произведение в координатах.

Пусть векторы a, b, c заданы своими координатами

a = {X₁, Y₁, Z₁}, b = {X₂, Y₂, Z₂}, с = {X₃, Y₃, Z₃}.

Тогда

d = = .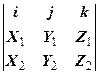

(abc) = [ ab ] c = .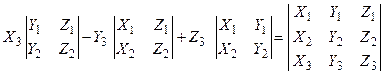

Справедливость равенства доказывается путем разложения определителя третьего порядка по элементам третьей строки.

П р и м е р. Вычислить объем треугольной пирамиды, построенной на векторах AB = {3, 2, 4}, AC = {3, 5, -1}, AD = {2, 3, 5}.

D

A C

 

B

V пирам = ¹/₃ V призмы = ¹/ ₆ V параллелепипеда. V параллелепипеда = |(abc) |

(abc) = = 14,

 

V пирамиды = ¹⁴/₆ = ⁷/₃.

Условие компланарности трех векторов.

Векторы a, b, c называются компланарными, если они параллельны одной и той же плоскости.

a

b Условие компланарности векторов

c

 

(abc) = 0