Для того чтобы найти собственные формы крутильных колебаний стержня, нужно рассмотреть задачу собственных колебаний стержня.
Тогда уравнение примет вид:
(14)
Разделим на 
и разнесем в разные части частные производные:
(15)
Собственные формы будем находить по методу Фурье (методу разделения переменных):
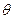(x,t) = X(x) ∙ T(t) (16)
Так как процесс свободных колебаний – процесс гармонический, то:
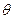(x,t) = X(x) ∙ sin(ωt), (17)
где ω – частота свободных колебаний балки.
С учётом формулы (21):
; 
;
; 
.
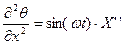Подставим найденные частные производные в уравнение (14):
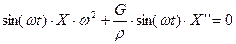(18)
Вынесем за скобку общий множитель sin(ωt):
(19)
Разделим выражение (19) на sin(ωt) 
. И получим:
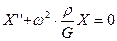(20)
Общим решением уравнения (20) является функция:
(21)
Теперь используя граничные условия для свободных колебаний, найдем собственные частоты.
Граничные условия:
а) 
б)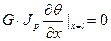 
Из а) функция (18) принимает вид:
=> 
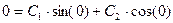Из б):
=> 
=> 
Из а) и б) получаем:
=> 
=0
, (22) где n = 0,1,2,..
В итоге получаем спектр собственных частот:
, (23)
где n = 0,1,2,..
2.3. Определение частного вида функции угла закручивания θ(x,t)
Возвращаемся к задаче на неустановившиеся колебания.
Используем метод собственных функций (метод разложения по собственным формам). При этом должны быть заданы граничные условия, а так же начальные условия:
Начальные условия:
а) 
;
б) 
Тогда решение строится в виде:
(25)
Метод Бубнова-Галеркина приводит к уравнениям:
, (26)
где i = 1,2,3,..
В силу ортогональности базисных функций ненулевыми коэффициентами будут те, в которых (i = n), тогда:
(27)
Разделим выражение (30) на 
:
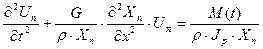(28)
Примем собственную форму равную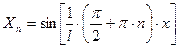 
, тогда:
;
.
Так как момент находится на конце стержня, то
(29)
Подставим найденные производные и (29) в выражение (28):
(30)
Упрощаем:
(31)
Получили выражение вида:
, (32)
где 
, 
.
Решение уравнения (36) может быть представлено в виде интеграла Дюамеля:
(33)
Константы 
и 
найдем из начальных условий:
а) 
;
б)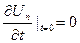 
.
Из а)
=> =0
Так как момент на конце импульсный, то рассмотрим его на рисунке (рис. 3):
Рис. 3. Графическое изображение изменение импульса во времени
Из рисунка видно, что момент изменяется в соответствии с системой уравнений:
Тогда интеграл Дюамеля будет равен:
(34)
Найдем 
(35)
(36)
Далее используем второе начальное условие (б), получаем:
=> =0
Таким образом, выражение (34) преобразуется в:
(37)
Подставляем выражение (37) в общее решение для угла закручивания.
В конечном итоге, выражение для угла закручивания принимает вид:
(38)
Константы С1 и С2 определяются конкретными граничными условиями.
Вышеописанные формулы и функции были выведены для однородного сплошного стержня.
Заключение
В курсовой работе была решена задача о колебаниях слоистого стержня, вызванных действием импульсного крутящего момента. В процессе работы над курсовой работой, ознакомился с программой MathCad. С помощью встроенных функций MathCadа рассчитал константы и построил графики.
Список литературы
1. Болотин В.В., Колебания линейных систем. – М.: Изд-во «Машиностроение»,1978. – 352 с
2. Тимошенко С.П., Янг Д.Х., Уивер У. Колебания в инженерном деле. – М.: Изд-во «Машиностроение»,1985. – 472 с
3. Чекалкин А.А., Котов А.Г. Динамика и устойчивость композитных конструкций: учебное пособие. - Пермь: Изд-во ПГТУ, 2006. - 65 с
4. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. - М.: УРСС, 2002. - 319 с