Проект «Открытая школа»
2 марта 2019 года
https://vk.com/mif.openschool
Лекция «Метод вспомогательной окружности при решении планиметрических задач»
Ковалева Галина Ивановна
Материалы лекции
Метод вспомогательной окружности
Условия, при которых четыре точки лежат на одной окружности:
1. Можно указать точку, равноудаленную от рассматриваемых точек А, В, С и D.
2. Из точек С и D, лежащих по одну сторону от прямой АВ, отрезок АВ виден под одним и тем же углом.
3. Из точек С и D, лежащих по разные стороны от прямой АВ, отрезок АВ виден под углами, сумма которых равна 180°.
4. Из точек С и D отрезок АВ виден под прямым углом.
Задачи, рассмотренные на лекции
1. В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.
2. В трапеции ABCD углы DAC и DBC равны. Докажите, что трапеция равнобедренная.
3. В остроугольном треугольнике ABC проведены высоты BB1 и CC1. Докажите, что углы BB1C1 и BCC1 равны.
4. В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
5. Известно, что ВМ и CN – высоты остроугольного треугольника ABC, при этом MN = 14 и BC = 50. Найдите расстояние между серединами MN и BC.
6. Диагонали трапеции перпендикулярны боковым сторонам. Докажите, что трапеция равнобедренная. Найдите площадь трапеции, если её основания равны 10 и 26.
7. Вне прямоугольного треугольника АВС на его гипотенузе АВ построен квадрат АВКМ. Докажите, что угол АСО равен углу ОСВ, где О – точка пересечения диагоналей квадрата.
8. В остроугольном треугольнике АВС проведены высоты АР и СQ.
а) Докажите, что угол BPQ равен углу BAC.
б) Найдите PQ,если известно, что площадь треугольника АВС равна 96, площадь четырехугольника AQPC равна 72, а радиус окружности, описанной около треугольника ABC равен 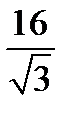 .
.
9. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что AC – биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC =15 и BD =8,5.
10. В треугольнике АВС проведены медианы АА1, ВВ1, СС1. Найдите длину медианы СС1, если АВ =  , а угол С равен углу между АА1 и ВВ1.
, а угол С равен углу между АА1 и ВВ1.
Задачи для самостоятельного решения
(аналогичные рассмотренным на лекции)
1. В выпуклом четырёхугольнике ABCD углы BCA и BDA равны. Докажите, что углы ABD и ACD также равны.
2. В трапеции ABCD углы CDB и CAB равны. Докажите, что трапеция равнобедренная.
3. В трапеции ABCD с основаниями AD и BC углы ABD и ACD равны. Докажите, что трапеция равнобедренная. Найдите площадь трапеции, если AD = 7 и BC = 5, а угол ∠ ACD = 60°.
4. В остроугольном треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы AA1B1 и ABB1 равны.
5. В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
6. Из произвольной точки М катета АС прямоугольного треугольника АВС опущен перпендикуляр МК на гипотенузу АВ. Докажите, что угол МКС равен углу МВС.
7. Известно, что ВМ и CN – высоты остроугольного треугольника ABC, при этом MN = 10 и BC = 26. Найдите расстояние между серединами MN и BC.
8. В остроугольном треугольнике АВС проведены высоты АР и СQ.
а) Докажите, что угол PAC равен углу PQC.
б) Найдите радиус окружности, описанной около треугольника ABC, если известно, что PQ = 8 и ∠ ABC = 60°.
9. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что AC – биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC =12 и BD =6,5.
10. В треугольнике АВС проведены медианы АА1, ВВ1, СС1. Найдите длину медианы ВВ1, если АC =  , а угол В равен углу между АА1 и СС1.
, а угол В равен углу между АА1 и СС1.
Дополнительные задачи
(задачи для самостоятельного решения)
1. В трапеции ABCD боковая сторона АВ перпендикулярна основания. Из точки А на сторону CD опустили перпендикуляр АН. Точка Е принадлежит стороне АВ, прямые CD и СЕ перпендикулярны.
а) Докажите, что ВН параллельна прямой ЕD.
б) Найдите отношение ВН к ЕD, если ∠ BCD = 135°.
2. В остроугольном треугольнике АВС проведены Высоты АК и СМ. В треугольнике МКС из вершины К проведена высота КН к стороне МС. Аналогично в треугольнике КМА из вершины М проведена высота МЕ к стороне АК.
а) Докажите, что прямая ЕН параллельна прямой АС.
б) Найдите отношение ЕН к АС, если ∠ ABC = 60°.
3. Точка О – центр окружности, описанной около остроугольного треугольника АВС. На продолжении АО за точку О отмечена точка К. Известно, что ∠ ВAC +∠ AКC = 90.
а) Докажите, что четырехугольник ОВКС описанный.
б) Найдите радиус окружности, описанной около четырехугольника ОВКС, если известно, также, что cos∠ ВAC = 0,6 и BC = 48.
4. Высоты ВВ1 и СС1 остроугольного треугольника АВС пересекаются в точке Н.
а) Докажите, что ∠ AНВ1 = ∠ ACВ.
б) Найдите ВС, если АН = 21 и ∠ BАC = 30°.
5. На диагонали параллелограмма взяли точку, отличную от её середины. Из неё на все стороны параллелограмма (или их продолжения) опустили перпендикуляры.
а) Докажите, что прямая ЕН параллельна прямой АС.
б) Найдите отношение ЕН к АС, если ∠ ABC = 60°.