Этап 1. Расчёт колебаний привода машины.
Составление динамической модели машины.
Составим динамическую модель привода для системы с тремя степенями свободы Н=3.
Mдв. Вал 1
 | |||||
 |  | ||||
φ 
1 φ1
С1
Вал 2
 | |||||
 | |||||
 | |||||
φ2 λ1 φ3
 |
Вал 3
φ4
 |
С2
Хпр
 | |||||||||
 |  | ||||||||
 | |||||||||
 | |||||||||
х5 λ2
Выбор обобщённых координат.
При выполнении данной процедуры следует отдавать предпочтение обобщенным координатам, соответствующим сравнительно малым относительным перемещениям, которые и отображают колебания в системе.
В качестве первой обобщённой координаты примем абсолютную координату в начале кинематической цепи – угол поворота двигателя:
= 
= 
= * 
= * 
, = = 
= 
+ 
= * +
= * 
=( * + )* 
, = = 
= * 
=( * + )* * 
, = 
= + 
=( * + )* * +
= * * + *
= * * * + * *
= * * * + * * 
+
1.3 Кинематические хар-ки: 
= 
= 
= 0,86364
= 
= 
= 0,90476
1.4 Инерционные хар-ки:
При расчёте моментов инерции зубчатых колёс примем их в виде сплошных дисков с наружными диаметрами, соответствующим диаметрам делительных окружностей зубчатых колёс. В этом случае момент инерции колеса относительно оси вращения, проходящей через его центр масс, определяется из соотношения:
= 
, где 
– масса i колеса
– радиус делительной окружности i колеса
Данный радиус определяется из выражения:
= 
, где 
- модуль i зацепления, в данной работе он равен: = 0.004 м
– число зубьев колеса
= 
= 0.076 м 
= 
= 0.00694 
= 
= 0.088 м 
= 
= 0.01239
= = 0.076 м 
= 
= 0.00404
= 
= 0.084 м 
= 
= 0.01023
1.5 Упругие хар-ки:
Крутильная жесткость участка вала постоянного диаметра определяется выражением:
= 
, где 
- коэффициент крутильной жесткости участка вала
G – модуль сдвига (для конструктивных сталей G= 
- длина участка i вала
= 
- полярный момент инерции поперечного сечения на участке вала,
где 
- диаметр i вала
В задании 6/4 
= 
= 650000 Нм
При расчёте 
следует учесть, что он находится на вале 2 и в формулу полярного
момента подставляется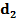 
= 32 мм = 0.032 м, а в формулу коэффициента крутильной жесткости 
= 480 мм = 0.48 м
= 
= 
= 
= 17157,2843 
Определение инерционных коэффициентов
Для динамической модели, имеющей Н=3, величина кинетической энергии в квадратичной форме может быть представлена выражением:
T = 
( 
+ 
+ 
+2 
+ 2 
+2 
)
Определение значений 
основан на приравнивании соответствующих членов в выражениях для кинетической энергии, записанной в общем виде и для конкретной схемы. В нашем случае она имеет вид:
T = ( 
+ 
+ 
+ 
+ 
+ 
+ 
) =
= [ 
+ 
+ 
+ 
+ 
+
+ 
+ 
]
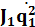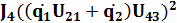Приравнивая соответствующие коэффициенты при 
, 
, 
, 2 
, 2 
, 2 
в выражениях выше, получим:
= 
+ 
+ 
+ 
+ 
+ 
+ 
= 
+ 
+ 
+ 
= 1,033615
= 
= 175
= ( + + + 
) 
= 0.76528
= 
= 0.9654
= 
= 
= 13,3000
1.7 Находим квазиупругие коэффициенты:
Для динамической модели с Н=3 потенциальная энергия в квадратичной форме может быть представлена выражением:
V = ( 
Практический приём определения 
аналогичен определению , в нашем случае потенциальная энергия в функции обобщённых координат имеет вид:
V = [ 
+ 
( 
] = ( 
)
= 
= 17157,2843 Hм
= 
= 650000 Hм
= 0
= 
= 0
= 
= 0
= 
= 0
Составим частотное уравнение привода и определим собственные
частоты:
Составление системы дифференциальных уравнений производится на базе уравнения Лагранжа 2го рода, в нашем случае Н=3 и система имеет вид:
 |
= 
= 
= 
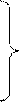Координата 
является циклической, поскольку она в явном виде не входит в выражение для кинетической и потенциальной энергии.
Для определения собственных частот используются 2 последних уравнения системы дифференциальных уравнений с правой частью, приравненной к 0:
+ 
= 0
+ 
= 0
Решение этой системы уравнений имеет вид:
 |
= 
= 
,
где 
- амплитуда колебаний
- собственная частота колебаний, 
- фаза колебаний
– начальная фаза (i =1, 2)
Составим частотное уравнение для этой системы:
Δ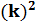 
= 
, где k – собственная частота, 
В раскрытом виде с учетом 
биквадратное уравнение имеет вид:
или в свёрнутой форме: 
После раскрытия определителя получаем биквадратное уравнение, решение которого даёт 2 действительных корня – 2 собственные частоты:
Определим низшую собственную частоту по методу Данкерлея:
1.9 Определение коэффициентов формы:
По основной формуле: По проверочной формуле:
1.10 Определение парциальных частот:
Парциальные частоты определяются при последовательном закреплении всех обобщённых координат кроме одной, поэтому при 
вычисляем значение 
, а при 
- значение 
:
