Для выполнения этапа выбираем вал 2 исходного механизма с двумя расположенными на нём массами – зубчатыми колёсами 2 и 3. Расчётную схемы балки выбираем из таблицы, у нас она под номером 1. Ограничиваясь рассмотрением изгибных колебаний в одной из плоскостей, перейдем сначала к безынерционному упругому «скелету» балки. Для этого к связи, кроме внешних сил 
и 
, приложим в соответствии с принципом Даламбера силы инерции 
и 
, где 
и 
- прогибы под соответствующими массами 
и 
. Таким образом, задача сведена к типовой схеме балки, подверженной воздействию сил инерции 
и 
, определяемых из зависимостей:
При этом по аналогии:
, где 
– коэффициенты податливости (влияния)
Рассчитываем по формулам:
, 
,
, 
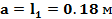d – диаметр вала = 0.032 м
- осевой момент инерции поперечного сечения вала
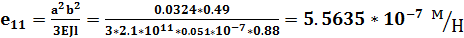
Система однородных дифференциальных уравнений, описывающая свободные колебания балки, при нулевых значениях обобщённых сил:
Решением этой системы уравнений будет:
, где A и В – амплитуды изгибных колебаний вала, м
После подстановки выражений в систему получаем, что при условии А≠0, В≠0 (нетривиальное решение) собственные частоты 
должны быть корнями частного уравнения:
После раскрытия определителя имеем:
Или в свёрнутой форме:
, где:
, 
,
Решение этого уравнения даёт 2 действительных корня – 2 собственные частоты изгибных колебаний вала, причем 
:
Низшая частота по методу Данкерлея:
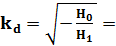0.0596* 
Коэффициенты формы:
По основной формуле: По проверочной формуле:
Этап 4. Решение задачи виброизоляции. Построение диаграммы 
. Построение АЧХ и ФЧХ для одномассовой модели.
При работе машины из-за воздействия внешних сил и неуравновешенности инерционных нагрузок возникают периодические вынуждающие силы, передающиеся на несущие конструкции и фундамент машины.
Если машину жестко закрепить на фундаменте, то на него полностью будут передаваться нагрузки, возникающие в машине. Однако в случае постановки машины на упругую подвеску и при соответствующем подборе параметров подвески переменная составляющая реакции на фундамент может быть существенно сниженаю При этом осуществляется так называемая выброизоляция машины.
В общем виде условие выброизоляции состоит в реализации неравенства вида:
- номинальное и допустимое значение коэффициента динамичности
- номинальное и допустимое значение амплитуды вынужденных колебаний
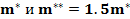- предельные значения массы машины на упругом основании
1) Из условия обеспечения максимально допустимого коэффициента динамичности:
2) Из условия обеспечения минимально допустимой амплитуды вынужденных колебаний:
При m = 0:
При m = 
и 
:
3) Из условия ограничения велечины осадки машины Δ под действием её собственного веса:
При m = 0, 
При m = :
4) Выполняем проверку результатов:
4.1 Находим собственную частоту:
4.2 Проверяем коэффициент динамичности:
,
допустимое значение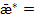 
4.3 Проверяем амплитуду вынужденных колебаний:
,
допустимое значение 
4.4 Проверяем осадку машины под действием колебаний:
,
допустимое значение: 
Таким образом, все поставленные на данном этапе условия.