ПРЯМАЯ НА ПЛОСКОСТИ
Вспомним основные уравнения прямой на плоскости.
Общее уравнение прямой на плоскости имеет вид:
Ax+By+C=0. Уравнение прямой с угловым коэффициентом k:
y=kx+b. Уравнение прямой с угловым коэффициентом, проходящей через точку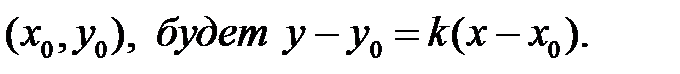 
Уравнение прямой, проходящей через две точки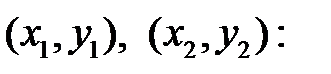 
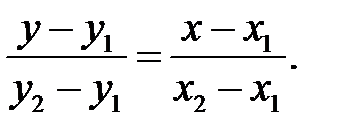Уравнение плоскости в отрезках 
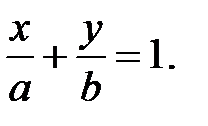Отрезки
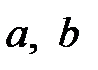отсекаются на осях координат.
Угол между двумя прямыми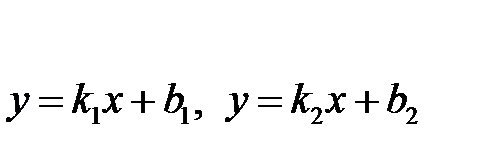 
вычисляют с помощью формулы
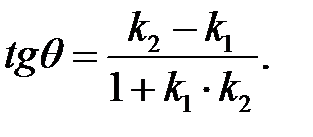
Для этих прямых условие параллельности определяется как
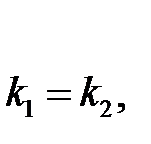а перпендикулярности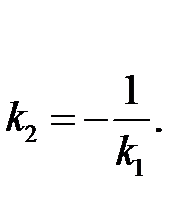 
Расстояние от точки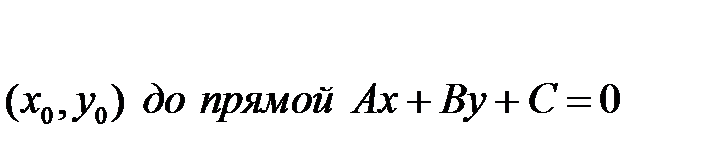 
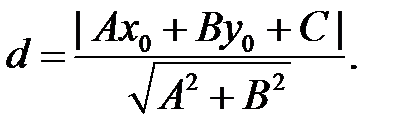
Рассмотрим несколько примеров.
1. Найти уравнения прямой, которая проходит через точку А(3,-1) параллельно и перпендикулярно прямой
4x-2y+5=0.
В обоих случаях используем уравнение прямой с угловым коэффициентом, проходящей через точку. Первоначальную прямую запишем как y=2x+5/2. У ней угловой коэффициент к=2. В случае параллельной прямой возьмем этот же к. Тогда y+1=2(x-3) или y=2x-7. Для перпендикулярной прямой угловой коэффициент равен -1/2. Эта прямая определится из уравнения y+1=-(1/2)(x-3). Оно приводится к виду x+2y-1=0.
2. Какие отрезки отсекает прямая 2x-3y+12 на осях координат?
Здесь нужно использовать уравнение плоскости в отрезках.
Сделаем следующие преобразования: 2x-3y=-12,
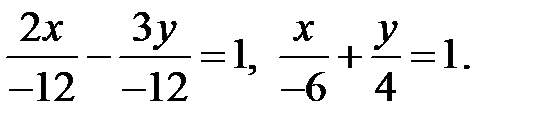
Следовательно, на оси OX отсекается отрезок, равный -6, а на оси OY - 4. В этом случае легко построить график исходной прямой.
3. Найти уравнение прямой, проходящей через 2 точки А(5, -3) и В(2, 1).
Здесь имеем: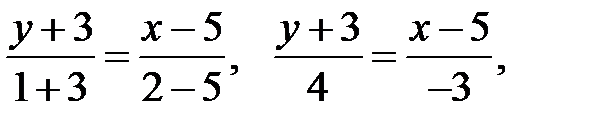 
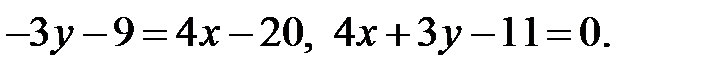
Можно проверить, что точки А и В лежат на этой прямой.
4. Найти угол между двумя прямыми 3x-2y+6=0, 2x+y-4=0.
Определим угловые коэффициенты этих прямых. Представим уравнения прямых в виде y=(3/2)x+3, y=-2x+4. Отсюда видим, что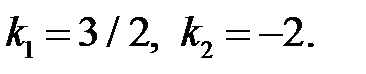 
Угол можно найти из равенства
|
|
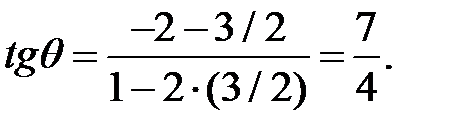
5. Найти расстояние от точки А(3, 1) до прямой 4x-y-6=0.
Используя приведенную выше формулу, сразу получим
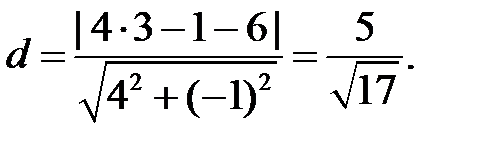
КРИВЫЕ ВТОРОГО ПОРЯДКА
Мы рассмотрим окружность, эллипс, гиперболу, параболу.
1. Составить уравнение окружности, имеющей центр в точке
С(5, -2) и радиус R=3.
Каноническое уравнение окружности имеет вид:
. 
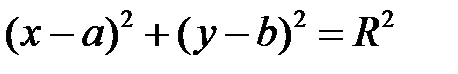Здесь a, b – координаты центра окружности. В нашем случае искомое уравнение определится как
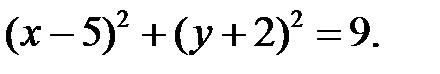
2. Привести к каноническому виду уравнение
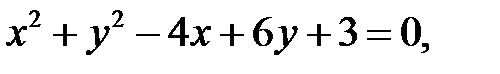
определить вид кривой и ее параметры.
Выделим полные квадраты по x, y:
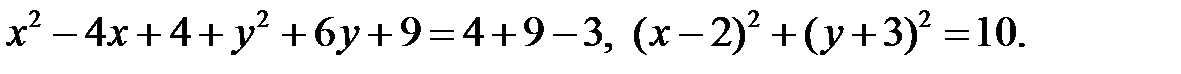
Это есть уравнение окружности с центром в точке (2, -3) и радиусом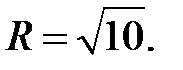 
3. На оси абсцисс найти центр окружности, проходящей через точки А(5, -1), В(2,4), и написать уравнение этой окружности.
Здесь b=0 и точка центра будет С(а,0). Тогда уравнение можно записать как
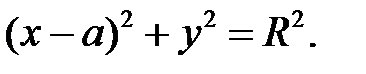
Подставим сюда координаты точек А и В:
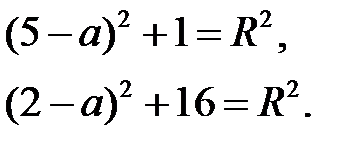
Приравняем левые части этих равенств:
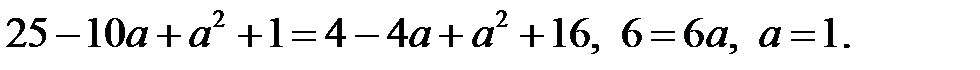
Затем найдем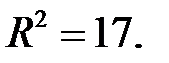 
Точка центра будет С(1, 0).
Уравнение окружности запишем как
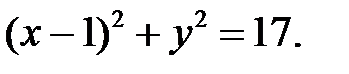
4. Составить уравнение эллипса, зная что расстояние между фокусами равно 8 и большая полуось равна 6.
Каноническое уравнение эллипса записывается в виде:
Здесь a и b – большая и малая полуоси эллипса. Расстояние между фокусами равно 2с=8, с=4,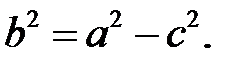 
В нашем случае а=6,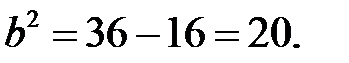 
Уравнение эллипса можно записать как
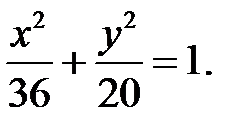
5. Составить уравнение эллипса, если большая полуось равна 6 и эксцентриситет ε=0,5.
В этой задаче а=6,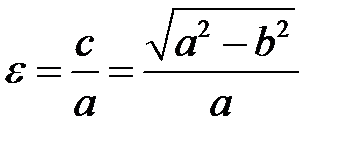 
. Тогда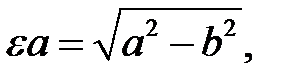 
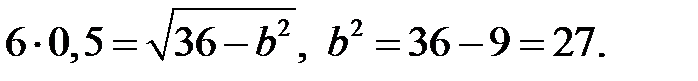Ответом будет уравнение
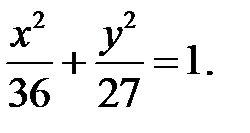
6. Найти длину полуосей, координаты фокусов и эксцентриситет эллипса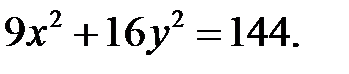 
Поделив уравнение на правую часть, получим
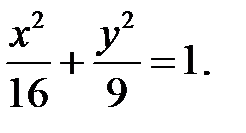
Отсюда видим, что полуоси равны a=4, b=3. Тогда
|
|
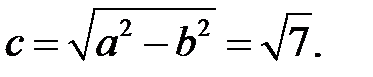Координаты фокусов запишем в виде:
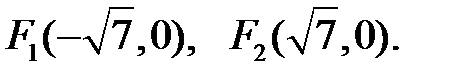Эксцентриситет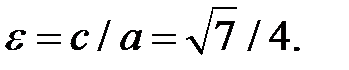 
7. Привести к каноническому виду уравнение
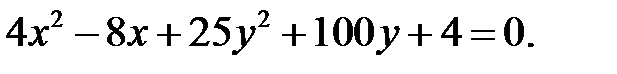
Выделим полные квадраты по x и y:
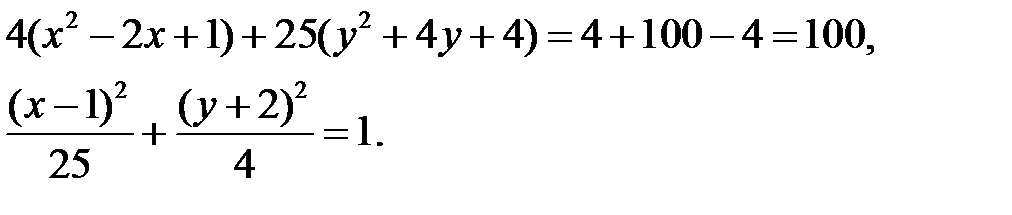
В итоге мы получили эллипс с центром в точке С(1, -2) и с полуосями a=5, b=2.
8. Составить уравнение гиперболы, зная, что ее вещественная ось равна 6 и гипербола проходит через точку (9, -4).
Каноническое уравнение гиперболы
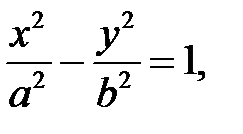
где а – вещественная полуось гиперболы, b – мнимая полуось. Нам нужно найти a и b. В данном случае 2а=6, а=3. Уравнение примет вид
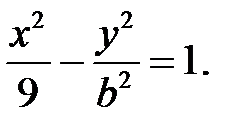
Подставим сюда координаты заданной точки:
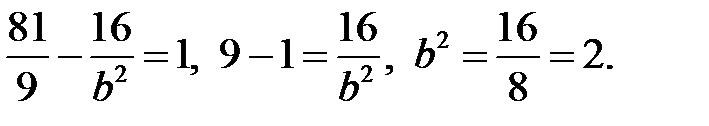
В итоге уравнение гиперболы примет вид: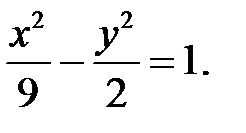 
9. Составить уравнение гиперболы, зная, что она проходит через точки М(2, -1) и N(3, 2). В уравнение
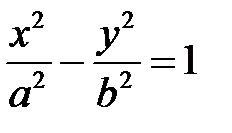
подставим координаты обеих точек. Получим систему двух уравнений
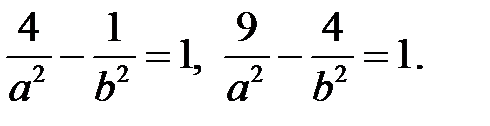
Из первого уравнения найдем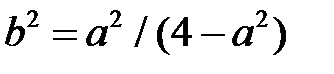 
и подставим
во второе уравнение. Получим
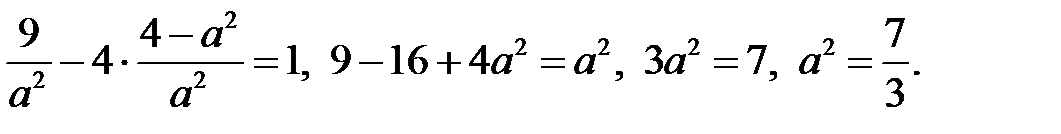
Нетрудно найти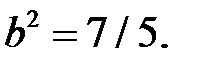 
Искомое уравнение гиперболы запишем как
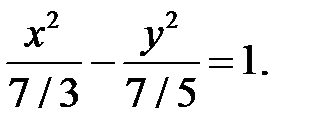
10.Определить вид кривой
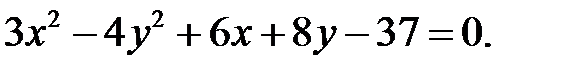
Сделаем следующие преобразования:
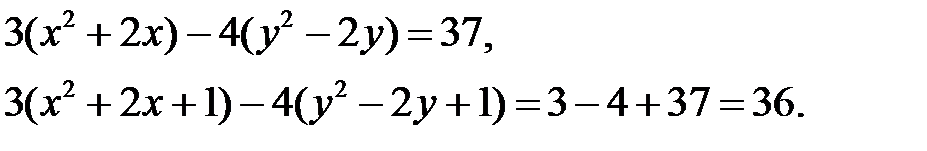
Поделим это выражение на 36 и в итоге получим:
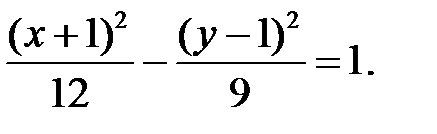
Это есть уравнение гиперболы с центром в точке (-1, 1) и с полуосями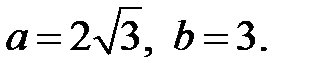 
11.Составить уравнение параболы, зная, что она симметрична относительно оси ОХ и расстояние фокуса от вершины равно 4.
Для этого случая каноническое уравнение параболы запишется как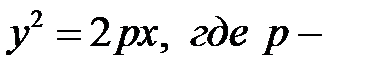 
параметр. Расстояние фокуса от вершины есть половина параметра, поэтому p/2=4, p=8 и в итоге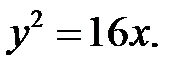 
12. Составить уравнение параболы, зная, что парабола симметрична оси ОУ, проходит через начало координат и через точку А(6, -2).
В данном случае берем другое каноническое уравнение параболы: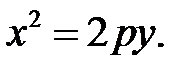 
Для определения р подставим сюда координаты точки А: 36=-4p. Определяем р=-9 и возвращаем в уравнение. Ответ: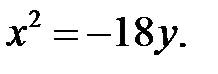 
|
|
13. Привести к каноническому виду следующее уравнение:
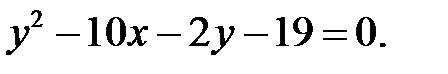
В этом случае
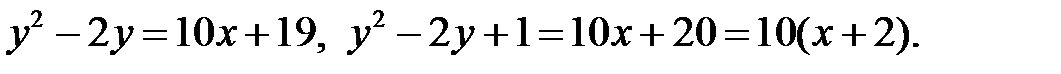
Уравнение параболы определится как
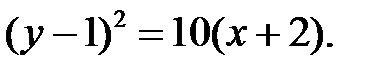
Вершина ее находится в точке (-2, 1), она симметрична оси, параллельной оси ОХ.