Будем проводить расчет тепловой трубы для солнечного коллектора, установленного под углом широты местности, равной 48°. Мощность коллектора должна составлять 700 Вт при температуре пара (Тгор = 60°С) на расстояние 0.4 м в условиях наличия гравитации.
Вначале проведем предварительный расчет солнечного коллектора, который начинается с определения энергоприхода на его поверхность, а также среднемесячное среднее дневное значение плотности солнечного излучения.
Следовательно, для обеспечения дома горячей водой,
Основой расчета тепловой трубы является определение потока передаваемой мощности при заданной температуре пара. Из условий удобства эксплуатации принимаем, что длина тепловой трубы равна 0,4 м (0,3 м – длина испарителя, 0,1 м – длина конденсатора), наклон трубы – 48°. Давление внутри трубы 0,01 МПа. Рабочая температура пара от 298 до 353 К.
В качестве материала корпуса выбрана медь, фитиль образован из двух слоев медной сетки в 200 меш на внутренней стенке трубы. Выбор схемы фитиля обусловлен простотой его изготовления. В качестве рабочей жидкости выбрана вода.
Конструкция вакуумной колбы с тепловой трубой внутри показана на рис. 7.2.

Рис. 7.2. Сечение вакуумной колбы: 1 – стеклянная колба; 2 – тепловая труба; 3 – пластина поглотителя
Для того чтобы тепловая труба работала, необходимо, чтобы удовлетворялось соотношение:
 (7.2)
(7.2)
где  – максимальный капиллярный напор;
– максимальный капиллярный напор;  – гравитационная составляющая полного падения давления;
– гравитационная составляющая полного падения давления; 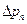 – перепад давления в потоке пара;
– перепад давления в потоке пара; 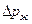 – перепад давления в потоке жидкости.
– перепад давления в потоке жидкости.
Для определения минимального проходного сечения по жидкости, обеспечивающего передачу заданной мощности, перепадом давления в паровом потоке можно пренебречь.
 (7.3)
(7.3)
 (7.4)
(7.4)
где  – поверхностное натяжение;
– поверхностное натяжение;  – радиус поры фитиля;
– радиус поры фитиля;  – краевой угол смачивания.
– краевой угол смачивания.
 (7.5)
(7.5)
где  – плотность жидкости; g – ускорение свободного падения; l – длина трубы; φ – угол наклона трубы.
– плотность жидкости; g – ускорение свободного падения; l – длина трубы; φ – угол наклона трубы.
 (7.6)
(7.6)
где 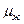 – вязкость жидкости (свойства жидкости берутся при Тгор = 60°С);
– вязкость жидкости (свойства жидкости берутся при Тгор = 60°С);  – максимальный тепловой поток; К – проницаемость фитиля; А – площадь поперечного сечения трубы; L – скрытая теплоты парообразования.
– максимальный тепловой поток; К – проницаемость фитиля; А – площадь поперечного сечения трубы; L – скрытая теплоты парообразования.
 (7.7)
(7.7)
Согласно расчету освещенности, величина солнечного излучения Рпср составляет Вт/м2. С учетом оптического КПД коллектора η = 0,9, на поглощательную поверхность (площадь Fпп м2) вакуумированной колбы в среднем приходится:
 (7.8)
(7.8)
 Вт.
Вт.
Определим расход жидкости в фитиле mmax из формулы (7.7), принимая Qср = Qmax:
 кг/с. (7.9)
кг/с. (7.9)
Определим максимальную теплопередающую способность трубы при максимальной температуре пара.
Выражение для максимального потока массы mmax можно получить, если принять следующие допущения:
· свойства жидкости не меняются вдоль трубы;
· фитиль является однородным;
· перепадом давления в паровом потоке можно пренебречь.
Тогда:
 (7.10)
(7.10)
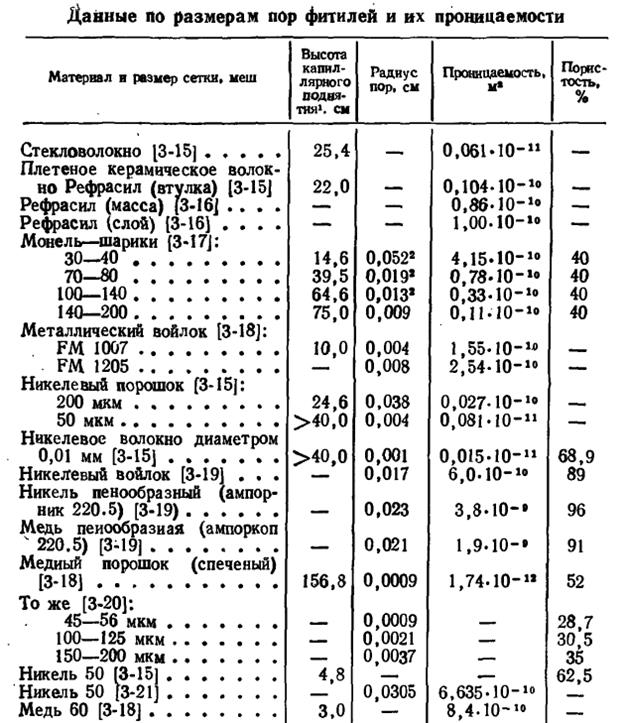
где rи – радиус поры в испарителе; выбирается сетка N меш (размер пор, например, 0.036 мм), тогда проницаемость сетки рассчитывается по формуле Блейка-Козени
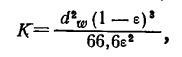
К = 8,4ꞏ10-10 м2, либо выбирается по значениям из табл.3
Диаметр проволоки равен 36 мкм, толщина двух слоев сетки составит 4*36=144 мкм. Внутренний диаметр корпуса трубы 6 мм. Тогда поперечное сечение фитиля А будет равно:
 м2. (7.11)
м2. (7.11)
Допустим наличие идеального смачивания (Θ = 0°), с учетом физических свойств воды, приведенных в табл. 7.1, определим максимальные расход жидкости и тепловой поток в фитиле.
Таблица 7.1
Физические свойства воды при Т = 353 К
| L, МДж/кг | ρж, кг/м3 | μж, мН/м | σ, Н/м |
| 2,3 | 0,36 | 0,0628 |
Пользуясь формулой (7.9) определяем, что  кг/с.
кг/с.
Подставив значение mmax в уравнение (7.6), получаем величину максимального теплового потока в фитиле: Qmax = Вт.
Термическое сопротивление стенки тепловой трубы в испарителе:
 (7.12)
(7.12)
где λм = 390 Вт/м2К – теплопроводность меди; lи – длина испарителя; t = 10-3 м – толщина стенки трубы; rвн = 0,004 мм – внутренний радиус испарителя.
Термическое сопротивление насыщенного жидкостью пара в испарителе:
 (7.13)
(7.13)
где rвнутр = 0,003 м – радиус парового канала; tф = 144 мкм – толщина фитиля.
Эффективная теплопроводность насыщенного фитиля:
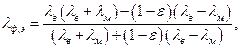 (7.14)
(7.14)
где λв = 0,668 Вт/м2К – теплопроводность воды; ε = 0,549 – проницаемость фитиля.
Термическое сопротивление парового потока:
 (7.15)
(7.15)
где Тп – температура пара; Fп – сопротивление пара; lк – длина конденсатора; ρп – плотность пара.
Термическое сопротивление насыщенного жидкостью фитиля в конденсаторе:
 (7.16)
(7.16)
где rк = 0,007 м – радиус конденсатора.
Термическое сопротивление стенки тепловой трубы в конденсаторе:
 (7.17)
(7.17)
Коэффициент теплопередачи тепловой трубы:
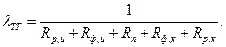 (7.18)
(7.18)
Перепад температуры между испарителем и конденсатором отнесенный к поперечному сечению трубы:
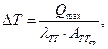 (7.19)
(7.19)
где 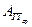 – среднее поперечное сечение по длине трубы.
– среднее поперечное сечение по длине трубы.
Полученные расчётные величины представлены в табл. 7.2.
Таблица 2
Сводная таблица расчетных величин
| Параметры | Величины |
| Rр,и, К/Вт | |
| Rф,и, К/Вт | |
| Rп, К/Вт | |
| Rф,к, К/Вт | |
| Rр,к, К/Вт | |
| λф,э, Вт/м2К | |
| λТТ, Вт/м2К | |
| Δ Т, К |
По результатам расчета минимальный перепад температур Δ Т между испарителем и конденсатором для начала работы тепловой трубы должен равняться Δ Т К Тепловой поток, передаваемый одной тепловой трубой при среднем значении освещенности, составил 35 Вт, следовательно, количество тепловых труб для обеспечения требуемой мощности коллектора равно:
 шт. (7.20)
шт. (7.20)