Провести термодинамический анализ процесса выращивания монокристаллов (или эпитаксиальных слоев) соединения CdTe n -типа проводимости из газообразных компонентов:

Считать, что основной процесс проводится в условиях замкнутого или квазизамкнутого объема. Парциальные давления пара исходных компонентов (pCd и pTe2) в системе необходимо задавать и поддерживать постоянными в течение всего процесса синтеза путем сублимации (или испарения) конденсированных фаз компонентов Cd и Te в независимых дополнительных температурных зонах реактора с температурами TA и TB соответственно.
- Расчет константы равновесия для основного процесса
Основной процесс получения бинарного полупроводникового соединения типа AIIBVI CdTe газофазным методом описывается уравнением:

Уравнение изотермы химической реакции:
ΔGT = ΔGoТ+ RTln(Πi piνi)
где ΔGoТ=-RTln(Kp) – изменение свободной энергии Гиббса при стандартных условиях.
Kp= (PСdPte20.5)0.5 -константа равновесия основного процесса.
ΔGT = -RTln(Kp) + RTln(Πi piνi)
ΔGT = RTln(PСdPte20.5)равн - RTln(PСdPte20.5)реальн
Расчитаем константу равновесия основного процесса основного процесса, для этого необходимо знать изменение свободной энергии Гиббса

ΔGo298 = ΔHo298 – 298ΔSo298
На основании закона Гесса расчитае стандартную энтальпию процесса ΔHo298:
ΔHo298=Σνi ΔHof,298(кон)- Σνi ΔHof,298(исх),
где νi-число молей вещества.
ΔHo298= ΔHof,298 (Cdteтв)-(ΔHof,298 (Cdг)+ ΔHof,298 (teг))=-70,82 кДж
Расчитаем стандартную энтропию процесса ΔSo298:
ΔSo298=Σνi ΔSof,298(кон)- Σνi ΔSof,298(исх)= ΔSof,298 (Cdteтв)-(ΔSof,298 (Cdг)+ ΔSof,298 (teг)) =-49,4 Дж/К
Изменение свободной энергии для стандартных условий процесса:
ΔGo298 = ΔHo298 – 298ΔSo298=-270148Дж.
Константу равновесия получаем равную:
lg(Kp) = - ΔGo298/(298Rln(10))=-47,45
Построим график зависимости lgPCdPTe21/2 от обратной температуры:

.
- Анализ процессов сублимации исходных компонентов
Анализ процесса сублимации Cd
Сублимация Cd рассматривается при температуре от 298 К до температуры плавления кадмия 594 К. Считаем, что пар Cd одноатомный.

Аналогично, используем уравнение изотермы химической реакции для стандартных условий, с учетом того, что для этого процесса РCd = Kp

Из справочных данных получаем


ΔGo298 = ΔHo298 – 298ΔSo298 = 111800 - 298∙115,84 = 77279,68 Дж
lg(Kp) = - ΔGo298/(298Rln(10))
Испарение Cd рассматривается при температуре от температуры плавления кадмия 594 К до температуры кипения кадмия 1040 К. Считаем, что пар Cd одноатомный.

Аналогично, используем уравнение изотермы химической реакции для стандартных условий, с учетом того, что для этого процесса РCd = Kp

Из справочных данных


Поскольку имеет место фазовый переход, то зависимость изменения энтальпии реакции от температуры приобретает более сложный вид.
Фазовый переход происходит для исходного компонента, поэтому энтальпия фазового перехода принимается отрицательной dHfpCd < 0

ΔGo594 = ΔHo298 – 594ΔSo298 + 298∫594ΔCpodT – 594298∫594(ΔCpo/T)dT = 111800 - 594∙115,84 -21,38∙(594-298) + 594∙21,38∙ln594/298 = 45.422 кДж
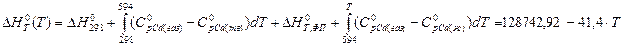

ΔGo900 = ΔHo298 – ΔHпл – 900(ΔSo298 + ΔSпл)+ 298∫594ΔCpodT – 900298∫594(ΔCpo/T)dT +
+ 594∫900ΔCpo’dT – 900594∫900(ΔCpo’/T)dT
| T,K (расчет) | lnKp (расчет) | T,K (эксперимент) | lnKp (эксперимент) |
| -13,55 | -13,88 | ||
| -3,996 | -3,88 | ||
| -0,98 | -0,88 |

|
Рис. 2.1. Зависимость десятичного логарифма константы равновесия
процесса испарения и сублимации кадмия от обратной температуры
Анализ процесса сублимации Te
 .
.
Найдем условие протекания процесса сублимации:
DGT= – RTln(Kp) + RTln(Пi pivi), где Кр =  – константа равновесия процесса сублимации теллура.
– константа равновесия процесса сублимации теллура.
DGT= RTln  реал – RTln
реал – RTln  равн.
равн.
Процесс может протекать лишь при условии, что DGT < 0, а это возможно лишь при условии:  равн >
равн >  реал.
реал.
Рассчитаем константу равновесия аналогично основному процессу, но с учетом фазового перехода.

При Т=298 К: 


При Т=723 К:
 , где
, где  .
.
 , где
, где  .
.
 .
.
При Т=1260 К: 
 , где
, где 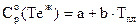 .
.
| Т, К | 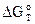 , кДж , кДж
| 
| 
|
| 58,97 | -10,34 | -20,68 | |
| 24,71 | -1,79 | -3,58 | |
| 11,52 | -0,48 | -0,96 |

|
Рис. 2.2. График зависимости десятичного логарифма равновесного давления пара теллура от обратной температуры для процесса сублимации.
- Построение линий трехфазного равновесия (P-T диаграмм)
С позиции термодинамики основной процесс должен самопроизвольно происходить при выполнении условия ΔG0T < 0, и следовательно

причем величина отношения парциальных давлений компонентов pCd / pTe2 безразлична.
С точки зрения кинетики процесса, скорость массопереноса компонентов через газовую фазу и скорость процесса в целом, будет наибольшей при некотором оптимальном отношении давлений pCd / pTe2. Найдем минимум зависимости общего давления газообразной фазы от давления одного из компонентов:

где 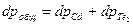 . Воспользуемся связью давлений через константу равновесия основного процесса
. Воспользуемся связью давлений через константу равновесия основного процесса 
 Þ
Þ 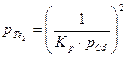
Тогда ищем производную общего давления по давлению кадмия:

Установим связь между парциальными давлениями кадмия и теллура через константу равновесия основного процесса


 Построим диаграммы линий трехфазного равновесия, на которых покажем линию, соответствующую давлению pCd над чистым Cd, линию минимального общего давления в системе и линию, соответствующую давлению pTe2 над чистой Te, пересчитанному в pCd через константу равновесия. Предполагаем, что линия термодинамического p-n-перехода (n = p) совпадает с линией минимального общего давления в системе.
Построим диаграммы линий трехфазного равновесия, на которых покажем линию, соответствующую давлению pCd над чистым Cd, линию минимального общего давления в системе и линию, соответствующую давлению pTe2 над чистой Te, пересчитанному в pCd через константу равновесия. Предполагаем, что линия термодинамического p-n-перехода (n = p) совпадает с линией минимального общего давления в системе.

|
Рис. 3.1. P-T диаграмма для сульфида кадмия (в координатах десятичного логарифма
давления паров кадмия от обратной температуры).

|
Рис. 3.2. P-T диаграмма для теллурида кадмия (в координатах десятичного логарифма
давления паров теллура от обратной температуры).
Область p-типа электропроводности соответствует давлению паров теллура, превышающему стехиометрическое, и давлению паров кадмия, меньшему стехиометрического.
- Расчет парциальных давлений паров компонентов, обеспечивающих протекание основного процесса в прямом направлении
Для нахождения парциальных давлений паров компонентов, обеспечивающих протекание основного процесса в прямом направлении воспользуемся связь давлений компонентов через константу равновесия и отношением давлений pCd / pTe2.
pCd / pTe2 = 0,01
Видно, что pCd / pTe2 принадлежит диапазону - 0,051 < pCd / pTe2 <2
Произведение давлений зависит от константы равновесия основного процесса
pCd (pTe2)1/2=1/Кр
Выбираем рабочую точку так, чтобы для основного процесса выполнялось при Т =ТAB

(PСdPte20.5)равн < (PСdPte20.5)реальн
Зададимся рабочей температурой основного процесса TAB = 1092 К. Тогда значение
lg(PСdPte20.5)равн = 3,5
Логарифм произведения давлений должен быть больше этой величины
lg(PСdPTe20.5)реал = 5,75
lg(PСdPTe20.5)реал > 3,5
Таким образом, отношение давлений задано pCd / pte2, а произведение lg(PСdte20.5)реал. Решаем систему
pCd / pTe2 = 0,05
PСd(PTe2)0.5 = е5,75
Отсюда получаем: PСd = 0,0498 атм
Pte2 = 0,017 атм
Точки пересечения уровня требуемого давления и линии давления паров вещества над чистым веществом дают температуру подогревных зон кадмия и теллура.
ТСd =847 К
Тte2 = 625 К
- Оценка возможности окисления кадмия и необходимой степени откачки реактора.
В атмосфере реактора неизбежно будет присутствовать кислород, который будет окислять вещества, участвующие в реакции. Рассмотрим окисление кадмия:
Cd(тв) + 0.5 O2(г) = CdO(тв)
Константа равновесия для этой реакции:
КР = ΔGT/RT = (1/РО21/2)равн
ΔGT = -RTln(Kp)реал + RTln(Kp)равн
ΔGT = -RTln(1/РО21/2)равн + RTln(1/РО21/2)реал
ΔGT = 0,5RTln(PO2)равн – 0.5RTln(PO2)реальн
Поскольку процесс окисления нежелателен, будем искать условия при которых процесс будет термодинамически невыгоден, то есть изменение свободной энергии Гиббса положительно.
ΔGT > 0
Выполняется, если (PO2)равн > (PO2)реальн
Расчет:
На основании закона Гесса рассчитаем стандартную энтальпию процесса ΔHo298:
ΔHo298=Σνi ΔHof,298(кон)- Σνi ΔHof,298(исх), где νi-число молей вещества.
ΔHo298= ΔHof,298 (CdОтв)-(ΔHof,298 (Cdтв)+ ΔHof,298 (О2г)) = -256,1 кДж
Расчитаем стандартную энтропию процесса ΔSo298:
ΔSo298 = Σνi ΔSo298(кон)- Σνi ΔSof,298(исх)
ΔSo298 = ΔSo298 (CdОтв)-(ΔSo298 (Cdтв)+ ΔSo298 (О2г)) = 54,8-51,76-0,5∙205,03 = -99,475 Дж/К
Свободная энергия Гиббса:
ΔGo298 = ΔHo298 – 298ΔSo298
ΔGo298 = -256100 + 298∙99,475 = -226,456 кДж
lg(Kp) = - ΔGo298/(298Rln(10)) = 226456,4/(298∙8,31∙ln10) = 39,715
ΔGo800 = ΔHo298 – 800ΔSo298 + 298∫800ΔCpodT – 800298∫800(ΔCpo/T)dT = -256100 + 800∙99,475 + 2,805∙(800-298) - 800∙2,805∙ln(800/298) = -177,328 кДж
lg(Kp) = - ΔGo800/(800Rln(10)) = 11,584
| T,K | ∆G0,кДж/моль | lgKp |
| -226,456 | 39,715 | |
| -177,328 | 11,584 |

Окисления кадмия избежать невозможно, рекомендуется откачать воздух до минимально возможного, т.к. малое количество кислорода не сможет сильно окислить кадмий.
Выводы
1. Процесс получения сульфида кадмия n-типа электропроводности путем выращивания эпитаксиальных слоев из газообразных компонентов возможен с точки зрения термодинамики при предлагаемых условиях проведения процесса:
TCd = 847 К
TTe2 = 625К
TCdTe = 1200 К
В качестве рекомендаций можно предложить откачать ампулу реактора до максимального высокого вакуума, не использовать нижние слои полупроводникового соединения.
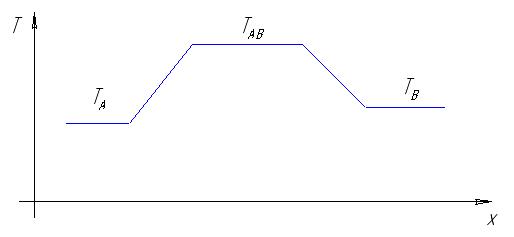
Приведем принципиальную схему реактора и приблизительное распределение температур:
|
|
|
|
|
|
|
|
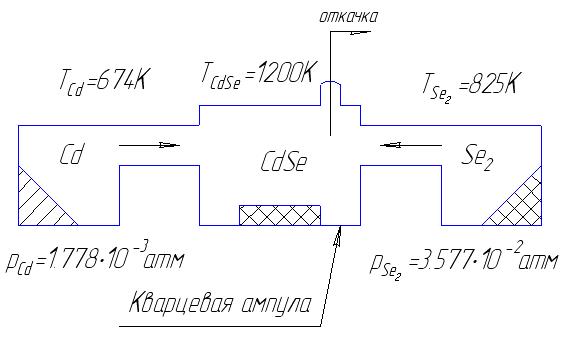
Рис. 4.1. Принциапиальная схема реактора с тремя температурно независимыми зонами: A – для подогрева и испарения Cd, B – для подогрева и испарения Te2, AB – для синтеза CdTe.
|
|
|


Список использованной литературы
1. Горелик С.С., Дашевский М.Я., «Материаловедение полупроводников и диэлектриков», Москва: Издательство МИСИС, 2003
2. Луцкая О.Ф., Чеснокова Д.Б., Максимов А.И., «Химические и фазовые равновесия в технологии материалов электронной техники», СПб.: Издательство СПбГЭТУ "ЛЭТИ", 2005
 Температура плавления соединения CdTe соответствует 1092 °С. Максимум на кривой ликвидус смещен в сторону избытка теллура относительно стехиометрического состава на 4- 10 4 % (ат.). Соединение CdTe имеет узкую область гомогенности: при 727 °С она простирается на 2- 10-4 % (ат.) как в сторону избытка Cd, так и в сторону избытка Те.
Температура плавления соединения CdTe соответствует 1092 °С. Максимум на кривой ликвидус смещен в сторону избытка теллура относительно стехиометрического состава на 4- 10 4 % (ат.). Соединение CdTe имеет узкую область гомогенности: при 727 °С она простирается на 2- 10-4 % (ат.) как в сторону избытка Cd, так и в сторону избытка Те.
Вырожденные эвтектики со стороны Cd и Те имеют температуру плавления чистых металлов. Результаты термодинамических расчетов фазовых равновесий в системе Cd—Те находятся в хорошем согласии с экспериментальными данными.
Температура плавления CdTe понижается с увеличением давления. Соединение CdTe может существовать в двух модификациях: в структуре типа вюртцита и сфалерита.
