Геометрические характеристики поперечных сечений стержней.

Геометрические характеристики поперечных сечений стержней.

Основные определения и формулы.

 

Основными геометрическими характеристиками поперечных сечений стержней, (рис.1.1) используемыми при расчете стержней на прочность, являются следующие.

Площадь сечения F.

Статические моменты сечения относительно осей Оx и Oy

, . (1.1)

Осевые моменты инерции

, . (1.2)

Центробежный момент инерции

Рис.1.1

. (1.3)

Полярный момент инерции

. (1.4)

Статические моменты имеют размерность длины в третьей степени (см³), а моменты инерции – единицы длины в четвертой степени (см⁴).

Координаты центра тяжести сечения определяются по формулам

, . (1.5)

Оси, проходящие через центр тяжести сечения, называются центральными осями. Статический момент сечения относительно любой центральной оси равен нулю.

При определении моментов инерции сечений используются зависимости между моментами инерции при параллельном переносе осей координат (рис.1.2):

(1.6)

где а и b – координаты центра тяжести О в системе координат О ₁ х ₁ y ₁.

	Рис.1.2

Две взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции. Осевые моменты инерции относительно главных осей имеют экстремальные значения J_max = J ₁ и J_min = J ₂. Они называются главными моментами инерции.

Если главные оси проходят через центр тяжести сечения, то они называются главными центральными осями сечения.

Величины главных моментов инерции J ₁ и J ₂ и углы наклона главных осей a₁ и a₂ к оси Ох определяются по формулам

(1.7)

Ось симметрии сечения и любая ось, ей перпендикулярная, составляют пару главных осей. Для сечений, имеющих более двух осей симметрии, все центральные оси являются главными.

Ниже приведены справочные данные о геометрических характеристиках простых сечений.

 

 

Рис.1.3 Рис.1.4

Прямоугольник (рис.1.3)

, , , . (1.8)

Равнобедренный треугольник (рис.1.4)

, . (1.9)

 

 

 

Рис.1.5 Рис.1.6

Круг (рис.1.5)

, . (1.10)

Полукруг (рис.1.6)

, , . (1.11)

Геометрические характеристики сечений прокатных стержней (двутавра, швеллера, уголка) приведены в сортаменте.

 

 

Решение задач

 

Задача 1.1.

Определим моменты инерции относительно главных центральных осей сечения в виде прямоугольника с круглыми отверстиями (рис.1.7).

Размеры сечений на рисунках 1.7 ¸ 1.12 даны в сантиметрах.

Оси симметрии Ох, Оу являются главными центральными осями всего сечения.

Моменты инерции и площади прямоугольника и круговых вырезов относительно их собственных центральных осей определяются по формулам (1.8) и (1.10).

Рис.1.7

,

;

.

Моменты инерции сечения относительно главных центральных осей определяются по формулам (1.6).

;

.

Задача 1.2.

Определим моменты инерции относительно главных центральных осей поперечного сечения, показанного на рис.1.8.

Разобьем сечение на три простые фигуры: прямоугольник с размерами 12´8 см и два равнобедренных треугольника с размерами 12´6 см. Моменты инерции и площади прямоугольника и треугольников относительно их собственных центральных осей определяются по формулам (1.8) и (1.9).

, ,

;

Рис.1.8

, ,

.

Площадь всего сечения равна

.

Моменты инерции сечения относительно главных центральных осей Ох, Оу определяются по формулам (1.6).

;

.

 

 

Задача 1.3.

Определим моменты инерции относительно главных центральных осей поперечного сечения стального стержня, составленного из четырех равнобоких уголков L100´100´10 и листа сечением 300´10 мм (рис.1.9).

Выпишем из сортамента площадь и моменты инерции сечения уголка относительно собственных центральных осей О ₁ х ₁ и О ₁ у ₁:

, F ₁ = 19,2 см² .

Моменты инерции относительно осей Ох и Оу и площадь сечения листа равны

, , F ₂ = 30 см².

Площадь всего сечения равна

F = 4×19,2 + 30 = 106,8 см².

Моменты инерции сечения относительно главных центральных осей Ох и Оу определяются по формулам (1.6).

Рис.1.9

Задача 1.4.

Определим положение центра тяжести и моменты инерции относительно главных центральных осей поперечного сечения чугунной балки (рис.1.10).

Данное сечение можно рассматривать как прямоугольник с размерами 24´18 см и прямоугольный вырез с размерами 12´12 см.

Площадь сечения равна

F = 24×18 – 12×12 = 288 см².

Рис.1.10

Для определения положения центра тяжести сечения, который находится на оси симметрии Оу, в качестве вспомогательной оси выберем ось О ₁ х ₁, проходящую через нижнее основание.

 

Статический момент сечения относительно этой оси найдем как разность статических моментов двух прямоугольников

.

Определим по формуле (1.5) координату центра тяжести

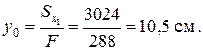
Оси Ох и Оу являются главными центральными осями сечения.

По третьей из формул (1.8) определим момент инерции сечения относительно оси О ₁ х ₁:

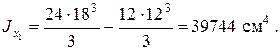
Моменты инерции сечения относительно главных центральных осей определяются по формулам (1.6).

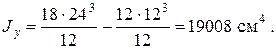
Задача 1.5.

Определим положение центра тяжести и моменты инерции относительно главных центральных осей поперечного сечения стальной балки, составленной из двух двутавров I27 и стального листа сечением 400´12 мм (рис.1.11).

Моменты инерции и площади сечений двутавра и листа относительно собственных центральных осей соответственно равны:

F ₁ = 40,2 см² ;

,

,

Рис.1.11

F ₂ = 40×1,2 = 48 см².

 

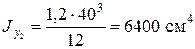Площадь всего сечения равна

F = 2×40,2 + 48 = 128,4 см².

Для определения положения центра тяжести всего сечения найдем статический момент сечения относительно оси О ₁ х ₁, проходящей через центры тяжести двутавров:

По второй из формул (1.5) получим

Оси Ох и Оу являются главными центральными осями. Моменты инерции сечения относительно этих осей равны

;

.

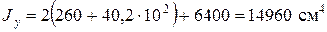Задача 1.6.

Для стержня несимметричного сечения, составленного из двутавра I50 и неравнобокого уголка L200´125´16 (рис.1.12, а), определим положение центра тяжести сечения, моменты инерции относительно главных центральных осей и положение этих осей.

 

 

Рис.1.12

моменты инерции и площади сечений двутавра и уголка относительно их собственных центральных осей соответственно равны:

F ₁ = 100 см²;

F ₂ = 49,8 см².

Площадь всего сечения равна

F = 100 + 49,8 = 149,8 см².

Для определения положения центра тяжести выберем в качестве вспомогательных осей оси двутавра О ₁ х ₁ и О ₁ у ₁. По формулам (1.5) получим

Эти величины и координаты центров тяжести двутавра и уголка в системе координат Оху показаны на рис.2.6, а и соответственно равны:

Определим по формулам (1.5) моменты инерции сечения относительно центральных осей Ох и Оу.

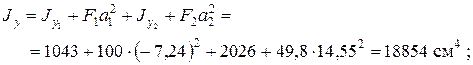
По формулам (1.7) найдем величины главных моментов инерции и углы наклона главных осей 1 и 2 к оси Ох.

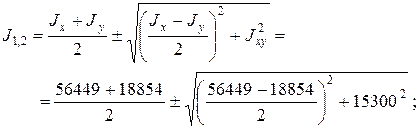
J ₁ = 61889 см⁴ , J ₂ = 13415 см⁴ ;

, ;

, .

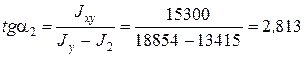На рис.1.12, б приведено графическое определение величин главных моментов инерции и положения главных осей.

 

Контрольные вопросы

1. Перечислите основные геометрические характеристики поперечных сечений стержней и напишите их выражения в интегральной форме.

2. Относительно каких осей статические моменты сечения равны нулю?

3. Относительно каких осей сечения центробежный момент инерции равен нулю?

4. Какой зависимостью связаны между собой осевые и полярный моменты инерции?

5. Напишите формулы для координат центра тяжести сечения.

6. Напишите зависимости между моментами инерции относительно параллельных осей и объясните их смысл на простых примерах.

7. Какие оси называются главными осями инерции? Напишите формулы для определения главных моментов инерции и углов наклона главных осей.

8. Как определяется положение главных осей инерции для симметричных сечений?

9. Напишите формулы для моментов инерции прямоугольника и круга.

10. Как изменяется центробежный момент инерции прокатного уголка при изменении направлений его центральных осей, параллельных полкам?

 

Библиографический список

 

1. Г.С. Варданян, В.И. Андреев, Н. М. Атаров, А.А. Горшков. Сопротивление материалов с основами теории упругости и пластичности. М., АСВ, 1995.

2. Г.С. Варданян, Н.М. Атаров, А.А. Горшков, В.В. Павлов. Сопротивление материалов с основами строительной механики.Ч.1, М., МГСУ, 1998.

3. Н.М. Атаров, Ю.Д. Насонкин. Примеры решения задач по сопротивлению материалов. Ч.1, М., МИСИ, 1990.