Электрическая цепь с активным сопротивлением.
Пусть к зажимам цепи с активным сопротивлением R приложено напряжение источника питания
.
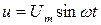, т.к. sin90 =1,то амплитуда тока в цепи:
.
Из предыдущего уравнения видно, что ток в элементе с активным сопротивлением совпадает по фазе с напряжением на этом элементе.
Так как эффективное значения напряжения и тока в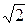 
раза меньше их максимальных значений, то аналогично можно записать 
.
На векторной диаграмме для цепи с активным сопротивлением векторы напряжения и тока совпадают по направлению.
Мгновенное значение мощности цепи синусоидального тока равно произведению мгновенных значений напряжения и тока:
р=iu
Цепь переменного тока с ёмкостью.
Если подключить конденсатор к источникупеременного тока, то процесс его заряда и разряда будет осуществляться непрерывно. Это означает, что черезёмкостьбудет проходить переменный электрический ток.
i = Imsin(ωt)
Ток i при условии включения в цепь переменного тока ёмкости будет определяется количеством электричества q, протекающего по этой цепи в единицу времени. Из этого следует, что:
где Δq – это изменение заряда q (то есть количества электричества) в течение времени Δt.
Заряд q, накоплен при изменениях напряжения u в конденсаторе, также подвержен непрерывному изменению, которое выражается формулой:
где Δu – это изменение напряжения u в течение промежутка времени Δt.
Та скорость, с которой изменяется напряжение (она выражается отношением Δu / Δt) будет иметь свои наибольшие значения тогда, когда угол ωt равняется 360°, 180° и 0°, а значит и ток i принимает max значения именно в эти моменты времени. Если же угол ωt равняется 270° и 90°, то i = 0, т.к. скорость изменения напряжения Δu / Δt = 0.
Ток заряда, который принято считать положительным, в цепи течет тогда, когда происходит заряд конденсатора, то есть на протяжение первой четверти периода. По мере того, как разница потенциалов на электродах ёмкости растет вследствие накопления ею электрического заряда, значение тока i падает. Когда ωt = 90°, наступает полный заряд емкости, значение i = 0, а разность потенциалов между электродами конденсатора обретает то же самое значение, что и напряжение источника тока.
Емкостное сопротивление.
Сопротивление, которое проявляет ёмкость к переменному току, носит название емкостного. Единицей измерения этой величины является Ом, а обозначается оно Х с.
Реактивная мощность: Q = ХС*I Вар.
Индуктивность в цепи переменного тока.
Рассмотрим график зависимости тока и ЭДС самоиндукции от времени.
ЭДС самоиндукциипрямо пропорциональна и противоположна по знаку скорости изменения тока:
График демонстрирует эту зависимость. 
Между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.
Аналогично между точками 2 и 3 — ток уменьшается — скорость изменения тока отрицательная и увеличивается — ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика — там все процессы протекают по такому же принципу. Кроме того, на графике видно, что при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: eL < 0, i > 0, участок 3-4: eL > 0, i < 0. Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены «навстречу» току источника). А на участках 2-3 и 4-5 все наоборот — ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока). И в итоге мы приходим к очень интересному факту — катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:
XL = ωL Ом
Где:L— индуктивность;ω — круговая частота: ω = 2πf, f — это частота переменного тока.
. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. По 2-му закону Кирхгофа:
u + eL = 0.
Следовательно: u = - eL. Построим на одном графике зависимости тока и напряжения в цепи от времени:
Ток и напряжение сдвинуты по фазе друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности.
При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на π/2.
i = Imsinωt
u = Umsin(ωt+π/2)
ω = 2fπ
Реактивная мощность:Q = XL*I2 Вар